8337

3

УДК: 519.2 (076.5)

Филатов Л.В. Аналитические и численные методы решения уравнений математической физики: учеб. - метод. пос. / Л.В. Филатов; Нижегородский государственный архитектурно - строительный университет. – Нижний Новгород: ННГАСУ, 2022. – 51 с. ил.– Текст: электронный

Рассматривается основные методы решения уравнений математической физики. На примере уравнения теплопроводности излагается метод Фурье аналитического решения в виде функциональных рядов. Даются представление о приближенных проекционных методах Галеркина, Ритца и методе конечных элементов. Приводятся основы конечноразностного метода численного решения начально-краевых задач. Даются примеры решения задач, набор расчетных заданий и контрольных вопросов для самопроверки материала.

Пособие предназначено обучающимся в ННГАСУ для подготовки к лекционным и практическим занятиям по дисциплине «Аналитические и численные методы решения уравнений математической физики» по научным специальностям 2.1.3

Теплоснабжение, вентиляция, кондиционирование воздуха, газоснабжение и освещение; 2.1.6 Гидротехническое строительство, гидравлика и инженерная гидрология.

© Л.В. Филатов, 2022 © ННГАСУ, 2022.

4

Введение

Для исследования реальных физических объектов и/или их систем различных пространственно-временных масштабов строятся математические модели, отражающие основные наблюдаемые свойства объектов, интересующих исследователя. Состояние системы в модели описывается координатными функциями сосредоточенными X k X k (t) или распределенными

Uk Uk (t, x, y, z) .

В динамических моделях координаты однозначно задают состояние системы, а в стохастических и квантовых случайно и являются случайными функциями. В динамических моделях основные законы изменения состояний объектов представляют собой конечные связи или дифференциальные уравнения

для дискретных (сосредоточенных) систем объектов и

для непрерывных (распределенных) систем объектов.

Количество координат определяет количество степеней свободы в модели, а количество пространственных координат распределенной системы размерность модели, так одномерная модель содержит только координату х, двухмерная x,y, а трехмерные модели x,y,z. Стационарные модели не исследуют изменения распределенных систем во времени, поэтому переменная t в них отсутствует.

Решение дифференциальных уравнений в обыкновенных производных для дискретных моделей и дифференциальных уравнений в частных производных не однозначно и зависит от произвольных констант или произвольных функций. Для нахождения единственного решения, соответствующего реальности, система уравнений модели должна быть дополнена дополнительными соотношениями, это начальными условиями и краевыми условиями для распределенных моделей.

Математическая физика имеет своим предметом решение и анализ уравнений распределенных моделей. Уравнения математической физики (УМФ) по своим качественным свойствам подразделяются на гиперболические (процессы колебаний и распространения волн), параболические (процессы диффузии и эволюции возмущений) и эллиптические (стационарные равновесные состояния). Задачи решения УМФ сложны как с точки зрения существования и единственности решения, так и его нахождения в той или иной форме. Существует не много методов решения и задач, допускающих получить решение в аналитической форме. Метод характеристик позволяет

5

находить решения в конечной форме, методы потенциалов и функций Грина дают решение в интегральном виде, метод Фурье представляет решение в виде функциональных рядов. Все эти классические методы позволяют решать и анализировать достаточно простые (модельные) уравнения. Для решения достаточно сложных задач имитационного моделирования на сегодня доступны методы численного решения.

В данном пособии рассматриваются задачи теплопроводности аналитическим методом Фурье и численными проекционно-сеточными методами.

I. Аналитические методы решения уравнений математической физики

Известно, что теплопередача осуществляется при помощи конвекции, теплопроводности и теплового излучения. Рассмотрим задачу о теплопроводности твердого тела.

Температура в каждый момент t в твердом теле V в каждой его точке M описывается координатной функцией u(t,M). Пусть dV малый элемент тела в окрестности точки М. При наличии источников тепла в этот элемент за время dt поступит тепло dQ1 F (M ,t)dVdt . Через границу этого элемента за счет

теплопроводности согласно закона Фурье уйдет тепло в соседние элементы

/ c a2 , F / c f (t, M ) и тогда процесс распределения тепла во времени по телу путем теплопроводности описывается уравнением

u a2 u f (t, M ) ,

t

6

Физически ясно, что решение уравнения должно быть единственным, но решения уравнения теплопроводности многозначны. Поэтому для единственности необходимо дополнить задачу начальными и граничными условиями.

пространством если:

- H – линейное пространство над полем действительных чисел R ( , ) . Т.е

1 f (x) 2 g(x) 3h(x) ... H , i R

- В пространстве Н введена операция скалярного умножения f (x), g(x) H

( f , g) R

такое что: ( f , g) (g, f ) ; ( f , g) ( f , g) R ; ( f g, h) ( f , h) (g, h);

( f , f ) 0 ; ( f , f ) 0 f 0 .

- В пространстве Н определена норма элементов f ( f , f ) или f 2 ( f , f ) .

f g r 0 называется расстоянием между элементами f и g .

8

n

Таким образом, fn ck k (x) Vn является ортогональной проекцией функции

k 1

на подпространство так как ( n , k ) 0, k n .

Подставив коэффициенты Фурье в выражение для n2 и учитывая что

i 1

функции. Вопрос к чему он сходится? Он может сходиться к другой функции в или вне H 2 [a, b].

Бесконечный базис i (x) называется полным в H 2 [a, b] , если для любой функции ее ряд Фурье сходиться к ней, то есть любая функция представима

теоремы Дирихле, любая кусочно-непрерывная и ограниченная функция

f (x) может быть однозначно разложена на симметричном интервале ( l l) в ряд Фурье

9

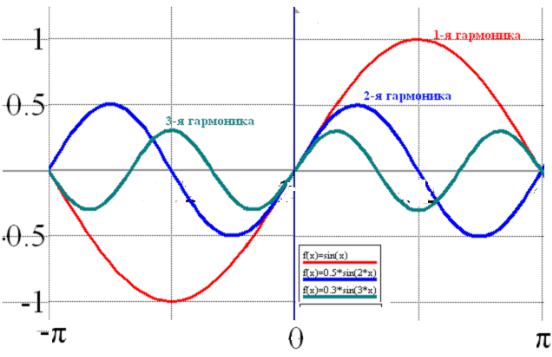
В частности, нечетные на ( ) функций разлагаются в ряд по системе функций sin kx

Кроме того, если взять любую линейно-независимую систему функций, то ее всегда можно привести к ортогональной. Действительно, пустьyi (x) линейно-независимая система. Тогда процесс ортогонализации Грамма-

Шмитта таков:

z1 y1

…………………………………………………………………………………………

степенных рядах Тейлора-Маклорена. Ортогонализируем ее.

…………………………………………………………………………………………

Полученные на отрезке [-1;1] ортогональные с весом (x) 1 многочлены

многочленов