8118

Из полученных эпюр Qx и Qy компонуется пространственная эпюра Q, а из эпюр Mx и

My - пространственная эпюра Mи.

Таким образом, все четыре эпюры: N, Mк, Q, Mи построены. Они содержат полную информацию об изменениях усилий N, Qx , Qy , Mx, My, Mz по длине стержня.

4.2 Косой (сложный) изгиб

Косым изгибом называется такой случай изгиба, при котором плоскость действия нагрузки не совпадает ни с одной из главных осей инерции сечения (рис.4.5). Рассмотрим случай, когда к сечению бруса под некоторым углом приложена сила P.

Рис. 4.5

При решении таких задач силу Р раскладывают на составляющие Рх и Ру и затем пользуются принципом независимости действия сил:

Изгибающие моменты в сечении 1-1:

Нормальные напряжения в общем случае:

(4.1)

Очевидно, что можно найти такую линию, на которой суммарные напряжения σ равны нулю. Такая линия называется нейтральной (или нулевой), текущие координаты x и y:

(4.2)

(4.3)

где φ – угол между направлением действия силы и осью Х.

Из этих формул следует, что нейтральная линия в сечении, в общем случае, не пер-

пендикулярна следу плоскости действия в том же сечении результирующего изгибающего момента. Эти линии будут перпендикулярны при условии равенства углов α и φ. А это возможно в следующих случаях: α=0, то есть Мy=0, α=π/2, то есть Мx=0,

т.е. когда Ix = Iy угол между силовой и нулевой линией прямой, а это значит, что любая

центральная ось сечения является главной осью ,значит, изгиб будет прямым.

Для таких сечений, у которых центральные оси главные (квадрат ,круг и т.п.), косой изгиб

невозможен.

Нейтральная линия делит поперечное сечение на две области: растянутую и сжа-

тую. Проводя линии, параллельные нейтральной и касательной к контуру поперечного сечения, находим в той и другой области наиболее удалённые от нейтральной линии точки О1 и О2 с наибольшими растягивающими и сжимающими напряжениями (рис. 4.6):

Рис. 4.6

Определим напряжение в одной из точек

(4.4)

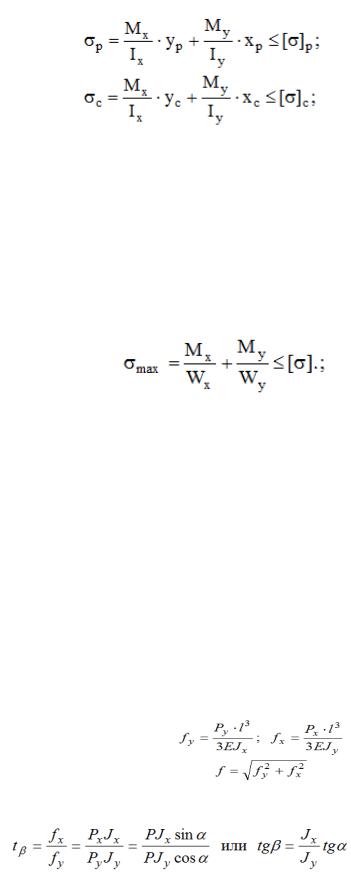
Условия прочности при косом изгибе

Для сечения произвольной формы

(4.5)

где yp и xp – координаты точки контура сечения наиболее удаленной от нулевой ли-

нии в области растяжения (опасная точка в области растяжения);

yс и xс – координаты точки контура сечения наиболее удаленной от нулевой ли-

нии в области сжатия (опасная точка в области сжатия);

[σ]p и [σ]с – допускаемые напряжения на растяжение и сжатие. - для сечений типа прямоугольник, двутавр, швеллер

(4.6)

- для круглого поперечного сечения косого изгиба не существует, расчет производим по формулам прямого поперечного изгиба:

где ось Х’ – главная центральная ось круглого сечения, перпендикулярная направле-

нию действия силы.

Перемещения и расчет на жесткость при косом изгибе

Определим прогибы при косом изгибе. Прогибы определяются отдельно от состав-

ляющих Рх и Ру, затем определяется общее перемещение:

(4.8)

Определим направление суммарного перемещения:

(4.8)

Если проанализировать формулы (4.8) и (4.3), то можно отметить ,что направление

прогибов перпендикулярно к нулевой линии и вместе с тем направление прогибов не совпадает с направлением действующей силы. Если нагрузка представляет плоскую сис-

тему сил, то ось изогнутого бруса лежит в плоскости, которая не совпадает с плоскостью действующих сил. Поэтому изгиб и называется косым.

где fmax – максимальный прогиб в балке, определяется с эпюры прогибов; [f] – допускаемый прогиб, определяется из нормативной литературы.

4.3 Внецентренное растяжение-сжатие

Вторым практически важным случаем сложения деформаций от изгиба и от продоль-

ных сил является так называемое внецентренное сжатие или растяжение, вызываемое одни-

ми продольными силами. Этот вид нагружения довольно распространен в технике, так как в реальной ситуации почти невозможно приложить растягивающую нагрузку точно в центре тяжести.

Внецентренным растяжением-сжатием называется случай, когда равнодейст-

вующая сил, приложенных к отброшенной части стержня, направлена параллельно оси стержня, но не совпадает с этой осью (рис.4.7).

Рис.4.7

Внецентренное растяжение (сжатие) испытывают короткие стержни. Все сечения яв-

ляются равноопасными, поэтому нет необходимости в построении эпюр внутренних силовых факторов.

Представим, что после проведения разреза равнодействующая Р сил действующих на отброшенную часть и приложенная к оставшейся проходит через точку с координатами (xp; yp) в главных центральных осях поперечного сечения (рис. 4.8).

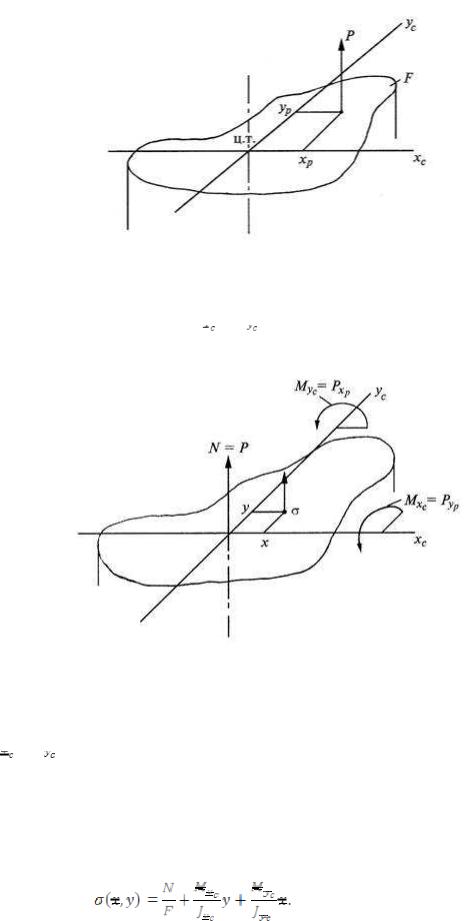
Рис.4.8

Приведем силу Р в центр тяжести сечения, т.е. направим вдоль оси стержня (сила N).

При этом появятся две пары сил относительно главных центральных осей

(рис.4.9).

Рис.4.9

Таким образом, в поперечном сечении стержня при внецентренном растяжении и сжатии возникают три внутренних силовых фактора: нормальная сила N и два изгибающих момента относительно главных центральных осей поперечного сечения.

Для вычисления нормального напряжения в поперечном сечении в окрестности точки с произвольными координатами x,y воспользуемся принципом независимости действия сил.

Будем вычислять нормальное напряжение от каждого внутреннего силового фактора в от-

дельности и результат сложим.

4.10

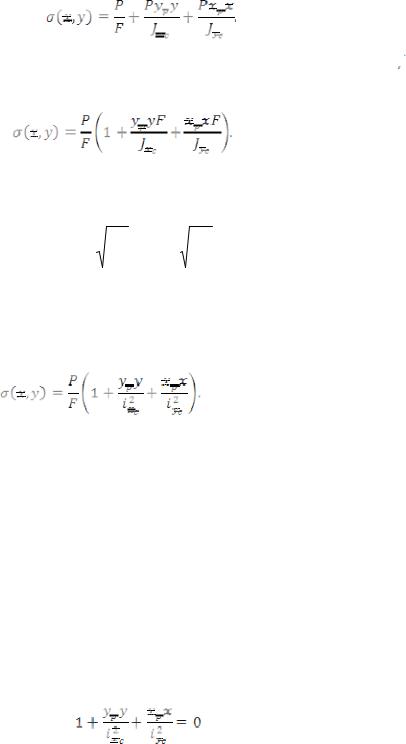
где F – площадь поперечного сечения.

По этой формуле можно вычислять нормальные напряжения в точках поперечного сечения стержня при совместном действии осевой силы и двух изгибающих моментов. В

нашем случае все три внутренних силовых фактора зависят от внецентренно приложенной силы Р (рис.4.8). Подставив соответствующие выражения в (4.10), получим

Вынесем величину нормального напряжения при осевом растяжении за

скобки

(4.11)

Введем геометрическую характеристику – радиус инерции относительно центральных

осей:

Применив (4.12) в выражении (4.11) получим

(4.13)

Мы получили формулу нормальных напряжений в поперечном сечении при внецен-

тренном растяжении или сжатии. Если сила растягивающая, то перед скобкой ставится знак плюс, если сила сжимающая, то ставится – минус.

В этой формуле координаты точки, где определяются напряжения входят в первой степени. Следовательно, если величины напряжений откладывать в масштабе в виде аппли-

кат перпендикулярно плоскости поперечного сечения, то концы этих отрезков будут лежать на плоскости, наклоненной к плоскости поперечного сечения. Будем называть эту плоскость

плоскостью напряжений. Известно, что две наклоненные плоскости пересекаются по линии.

В нашем случае в точках этой линии - это нулевая линия, которая описывается уравне-

нием

(4.14)

Анализируя (4.14) можно сделать вывод, что нейтральная линия при внецентренном растяжении и сжатии не проходит через центр тяжести, а отсекает на главных центральных осях отрезки и . Полагая последовательно в (4.14) x=0 и y=0, получим

(4.15)

Из формул (4.15) следуют некоторые закономерности, связывающие положения по-

люса (т. е. точки приложения силы) и нейтральной линии, которые удобно использовать для анализа решения задачи. Перечислим самые важные из этих закономерностей:

- нейтральная линия всегда расположена в квадранте, противоположном тому, в кото-

ром находится полюс (рис. 4.10);

-если полюс находится на одной из главных осей, то нейтральная линия перпендикулярна этой оси;

-если полюс приближается к центру тяжести сечения, то нейтральная линия удаляется от него.

-если полюс движется по прямой линии, то нейтральная линия поворачивается вокруг неподвижной точки.

Рис.4.10

Для сечений со сложным контуром знание положения нулевой линии очень важно.

Вспоминая про понятие плоскость напряжений, можно утверждать, что наибольшие по ве-

личине нормальные напряжения возникают в точках поперечного сечения наиболее удален-

ных от нулевой линии. Если взглянуть на плоскость напряжений вдоль нулевой линии, то

она будет видна в виде линии соединяющей аппликаты напряжений, то есть в виде эпюры напряжений, отложенной от линии перпендикулярной нулевой линии (рис.4.10).

Наибольшее растягивающее нормальное напряжение возникает в точке А

(4.16)

а наибольшее сжимающее нормальное напряжение возникает в точке В

(4.17)

Таким образом, при внецентренном растяжении кроме растягивающих нормальных напряжений в поперечном сечении могут возникнуть и сжимающие. При внецентренном сжатии – наоборот.

Если материал стержня одинаково сопротивляется растяжению и сжатию, то условие прочности получает такой вид:

(4.18)

Хрупкий материал обладает различными свойствами в условиях растяжения и сжатия

– плохо сопротивляется растяжению и хорошо сжатию, условия прочности составляют для двух точек: где действуют максимальные растягивающие (т. A) и максимальные сжимающие

(т. B) напряжения:

(4.19)

Для поперечных сечений с выступающими углами, у которых обе главные оси инер-

ции являются осями симметрии (прямоугольник, двутавр и др.) и . По-

этому формула упрощается, и мы имеем

(4.20)

Если же материал стержня неодинаково сопротивляется растяжению и сжатию, то не-

обходимо проверить прочность стержня как в растянутой, так и в сжатой зонах.

Задача 4.3

Чугунный короткий стержень, поперечное сечение которого изображено на рис. 4.11,

а = 3 cм, b = 2 см, сжимается продольной силой Р, приложенной в точке А. Допускаемые нормальные напряжения: на сжатие ; на растяжение[σ p ]= 30 МПа

Рис.4.11

Требуется:

1)вычислить наибольшее растягивающее и наибольшее сжимающее напряжения в поперечном сечении, выразив величины этих напряжений через Р и размеры сечения;

2)найти допускаемую нагрузку (Р) при заданных размерах сечения и допускаемых напряжениях чугуна на сжатие и на растяжение .

Решение.

Нормальное напряжение в произвольной точке сечения стержня, определяемой коор-

динатами х и у, запишется в виде

где хр, ур - координаты точки приложения силы Р (точки A); F -площадь поперечного

сечения стержня; Jxc, Jyc - главные моменты инерции сечения.

1. Определим координаты центра тяжести сечения хс и ус. Для этого выведем вспомо-

элементарным фигурам, на которые разбито заданное составное сечение (рис. 4.12). Отметим также, что площадь первой фигуры следует брать со знаком минус.

Рис. 4.12

Подставляя исходные данные, получим:

Тогда

Ввиду симметрии сечения у = 2b = 4 см. Через найденный центр тяжести проводим главные центральные оси хс и ус.

2. Вычислим главные моменты инерции.

Ввиду совпадения осей хс и хс1, хс2, хс3:

Для вычисления момента инерции относительно оси ус используем формулу измене-

ния момента инерции при параллельном переносе осей:

Здесь через l1, l2, l3 обозначены: соответственно расстояния между осью ус и осями ус1,

ус2, ус3.

3. Нахождение наибольших напряжений и допускаемых нагрузок.

Подставляя в формулу (10) вычисленные значения моментов инерции, а также коор-

динаты точки приложения нагрузки и точек, где возникают наибольшие растягивающие и сжимающие напряжения, получим:

В точке А(-4,136; 4) - напряжение сжатия

Из условия прочности при сжатии