
6267
.pdf
30
Кинетический момент вращающегося тела относительно оси вращения равен произведению осевого момента инерции на угловую скорость:
Kz = Iz ω.
Теорема об изменении кинетического момента
Производная по времени от кинетического момента механической системы относительного некоторого центра или оси равна главному
моменту внешних сил относительно этого же центра или момента: |
|
gh @ e Aв , |
|
|
AB |
или в проекциях на оси:
dKx
dt
dK y
dt
dKz
dt
n |
R |
= ∑ mx (Fke ) |
|
k =1 |
|
n |
R |
= ∑ my (Fke ). |
|
k =1 |
|
n |
R |
= ∑ mz (Fke ) k =1
Внутренние силы не могут изменить кинетический момент механической системы.
Следствие 1.
Если главный момент внешних сил механической системы относительно некоторого центра все время равен нулю, то кинетический
момент системы относительно этого центра остается неизменным.
Следствие 2.
Если главный момент внешних сил относительно какой-либо оси все время равен нулю, то кинетический момент системы относительно этой оси остается неизменным.
Дифференциальное уравнение вращательного движения
Предположим, что материальное тело вращается вокруг оси z . Его кинетический момент будет равен Kz = Izω и тогда в соответствии с теоремой об
изменении кинетического момента
d [I zω] |
|
∑ |
|
z ( |
k ) |
|
|
= |
|
m |
|
F |
. |
dt |
k =1 |
|
||||
|
|
|
|
|
||

31
Если тело в процессе вращения не изменяется, то Iz = const и мы получаем
дифференциальное уравнение вращательного движения твердого тела:
|
dω |
n |
R |
R |
|
I z |
|
= ∑ mz (F ek ) , |
|||
dt |
|||||
|
k =1 |
|
|
||
Если учесть, что dω = ε = ϕ&& , это уравнение можно записать в виде
dt
n |
R |
R |
или |
Izϕ |
n |
R |
R |
|
|
|
|
||||
Izε = ∑ mz (F k ) , |
= ∑ mz (F k ) . |
||||||
|
|
e |
|
&& |
|
|
e |
|
|
|
|
|
|
|
|
k =1 |
|
|
|
|
k =1 |
|
|
При поступательном движении мерой инертности тела является его масса, а при вращательном − его момент инерции.
Задача 2.9.
Однородный стержень длиной k и массой вращается относительно оси, проходящей через его конец О перпендикулярно ему с угловой скоростью ; и с угловым ускорением Q.
Найти кинетический момент стержня относительно оси вращения.
O |
ω |
|
ε
K − ?
Решение.
Кинетический момент твердого вращающегося тела вычисляется по
формуле: |
Im − |
момент инерции относительно оси вращения, ω − |
|
||
Km Imω, где |
угловая |
||||
скорость вращения. |
|
|
|
|
|
Ось вращения для стержня не является центральной осью, поэтому момент |
|||||
инерции Im находим по теореме Гюйгенса: |
|
||||
Im ImС m |
q |
, |
|
||
|
|
||||
где ImС ml |
⁄12 |
− |
момент инерции однородного тонкого |
стержня |
|
относительно оси, проходящей через его середину.

32
Тогда Im ml m 6q7 s ml .
Находим кинетический момент:
Km Imω s ml ∙ ω.
Задача 2.10.
Регулятор Уатта в установившемся движении при угловой скорости вращения ω 12 с1 имеет момент инерции I 40 кгм . Сопротивлением вращению пренебречь.
Найти момент инерции I при новом значении угловой скорости ω 3 с1 при условии сохранения кинетического момента.
ω
Решение.
Кинетический момент твердого вращающегося тела вычисляется по
формуле: |
Km Imω, |
|
где Im |
− |
момент инерции относительно оси вращения, |
ω |
− |
угловая скорость вращения. |
При сохранении кинетического момента справедливо равенство
I ∙ ω I ∙ ω ,
откуда следует, что I I ∙ ω⁄ω 40 ∙ 12⁄3 160 кг ∙ м .
Задача 2.11.
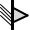
Однородный диск радиуса R и массой m вращается вокруг неподвижной оси, проходящей через точку О и перпендикулярной плоскости диска, с угловой скоростью ω и угловым ускорением ε.
Определить, чему равен кинетический момент диска относительно оси вращения.

33
R
ε 
C
 O
O
ω 
Решение.
Кинетический момент твердого вращающегося тела вычисляется по формуле: Km Imω,
где Im − момент инерции относительно оси вращения, ω − угловая скорость вращения.
Ось вращения для диска не является центральной осью, поэтому момент |
|||
инерции Im находим по теореме Гюйгенса: |
|||
|
Im ImС mR |
, |
|
где |
ImС mR ⁄2 |
− |
момент инерции круглого однородного диска |
относительно центральной оси. |
|||
Тогда |
Im ImС mR |
mR mR s mR . |
|
Находим кинетический момент:
Km Imω s mR ∙ ω.
2.6. Работа силы
Рассмотрим отрезок траектории точки M, в которой приложена сила F. Элементарная работа силы равна скалярному произведению вектора
силы F и вектора элементарного перемещения точки ее приложения dr :
δA = (F·dr). |
(2.2) |
Представив F и dr в виде:
F = Xi + Yj + Zk, dr = dxi + dyj +dzk,
получим аналитическое выражение элементарной работы силы, соответствующее не векторному, а координатному способу задания движения точки приложения силы:

34
δA = Xdx + Ydy + Zdz.
Eсли известен естественный способ задания движения точки M и дан закон изменения ее дуговой координаты s = f(t) , то формулу (2.2) можно записать в виде:
δA = | F |·| dr |·cos (F, dr) = F·ds, |
(2.3) |
τ |
|
где Fτ – проекция силы F на направление орта касательной τ.
В случае, когда точка приложения силы F перемещается по прямой M1M2 на расстояние S и при этом сила остается постоянной по модулю и направлению
(рис. 9),
|
|
|
F |
|
M1 |
M |
α |
M2 |
|
|
|
|
|
|
|
|
|
|
|
Рис. 9.
из формулы (2.3) получим
w |
/ xw=/} y cos | I y cos | ~ I |
|
|
Таким образом, работа постоянной силы на прямолинейном перемещении равна произведению модуля силы на модуль перемещения и на косинус угла между направлением силы и перемещением. При этом:
A (F) > 0, если 0 < α < π/2,
A (F) = 0, если α = π/2,
A (F) < 0, если π/2 < α < π.
2.7. Кинетическая энергия
Кинетической энергией материальной точки называется величина, равная половине произведения массы точки на квадрат скорости:
T = 1 mv2
2

35
Кинетическая энергия механической системы равна сумме кинетических энергий ее точек
T = ∑n 1 mk vk 2
k =1 2
Кинетическая энергия твердого тела вычисляется по аналогичной формуле с той разницей, что сумма заменяется интегралом:
• 12 ( ,
где dm ─ масса бесконечно малого объема тела, а v ─ его скорость.
Вычисление кинетической энергии при различных формах движения
1. Поступательное движение тела
При поступательном движении тела его кинетическая энергия равна
• 12 €
2. Вращательное движение тела
При вращении тела относительно некоторой оси z его кинетическая энергия
равна
• 12 •‚; .
3. Плоскопараллельное движение тела
При плоском движении тела кинетическая энергия вычисляется с помощью теоремы Кенига:
Кинетическая энергия механической системы равна сумме кинетической энергии поступательной части движения и кинетической энергии системы в ее относительном движении относительно центра масс. €.
Относительное движение тела относительно центра масс является вращательным, поэтому его кинетическая энергия равна •‚С; .
В результате получаем, что
•пл € •‚€; ,
36
где € скорость центра массы тела, а •‚€ момент инерции тела
относительно оси, проходящей через центр масс тела перпендикулярно оси вращения.
2.8. Теорема об изменении кинетической энергии механической системы Теорема об изменении кинетической энергии в дифференциальной форме
Производная по времени от кинетической энергии механической системы
равна сумме мощностей всех действующих в системе сил:
ƒ ∑AB „A
или, после разделения мощностей внешних и внутренних сил:
ƒ ∑AB „A… ∑AB „A[
Для неизменяемых систем, у которых внутренние силы не работают, получим:
ƒ ∑AB „A…
Теорема об изменении кинетической энергии в интегральной форме
Изменение кинетической энергии механической системы за некоторый
промежуток времени равно сумме работ всех действующих в системе сил: |
||
• • ∑AB wA |
(2.4) |
|
или, выделяя отдельно работы внешних и внутренних сил: |
||
• • ∑AB w…A ∑AB |
w[A |
|
где T0 ─ начальное, а T ─ конечное значение кинетической энергии. |
||
Для неизменяемых систем |
†∑bBc Aˆb 0 ‰ можно записать: |
|
T T ∑cbB A‹b
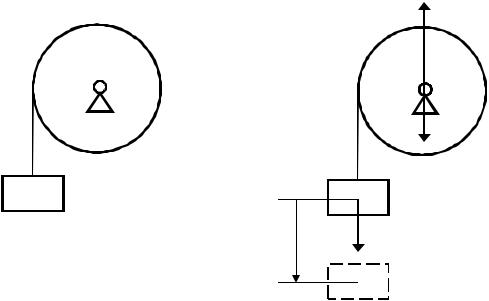
Задача 2.12. Найти ускорение тела A, принимая барабан B за однородный цилиндр и полагая mA = mB (рис. 10, а).
37
а) |
|
y |
б) |
|
|
|
y |
|||||||
|
|
|
||||||||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
B |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
NB |
|
|||
|
|
|
|
x |
|
|
||||||||
|
|
|
|
|
B |
|
x |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
PB
A (1)
A |
PA |
sA |
A′ (2)
Рис. 10
Решение:
Груз A движется под действием постоянной силы PA с постоянным ускорением, которое не зависит от начальной скорости, и которую можно считать равной нулю.
Рассмотрим два состояния системы: первое – в состоянии покоя, для которого T1 = 0, и второе – текущее, соответствующее смещению груза A на величину sA от первоначального положения (рис. 10, б), для которого
T2 = T = TA + TB = (1/2)mAvA2 + (1/2)(mBR2/2)(vA/R)2 = (3/4)mvA2 .
Подставляя T2 в (2.4) вместе с работой силы PA , придем к соотношению:
(3/4)mvA2 = mgsA ,
продифференцировав которое, получим: (3/2)vAaA = vAg ,
откуда aA = (2/3)g.
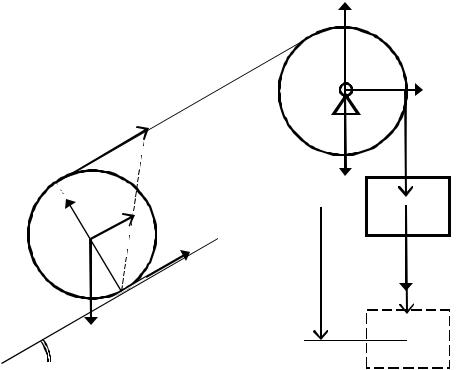
Задача 2.13.
38
Система, состоящая из трех тел A, B и C одинаковой массы приходит в движение из состояния покоя. Принимая B и C за однородные цилиндры, определить:
–какую скорость приобретет груз A , пройдя расстояние SA,
–ускорение тела A (рис. 11).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
NBX |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
NBY |
|
|
|
B |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
vC′ = vA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
vB = vA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
PB |
|
|
|
(1) |
|||
|
|
|
|
|
vC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
NС |
|
|
|
|
|
|
|
|
FС |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
sA |
|
|
|
|
PA |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
vA |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A′ |
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
PС |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 11
Решение. Прикладываем к системе внешние активные силы (PA, PB, PC) и реакции отброшенных связей (NBX, NBY , NC , FC) , где FC – сила трения, приложенная к катку C.
Воспользуемся теоремой об изменении кинетической энергии системы
(2.4):
T2 – T 1 = A12(e) + A12(i), |
(1) |
выбрав в качестве первого состояния – состояние покоя, а в качестве второго – текущее состояние, соответствующее смещению груза A на расстояние sA .
По условию задачи T1 = 0, а
T2 = TA + TB + TC = (1/2)mAvA2 + (1/2)JBωB2 + (3/4)mCvC2 .
39 |
|
Подставляя сюда |
|
ωB = (vB /RB) = (vA /RB), |
|
JB = (mB RB2)/2 и |
(2) |
vC = vC′ /2 = vA /2, |
|
и обозначая mA = mB = mC = m, получим: |
|
T2 = (15/16) m vA2. |
(3) |
Переходя к вычислению работы сил, отметим, что |
|
A12(e)(NC , FC) = 0. |
(4) |
В самом деле, точка P, в которой приложены силы NC и FC является мгновенным центром скоростей диска C, то есть
δA12(e)(NC , FC) = NC δrP + FCδrP = (NC + FC) vPdt = 0,
откуда и следует (4). Итак, справедливо следующее утверждение:
Работа сил, приложенных в точке, являющейся мгновенным центром скоростей, равна нулю.
Работа сил PB, NBY и NBX равна нулю, поскольку перемещения точек их приложения равны нулю, и таким образом, работу будут совершать только силы
PA и PC: |
|
|
|
A12(e) = A12(e)(PA, PC) = PA sA – P C sC sinα. |
(5) |
||
Чтобы выразить sC через sA , |
воспользуемся |
соотношением |
(2), |
проинтегрировав которое, получим: |
|
|
|
sC = sC′ /2 = sA /2,
откуда (5) примет вид:
A12(e) = A12(e)(PA, PC) = PA sA – P C sC sinα = mgsA(1 – 0,5sin α). |
(6) |
Подставляя (в) и (е) в (а), получим:
(15/16) vA2 = gsA(1 – 0,5sin α), |
(7) |
