
5153
.pdf
Участок CE – отрезок вертикальной прямой x = 2 при - |
3 |
£ y £ |
1 |
|
|
||
2 |
2 |
||
(см. рис. 13). При x = 2 функция z(y) = 2 y 2 + 6 y является функцией одного
переменного y . Находим производную z¢ = (2 y 2 + 6 y)′ = 4 y + 6 .
Приравнивая ее к нулю: 4 y + 6 = 0 , находим точку y = - 3 , совпадающую
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
с |
левым |
концом отрезка |
- |
3 |
; |
1 |
|
(см. |
|
рис. |
16). |
Значение |
|
функции |
||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
z(y) = 2 y 2 |
+ 6 y |
при y = - |
3 |
равно: z |
- |
3 |
|
= 2 × |
- |
3 |
2 |
+ 6 × - |
3 |
|
= -4,5 , а |
|||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
2 |
|
|
|
|
||||||
значение z(x) |
на правом конце отрезка - |
3 |
; |
1 |
, то есть при |
y = |
1 |
равно: |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2 |
|
|
|
|
|
|
2 |
|
||||||||
|
1 |
1 2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
z |
|
= 2 × |
|
+ 6 × |
|
= 3,5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Следовательно, на отрезке CE наименьшее значение равно − 4,5 , а |
||||||||||||||||||||||||||||||||||
наибольшее 3,5 , |
то есть zнаим. |
= −4,5 , |
zнаиб. |
= 3,5 . |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
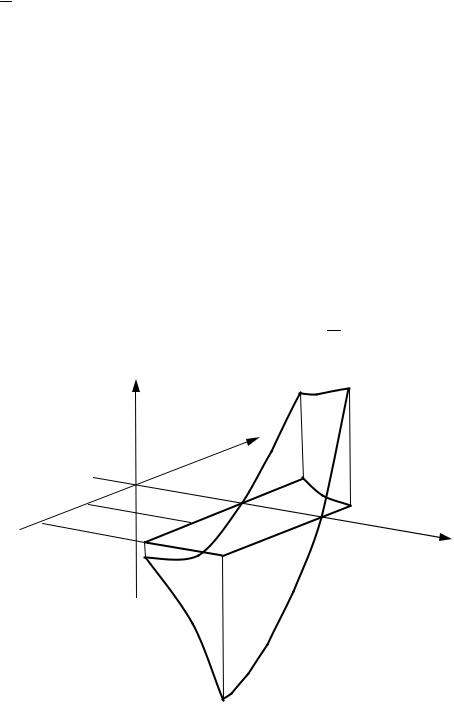
г) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В плоскости y = − |
3 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
x |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
− 4,5
Рис. 17
30
|
Участок AE – |
отрезок горизонтальной прямой y = − |
3 |
|
при 1 ≤ x ≤ 2 |
||||||||||||||||
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||
(см. рис. |
13). При |
y = - |
3 |
|
|
функция |
z(x) = - |
3x 2 |
+ |
3x |
является функцией |
||||||||||
2 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
4 |
|
|
|
|
|
||||
одного |
|
|
|
переменного |
x . |
Находим |
|
|
производную |
||||||||||||
|
|
3x |
2 |
|
3x ′ |
|
3 |
|
|
|
|
|
|
|
|
3 |
|
||||
z¢ = |
- |
|
|
+ |
|
= -3x + |
|
|
|
|
. Приравнивая ее к нулю: - 3x + |
|
|
= 0 находим |
|||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
2 |
|
|
4 |
|
4 |
|
|
|
|
|
|
|
|
4 |
|
||||
точку x = 1 , которая не принадлежит отрезку [1; 2] (см. рис. 17). Значения
4
функции z(x) на концах отрезка [1; 2] равны:
z(1) = - |
3 ×12 |
|
+ |
3 ×1 |
= - |
3 |
+ |
3 |
= - |
3 |
; |
|
|
|
||||||||
|
|
|
|
|
|
2 |
4 |
4 |
|
|
|
|||||||||||
2 |
|
|
4 |
|
|
|
|
|
|
|
|
|
||||||||||
z(2) = - |
3 × 22 |
|
+ |
3 × 2 |
= -6 + |
3 |
= -4,5 . |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
2 |
|
4 |
|
|
|
2 |
|
|
|
|
|
|
||||||||||
Следовательно, наименьшее значение z на отрезке AE равно − 4,5 , а |
||||||||||||||||||||||
наибольшее - |
3 |
, |
|
то есть zнаим. |
= −4,5 , zнаиб. |
= - |
3 |
. |
||||||||||||||
|
|
|
||||||||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
||||
3)Сравнивая полученные результаты в пунктах а), б), в), г),
имеем: z |
|
= z (2; |
1 |
) = 3,5 |
z |
|
наиб |
|
наим |
||||
|
2 |
|
|
|||
|
|
|
|
|
||
z
|
|
|
|
|
|
|
|
|
y |
− |
3 |
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
3 |
|
|
E |
|
|
|
|
|
|
|||||
|
|
1;− |
|
;− |
|
|
(1;−1;−1) |
||
|
|
2 |
|
||||||
|
|
|
|
4 |
|
|
|
||
|
|
3 |
|
|
|
2;− |
|
;−4,5 |
|
2 |
||||
|
|
|
= z (2;− 3 ) = −4,5 . 2
(1,1, 3) |
|
1 |
|
|
|
|
2; |
|
;3,5 |
|
|
|||
|
|
2 |
|
|
B
C
x
Рис. 18
31

Площадь поперечного сечения канала называют его живым сечением, а длину P = AB + BC + CD (см. рис. 19) границы такого сечения называют смоченным периметром канала. С помощью теоретических расчетов и эксперимента установлено [4], что из всех каналов с заданным живым сечением наибольшей пропускной способностью и одновременно наименьшей фильтрацией отличаются каналы с наименьшим смоченным периметром. Про такие каналы говорят,
что они имеют гидравлически наивыгоднейший профиль.
Наиболее часто сооружают каналы, а также оросительные и водосточные канавы с сечением формы равнобочной трапеции ( АВ=CD,
см. рис. 19).
A F E D
α 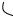
h

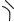 α
α
B C
Рис.19
Пример. Найти наивыгоднейший с точки зрения гидравлики профиль канала трапецеидальной формы.
Решение. Найдем размеры поперечного сечения канала заданной
площади S с наименьшим периметром P . Пусть AB = CD , |
CE ^ AD , |
||||||||
BF AD , CE = h , ÐEDC = α . Тогда |
|
||||||||
|
|
|
P = AB + BC + CD = 2 AB + BC |
(1) |
|||||
|
|
S = |
1 |
(AD + BC )× CE = |
1 |
(AD + BC )× CE |
(2) |
||
|
|
||||||||
2 |
|
2 |
|
|
|||||
CED – прямоугольный, |
|
|
|
|
|
||||
sin Ð EDC = |
CE |
или sinα = |
h |
, откуда |
|
||||
|
|
|
|||||||
|
CD |
CD |
|
||||||
32
|
|
|
|
|
|
CD = AB = |
h |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
(3) |
|||||
|
|
|
|
|
|
sinα |
|
|
|
|
|
|
|
||||||||||
Подставив (3) в (1), получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
P = |
2 h |
+ BC . |
|
|
|
|
|
|
|
(4) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
sinα |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Так как AD = AF + FE + ED , а FE = BC , |
AF = ED , находим: |
||||||||||||||||||||||
|
|
|
|
|
|
AD = 2ED + BC . |
|
|
|
|
|
|
|
(5) |
|||||||||
Из |
EDC : |
tg α = |
CE |
или tg α = |
h |
, откуда ED = |
|
h |
. Подставив |
||||||||||||||
ED |
|
|
|
|
tg α |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ED |
|
|
|
|
|
|
|||||||
последнее равенство в (5), |
находим |
AD = |
2h |
+ BC . Тогда равенство (2) |
|||||||||||||||||||
tg α |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
2h |
|
|
|
|
|
|
|
|
|
S |
|
|
h |
|
|
|||||
запишется: |
S = |
|
|
|
|
+ 2BC × h , |
откуда |
BC = |
|
- |
|
|
|
. |
Подставив |
||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
tg α |
|
|
||||
|
|
2 tg α |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
последнее равенство в (3), находим
|
P(h,α ) = |
2h |
+ |
S |
- |
h |
= |
S |
- |
2 − cos α |
× h . |
|
sin α |
|
tg α |
h |
sin α |
||||||
|
|
|
h |
|
|
|
|||||
|
Таким образом, требуется найти |
такую точку (h0 ,α 0 ) из области |
|||||||||
D = (h,α )/ 0 < α < π , h > 0 , |
|
в |
которой |
функция |
P(h,α )принимает |
||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
наименьшее значение.
Найдя частные производные функции P(h,α ) и приравняв их к нулю,
получим систему уравнений:
|
|
P¢ |
= - |
S |
- |
2 - cos α |
= 0 |
|
||||||
|
|
|
2 |
|
|
|
||||||||
|
|
|
h |
|
|
h |
|
|
|
sin α |
|
|||
|
|
|
|
|
|
|
|
|
|
. |
||||
|
|
|
|
|
2 cos α -1 |
|
|
|||||||
|
|
P¢ |
= |
= 0 |
|
|
||||||||
|
|
|
|
|
||||||||||
|
|
|
α |
|
|
sin |
2 |
α |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
Откуда cosα = |
1 |
или α0 = π = 60 , тогда |
|
|
|
|||||||||
|
|
|
|
|||||||||||
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
||
33
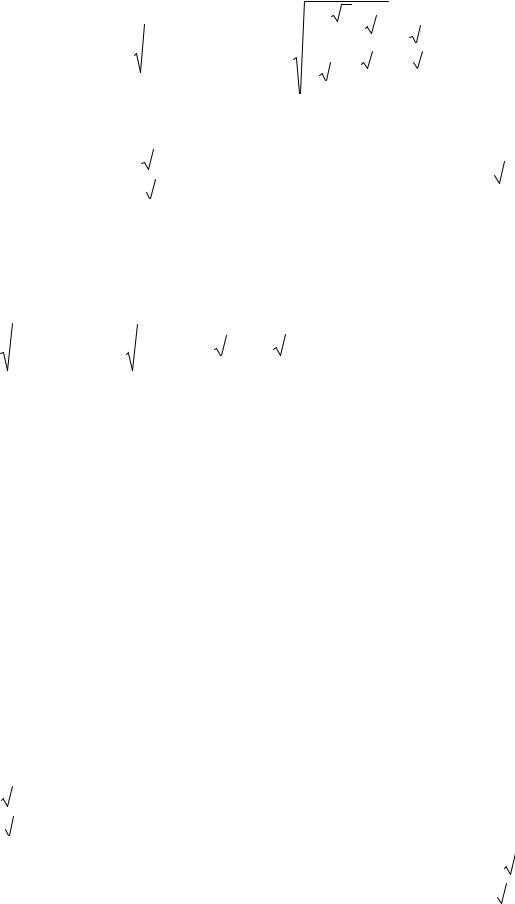
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S × |
3 |
× |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
S × sin 60 × tg 60 |
|
|
|
|
|
|
|
|
|
S . |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
h0 |
= |
|
|
|
|
= |
2 |
= |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 tg 60 - sin 60 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
- |
|
3 |
|
|
|
4 3 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
В рассматриваемой области D функция P(h,α ) |
имеет единственную |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
48S |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
критическую точку |
4 |
; |
3 |
, значение функции в ней равно P= |
|
|
. |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Исследуем функцию P(h,α ) |
на границе области D : |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
1) |
α = π , |
h > 0 . |
Имеем |
P(h,α ) = 2h + |
S |
|
|
|
Ph′ = 2 − |
S |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
h |
|
h2 |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
; π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
h = |
. Тогда P |
|
|
= 2 2S > |
4 48S 2 |
= P(h ;α |
|
) . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
2) |
При приближении точки |
|
(h,α ) |
|
к прямым |
h = 0 и α = 0 , а |
|||||||||||||||||||||||||||||||||||||||||||
также при удалении в бесконечность по h функция P(h,α )
неограниченно возрастает. Поэтому точку (h0 ,α 0 ) можно окружить таким
прямоугольником D1 = {(h,α ) / |
а ≤ α ≤ π , с ≤ h ≤ d} , что вне его и на |
|||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
его границе P(h;α ) > P(h0 ,α 0 ). |
|
|
|
|
|
|
|
|||||||
|
|
|
Отсюда следует, |
что P(h0 ,α 0 ) – наименьшее значение функции |
||||||||||
P(h,α ) в области D1 , и оно |
же |
будет наименьшим значением |
|
этой |
||||||||||
функции в области D . |
|
|
|
|
|
|
|
|
||||||
|
|
|
Итак, |
функция |
P(h,α ) |
имеет наименьшее значение при |
α =π, |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h = |
|
S |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||||
4 |
3 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
2 |
|
|
|
|
|||
|
|
|
Таким |
образом |
в трапеции |
ABCD : AB = BC = CD = |
|
S |
|
и |
||||
|
|
|
|
|
|
|
||||||||
|
|
|
27 |
|||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|||
ÐАВС = 120 .
34
§ 3. ПЕРВООБРАЗНАЯ И НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. ОСНОВНЫЕ ПРИЕМЫ ИНТЕГРИРОВАНИЯ
1. Основные понятия
Одной из основных задач дифференциального исчисления является нахождение производной функции или дифференциала заданной функции.
Основной задачей интегрального исчисления является обратная
задача – |
отыскание функции по ее |
производной |
или заданному |
ее |
|
дифференциалу. |
|
|
|
|
|
Функция F (x) называется первообразной для функции f (x), если |
|||||
функции F (x) и |
f (x) связаны следующим соотношением: |
|
|||
|
|
′ |
|
|
|
|
|
F (x) = f (x). |
|
|
|
Пример. |
Функция F (x) = sin x |
вяляется |
первообразной |
для |
|
функции |
f (x) = cos x , так как (sin x)′ = cos x . |
|
|
||
Если для данной функции f (x) существует первообразная, то она не является единственной. Так, в предыдущем примере в качестве первообразных можно взять следующие функции:
F (x) = sin x + 1, F (x) = sin x − 2
или в общем виде
F (x) = sin x + C ,
где C – произвольная постоянная, так как при любом значении C
(sin x + C )′ = (sin x)′ + (C )′ = cos+ 0 = cos x .
В связи с этим возникает вопрос, исчерпывает ли функция вида sin x + C все возможные первообразные для cos x или существуют еще функции другого вида, которые также будут первообразными для
Ответ на него дает следующая теорема.
Теорема. Если есть какая-либо из первообразных для данной функции f (x), то самое общее выражение для первообразной имеет вид:
35
F (x) + C ,
где C – есть первообразная постоянная.
Доказательство. Пусть F1 (x) есть любая функция, имеющая своей
производной F1′(x) = f (x).
С другой стороны, рассматриваемая функция F (x) также имеет
f (x) своей производной, то есть F ′(x) = f (x).
Вычитая это равенство из предыдущего, имеем:
F1′(x) − F ′(x) = (F1 (x) − F (x))′ = f (x)− f (x) ≡ 0
и, следовательно,
F1 (x)− F (x) ≡ C ,
где C есть постоянная, что и требовалось доказать.
Действительно, если производная некоторой дифференцируемой функции ϕ′(x) ≡ 0 , то сама функция ϕ(x) может быть только постоянной.
Полученный результат можно сформулировать и так: если производная (или дифференциалы) двух функций тождественно равны, то сами функции отличаются лишь постоянным слагаемым.
Если функция F (x) является первообразной для f (x), то семейство всех ее первообразных функций F (x) + C называется неопределенным
интегралом от функции |
f (x) и обозначается как ∫ f (x)dx . |
|
|
Таким образом, по определению |
|
||
|
|
∫ f (x)dx = F (x) + C , |
|
если |
|
|
|
|
|
′ |
|
|
|
F (x) = f (x). |
|
При |
этом функцию f (x) называют подынтегральной функцией, |
||
f (x)dx – |
подынтегральным выражением, переменную x – |
переменной |
|
интегрирования, а знак |
∫ – знаком интеграла. Действие, |
с помощью |
|
36
которого |
по |
данной |
функции f (x) находим |
ее |
первообразную F (x), |
||||||||
называется интегрированием функции |
f (x). |
|
|
|
|
|
|
||||||
|
|
Пример. Найти неопределенный интеграл от функции |
f (x) = x . |
||||||||||
|
|
Решение. Первообразной от x |
будет функция |
F (x) = |
x2 |
, так как |
|||||||
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
x2 |
′ |
|
|
|
x2 |
|
|
|
|
|
|
||
|
|
= x . |
В |
таком |
случае ∫ x dx = |
|
+ C , |
где |
C |
– |
произвольная |
||
|
|
||||||||||||
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
постоянная.
2. Таблица основных интегралов
Интегралы в приводимой ниже таблице называются табличными. В интегральном исчислении нет универсальных правил отыскания первообразных от элементарных функций. Методы нахождения первообразных сводятся к указанию приемов, приводящих данный (искомый) интеграл к табличному. Следовательно, необходимо знать табличные интегралы и уметь их узнавать.
Степенные функции:
∫ xn dx = |
xn+1 |
|
+ C (n ¹ -1); |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
n +1 |
|
|
|
|
|
|
|
|
|
|
||||
∫ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
|
dx = ln |
x |
|
+ C , т.к. |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
¢ |
|
|
1 |
, x > 0 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
¢ |
|
|
|
(ln x + C ) , x > 0 |
|
|
|
x |
|
|
|
1 |
|||||
(ln |
x |
+ C ) = |
|
¢ |
= 1 |
|
|
1 |
|
= |
x |
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(ln(- x)+ C ) , x < 0 |
|
- x |
× (-1) = |
|
, x > 0 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
||
Показательные функции:
∫ ex dx = ex + C ;
∫ a x dx = |
a x |
+ C (a > 0, a ¹ 1). |
|
ln a |
|||
|
|
37

Тригонометрические функции:
∫sin x dx = − cos x + C ;
∫cos x dx = sin x + C ;
∫tgx dx = − ln cos x + C ;
∫ctgx dx = − ln sin x + C ;
∫ 1 dx = tgx + C ; cos2 x
∫ 1 dx = −ctgx + C . sin 2 x
Дробные рациональные функции:
∫ |
1 |
dx = arctgx + C ; |
|
|
||||||||||
1 + x2 |
|
|
||||||||||||
|
1 |
|
|
= |
1 |
arctg |
x |
+ C (a > 0); |
||||||
∫ a2 + x2 dx |
|
|
|
|||||||||||
|
a |
|
|
|
a |
|
|
|||||||
|
1 |
|
|
1 |
|
|
x − a |
|
|
|||||
|
|
|
|
|
|
|
||||||||
∫ |
|
dx = |
|
ln |
|
|
|
+ C . |
||||||
x2 − a2 |
2a |
x + a |
||||||||||||
Иррациональные функции:
∫ |
|
|
1 |
|
dx = arcsin x + C ; |
||||||||||||
|
|
|
|
||||||||||||||
|
|
||||||||||||||||
1 |
− x2 |
|
|
|
|
|
|
|
|
|
|||||||
∫ |
|
|
1 |
|
|
|
|
|
|
dx = arcsin |
|
x |
+ C ; |
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
a2 − x2 |
|
||||||||||||||||
|
|
|
|
|
|
a |
|||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
dx = ln |
x + x2 + λ |
+ C . |
||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|||||||||||
x2 + λ |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
3.Основные свойства неопределенного интеграла
1.Если f (x) ≡ g(x), то ∫ f (x)dx = ∫ g(x)dx + C ,
где C – |
произвольная постоянная. |
|
2. |
(∫ f (x)dx)′ = f (x). |
(1) |
38

3.∫ F′(x)dx = F (x)+ C , где C – произвольная постоянная.
4. ∫ a f (x)dx = a∫ f (x)dx , a Î R , a ¹ 0 .
5.∫ ( f (x)± g(x))dx = ∫ f (x)dx ± ∫ g(x)dx .
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример. Найти ∫ 3x - |
|
+ |
|
|
x dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
∫ |
3x - |
+ |
|
|
= ∫ 3xdx - ∫ |
dx + ∫ |
|
xdx = |
|||||||||||||||||||||||
|
|
|
|
x dx |
|
|
|||||||||||||||||||||||||
x |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
+1 |
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
x 2 |
|
|
||||||||||
= 3∫ x1dx - 2∫ |
dx + ∫ x |
|
dx =3 × |
|
|
- 2 ln |
|
x |
|
+ |
|
|
+ C = |
||||||||||||||||||
2 |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
x |
|
|
|
|
1 +1 |
|
|
|
|
|
|
|
+1 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= 3 x2 - 2 ln x + 2 x
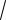 x + C.
x + C.
2 |
3 |
4. Простейшие способы интегрирования. Непосредственное интегрирование
Под непосредственным интегрированием понимают такой способ интегрирования, при котором данный интеграл удается привести к одному или нескольким табличным интегралам. К табличному виду обычно удается привести не очень сложные интегралы путем элементарных тождественных преобразований подынтегральных функций, а также воспользовавшись основными свойствами неопределенного интеграла. Поясним сказанное примерами.
Пример. Найти ∫ (x - 3)2 dx .
Решение.
∫(x - 3)2 dx = ∫ (x2 - 6x + 9)dx = ∫ x2 dx - ∫ 6xdx + ∫ 9dx =
=x3 - 6∫ xdx + 9∫ dx = x3 - 6 x2 + 9x + C = x3 - 3x2 + 9x + C. 3 3 2 3
39
