
4663
.pdfМинистерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
«Нижегородский государственный архитектурно-строительный университет»
М.И.Лиогонький
Элементы теории множеств и математической логики
Учебно-методическое пособие по подготовке к лекционным и практическим занятиям по дисциплине «Теория множеств и теория графов» для обучающихся по направлению подготовки 54.03.01 Дизайн,
профиль Промышленный дизайн
Нижний Новгород
2016
2
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
«Нижегородский государственный архитектурно-строительный университет»
М.И.Лиогонький
Элементы теории множеств и математической логики
Учебно-методическое пособие по подготовке к лекционным и практическим занятиям по дисциплине «Теория множеств и теория графов» для обучающихся по направлению подготовки 54.03.01 Дизайн,
профиль Промышленный дизайн
Нижний Новгород ННГАСУ
2016
3
УДК 519
Лиогонький М.И./ Элементы теории множеств и математической логики [Электронный ресурс]: учеб.-метод. пос. / М.И.Лиогонький; Нижегор. гос. архитектур. - строит. ун - т – Н. Новгород: ННГАСУ, 2016. – 56 с.– 1 электрон. опт. диск (CD-RW)
Излагаются основные понятия теории множеств и математической логики, приводятся многочисленные примеры их использования в других разделах курса «Теория множеств и теория графов»,приводятся задания для контрольной работы по разделу элементы теории множеств и математической логики.
Предназначено для обучающихся в ННГАСУ по дисциплине, «Теория множеств и теория графов» для обучающихся по направлению подготовки 54.03.01 Дизайн, профиль Промышленный дизайн
©М.И.Лиогонький 2016
©ННГАСУ, 2016
|
|
4 |
|
Содержание |
|
Элементы теории множеств и математической логики........................................................................................... |
1 |
|
1. Элементы теории множеств................................................................................................................................... |
5 |
|
1.1 |
Общие представления о множествах .............................................................................................................. |
5 |
1.2 |
Способы задания множеств. ............................................................................................................................ |
6 |
1.3 |
Подмножества. Универсальное множество. Множество всех подмножеств данного множества............. |
8 |
1.4. Конечные множества и их подмножества. О числе m-элементных подмножеств k-элементного множества. |
||
.................................................................................................................................................................................... |
|
10 |
1.4.1.Булеан множества. ....................................................................................................................................... |
10 |
|
1.4.2 Некоторые комбинаторные понятия и соотношения................................................................................ |
10 |
|
1.4.3 Мощность булеана конечного множества. ................................................................................................ |
12 |
|
1.5 |
Алгебраические операции над множествами. ............................................................................................ |
13 |
1.5.1. Определение основных операций.............................................................................................................. |
13 |
|
1.5.2 Поэлементное доказательство теоретико-множественных равенств. .................................................... |
14 |
|
1.5.3 Законы алгебры множеств........................................................................................................................... |
14 |
|
1.6 |
Счетные множества. ...................................................................................................................................... |
15 |
1.6.1 Определение счетного множества. ............................................................................................................. |
15 |
|
1.6.2 Свойства счетных множеств. ...................................................................................................................... |
15 |
|
1.7 |
Множества мощности континуум. ............................................................................................................... |
16 |
1.8 |
Прямое произведение множеств................................................................................................................... |
19 |
1.9 |
Бинарные отношения. Свойства бинарных отношений. ............................................................................. |
20 |
1.10 Отношение эквивалентности. Классы эквивалентности. ......................................................................... |
21 |
|
1.11 Отношение порядка ...................................................................................................................................... |
22 |
|
2 Элементы математической логики....................................................................................................................... |
23 |
|
2.1 |
Введение. ......................................................................................................................................................... |
23 |
2.1 |
Алгебра высказываний................................................................................................................................... |
25 |
2.1.1 Высказывания. Операции над высказываниями ....................................................................................... |
25 |
|
2.1.2 Правильно построенные формулы алгебры высказываний..................................................................... |
27 |
|
2.1.3 Тождественно истинные и тождественно ложные формулы. .................................................................. |
31 |
|
2.1.4 ДНФ,КНФ,СДНФ,СКНФ. ........................................................................................................................... |
32 |
|
2.2 |
Формальные системы. .................................................................................................................................... |
36 |
2.2.1 Определение формальной системы. ........................................................................................................... |
36 |
|
2.2.2 Исчисление высказываний.......................................................................................................................... |
37 |
|
. 2.3 Логика предикатов. ........................................................................................................................................ |
40 |
|
2.3.1 Понятие предиката....................................................................................................................................... |
40 |
|
2.3.2 Операции алгебры высказываний над предикатами................................................................................ |
43 |
|
2.3.3 Кванторы общности и существования. ...................................................................................................... |
46 |
|
2.3.4 Интерпретация формулы логики предикатов. Равносильные формулы................................................. |
48 |
|
2.3.5 Определение математических понятий посредством формул логики предикатов. ............................... |
50 |
|
Задания для контрольной работы по разделу элементы теории множеств и математической логики. ............ |
52 |
|
Литература............................................................................................................................................................. |
56 |
|
5
1.Элементы теории множеств
1.1Общие представления о множествах
Обычно, когда вводится какое-либо новое понятие, то оно опирается на из-
вестное понятие или известные понятия, частным случаем которого или кото-
рых оно является. Например, параллелограмм есть четырехугольник, у которо-
го противоположные стороны равны и параллельны. Окружность есть линия
на плоскости, все точки которой удалены от некоторой фиксированной точки
на некоторое фиксированное расстояние и т.д.
Понятие множества не имеет формального определенияоно первично. Один из создателей теории множеств Георг Кантор(1845-1918) сказал: «Множество есть многое, мыслимое нами как единое». Интуитивно, под множеством пони-
мается совокупность различных объектов, объединенных по какому-то одному или нескольким признакам.
Нет никаких ограничений на природу объектов, составляющих множество.
Так про окружность можно сказать, что это множество точек равноудаленных от фиксированной точки на расстоянии радиуса. Можно говорить о множестве сту-
дентов в данной аудитории, о множестве книг некоторой библиотеки, о множе-
стве букв некоторого алфавита, о множестве автомобилей на дорогах города, о
множестве целых числа от 1 до 1000, о множестве атомов серебра в данной мо-
нете или о множестве всевозможных идей, которые имело человечество, и т.д.
Множества часто обозначают прописными латинскими буквами A, B, C, X,Y.
Объекты, составляющие множество, называются элементами множества. Эле-
менты множеств обычно обозначаются строчными латинскими буквами x, y, a, b, c. Тот факт, что объект x принадлежит множеству A, передается записью x A
(читается – « элемент x принадлежит множеству A»). Если x не является элемен-
том A, то пишут x A.
Два множества А и В считаются равными (записывается А=В), если они состоят из одного и того же набора элементов. Т.е. А=В тогда и только тогда,
когда из того, что x A следует, что x В, а из того, что x В следует, что x A.
6
1.2 Способы задания множеств.
Существует два основных способа задания множеств: перечисление и опи-
сание. При первом способе просто перечисляются все элементы задаваемого множества. Например, множество букв алфавита некоторого языка определяется списком всех его букв, множество студентов в группе определяется студентами,
фамилия и имена которых совпадают со списком в журнале посещаемости, мно-
жество простых чисел меньших тысячи может быть задано перечислением всех таких чисел и т.д. В дальнейшем будем пользоваться общепринятыми обозначе-
ниями множеств:
N - множество натуральных чисел,
Z - множество целых чисел,
Q - множество рациональных чисел,
C - множество комплексных чисел,
R - множество действительных чисел.
Конечно, нельзя ни одно из этих множеств (хотя бы в силу их бесконечно-
сти), задать перечислением их элементов. Но опыт работы с элементами этих множеств позволяет предполагать, что в каждой конкретной задаче понятно, об
элементах каких из перечисленных множеств идет речь.
При втором способе элементы множества задаются при помощи характери-
стического свойства, устанавливающего какие элементы (принадлежащие, как
правило, некоторому объемлющему множеству) принадлежат задаваемому
множеству. В этом случае в фигурных скобках записывается произвольный эле-
мент множества и за вертикальной чертой записываются свойства, которыми этот элемент должен обладать:
A={x| P(x)} - A есть множество таких элементов x, которые обладают свой-
ствами P(x).
Свойства P(x) могут быть заданы или в виде словесного описания, или в ви-
де неравенств, или в виде уравнений.
Например, множество натуральных чисел от 1 до 1000 может быть записано таким образом N1000 = {x| x N и x≤ 1000}.
7
Множество, записанное следующим образом:
Ф={n| n N и уравнение xn+yn = zn имеет решение в целых числах}
связано с великой теоремой Ферма.
Однако состав множества, определенного описанием, не всегда очевиден, и
причина этого кроется гораздо глубже, чем просто недостаточная выразитель-
ность языка. Так только недавно было доказано (доказана теорема), что приве-
денное выше множество Ф состоит всего из двух элементов : Ф={1,2}.
Если множество содержит конечное число элементов, то говорят, что оно
конечно, в противном случае множество называется бесконечным.
Приведенные множества N1000 и Ф конечные, а описанные множества пар чисел
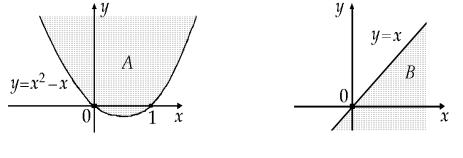
А={(x,y) y³ x2-x} и В={(x,y) y£ x},
геометрические интерпретации которых приведены на рис.1, являются беско-
нечными.
Рис.1 Само слово «множество» наводит на мысль, что в множестве содержится
много элементов. Но это не так. Можно рассматривать множества, состоящие всего из одного элемента, и даже множество, не имеющее ни одного элемента.
Последнее множество называется пустым множеством и для него существует обозначение: .
Например, множество
А= {x| х N и для любого натурального числа у N верно, что xу=у}
состоит всего из одного элемента, которым является 1, а множество
В={x| х N и x2+1=0}
8
не содержит элементов и, следовательно, В=Æ.
Все пустые множества равны между собой , иначе говоря, существует только
одно пустое множество.
1.3 Подмножества. Универсальное множество. Множество всех подмно-
жеств данного множества.
Понятие подмножества возникает тогда, когда необходимо рассматривать некоторое множество не самостоятельно, а как часть другого, более широкого множества.
Множество B называется подмножеством множества A (записывается
B A), если всякий элемент множества B является элементом множества A. За-
пись B A не исключает, что B=A. Пустое множество по определению является подмножеством любого множества.
По определению пустое множество является конечным. Также по определе-
нию множество является подмножеством самого себя, A A.
Таким образом, у каждого множества (кроме пустого) есть, по крайней мере,
два подмножества - само множество и пустое множество.
Истинным, строгим или собственным подмножеством множества А называется такое его подмножество В, что В А и В¹А (записывается ВÌА), где
Ì - знак строгого включения. По отношению к множеству А пустое множество и само множество А называются несобственными подмножествами множества А.
Рассмотрим следующие три множества A = { 0, 1 }, B = {{ 0, 1 },2} и
C = {{{ 0, 1 }, 2} 3}. Между ними справедливы следующие соотношения:
A B (т.к. само множество А является элементом множества В), B C (т.к.
само множество В является элементом множества С), но AÏС (т.к. само множество А не является элементом множества С). При этом множество А не является подмножеством множества В (т.к. 0 А, но 0Ï В) и множество В не яв-
ляется подмножеством множества С (т.к. 2 В, но 2ÏВ).
Очевидны следующие свойства множеств:
1. АÌВ «А В и А¹В.
9
2.А В « АÌВ или А=В.
3.АÌВ ® А В.
4.АÌВ® А¹В.
5.А В и В С ® А С.
6.АÌВ и ВÌС® АÌС.
7.АÍВ и ВÌС ® А С.
Покажем, например, выполнение свойства 5.
Докажем это методом от противного. Пусть А В и В С но А С и А¹С. Тогда существует такой элемент, что аÎА, но а С. Тогда, т.к. В С, то
аÏВ. Получили противоречие: аÎА, аÏВ, но А В.
Покажем выполнение свойства 6.
Так как АÌВ и ВÌС, то по свойству 3) АÍВ и ВÍС и по свойству 5) АÍС.
Осталось показать, что А¹С. Пусть это не так и А=С. То есть для любого элемен-
та а, из того, что а А следует, что аÎС. Так как ВÌС, то В¹ С и найдется эле-
мент b такой, что bÏВ, но bÎС. Так как АÌВ, то bÏА. Таким образом, элемент b
присутствует в множестве С, но отсутствует в множестве А, отсюда эти множе-
ства не равны.
Покажем выполнение свойства 7.
Так как ВÌС, то по свойству 3) ВÍС и тогда по свойству) АÍС. Осталось показать, что А¹С. Действительно, так как ВÌС, то найдется элемент а, аÎС, но
аÏВ. Так как АÍВ, то аÏА. Отсюда аÎС, но аÏА, т.е. А¹С.
Если все рассматриваемые в ходе рассуждений множества являются под-
множествами некоторого фиксированного множество J, то это множество назы-
вают универсальным множеством или универсом (для рассматриваемого набора множеств). Таким образом, универс (для рассматриваемого набора мно-
жеств) - это такое множество, что любое рассматриваемое множество является его подмножеством.
10
1.4. Конечные множества и их подмножества. О числе m-элементных
подмножеств k-элементного множества.
1.4.1.Булеан множества.
Если множество А конечное, то число его элементов будем называть его мощностью и обозначать это число с помощью записи А .
Рассмотрим множество А={a,b,c}. Для этого множества А =3. Найдем
все его различные подмножества. Таковыми будут: пустое множество Ø, три од-
ноэлементных подмножества {a}, {b}, {c}, три двухэлементных подмножества
{a,b}, {a,c}, {b,c} и одно трёхэлементное множество {a,b,c} (само множество А).
Т.е. существует всего 8 подмножеств этого множества.
Для произвольного множества А множество всех его подмножеств будем обозначать как S(A) или 2А. Множество S(A) или 2А называется булеаном мно-
жества А.
Наша ближайшая задача состоит в нахождении числа всех подмножеств ко-
нечного множества А (т.е. в определении мощности булеана множества А) и
числа подмножеств множества А, состоящих из m элементов.
1.4.2 Некоторые комбинаторные понятия и соотношения.
Пусть имеется множество А, состоящее из k различных элементов
А={a1,a2,…,a k}.
Перестановкой элементов этого множества назовем произвольное упорядо-
чивание его элементов. Сколько существует различных перестановок элементов множества А?
Обозначим это число P(k). Для ответа на вопрос рассмотрим такие переста-
новки, у которых на первом месте стоит элемент ai .(i=1,…, k). Очевидно, таких будет столько, сколько существует перестановок множества
А1={a1,a2,..,ak}/{ ai}, состоящего из (k-1) элементов т.е. P(k-1). Т.к. на
первом месте может стоять любой элемент из множества А, то получается со-
отношение P(k)=k*P(k-1), которое может быть продолжено так
P(k)=k* P(k-1)= k*(k-1)*P(k-2)=k*(k-1)*(k-2)*P(k-3)=….= =k*(k-1)*(k-2)*(k-3)*…*2* P(1).
