
3641
.pdfМинистерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
«Нижегородский государственный архитектурно-строительный университет»
Л.В. Филатов
ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
Учебно-методическое пособие по подготовке к практическим занятиям и выполнению расчетных работ
по дисциплине «Теория вероятностей и математическая статистика» для обучающихся по направлению подготовки 09.03.03 Прикладная информатика,
профиль Прикладная информатика в юриспруденции
Нижний Новгород
2018
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
«Нижегородский государственный архитектурно-строительный университет»
Л.В. Филатов
ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
Учебно-методическое пособие по подготовке к практическим занятиям и выполнению расчетных работ
по дисциплине «Теория вероятностей и математическая статистика» для обучающихся по направлению подготовки 09.03.03 Прикладная информатика,
профиль Прикладная информатика в юриспруденции
Нижний Новгород ННГАСУ
2018
1
УДК 519.2
Филатов Л.В. / Проверка статистических гипотез [Электронный ресурс]: учеб.-метод. пос. / Филатов Л.В; Нижегор. гос. архитектур. - строит. ун - т – Н. Новгород: ННГАСУ, 2018.
– 40 с. – 1 электрон. опт. диск (CD-RW)
В пособии рассматривается основные положения теории проверки статистических гипотез. Описываются алгоритмы построения критериев проверки гипотез о виде распределения случайных величин, о значении неизвестных параметров распределения, о значимости свойств выборочных совокупностей. Даются основные понятия и формулы, примеры решения задач, набор расчетных заданий и контрольных вопросов для самопроверки материала.
Пособие предназначено для обучающихся в ННГАСУ по дисциплине «Теория вероятностей и математическая статистика» для обучающихся по направлению подготовки 09.03.03_Прикладная информатика, профиль Прикладная информатика в юриспруденции.
© |
Л.В. Филатов, 2018 |
© |
ННГАСУ, 2018 |
2
1. Введение
Имея дело со случайными величинами в различных областях человеческой деятельности, часто приходится высказывать предположения о виде распределения случайной величины или о значениях ее параметров. Эти предположения,
называемые статистическими гипотезами, строятся с целью прогнозирования поведения случайной величины и принятия решений в условиях неопределенности.
Высказанная статистическая гипотеза должна быть проверена по результатам наблюдений (измерений) случайной величины, в результате чего гипотеза принима-
ется или отвергается с определенной степенью риска совершить ошибку.
Задачи проверки статистических гипотез, связанные с формулировкой и ана-
лизом критериев такой проверки, составляют предмет обширного раздела совре-
менной математической статистики и рассматриваются в настоящем методическом пособии.
2. Простые и сложные статистические гипотезы.
Статистическая гипотеза Н называется простой, если она однозначно опреде-
ляет закон распределения случайной величины Х, например, для непрерывных ве-
личин в виде функции распределения Fх(x, θ) или функции плотности распределе-
ния вероятности fх(x, θ) c определенными значениями параметров θ. При этом, ве-
роятность попадания значений одномерной случайной величины Х в интервал
[х1,х2] может быть вычислена по формулам:
x |
|
d |
|
|
Р(х1<X< х2) = Fх(x2, θ) - Fх(x1, θ) = ∫2 |
f x (x,θ )dx ; fх(x, θ) = |
Fх(x, θ) |
||
|
||||
x1 |
|
dx |
||
|
|
|
||
Гипотеза является сложной, если в ней неизвестный закон распределения предполагается принадлежащим к некоторому допустимому множеству распределе-
ний.
3
Пример простой статистической гипотезы Н1:
Длина ж/б перекрытия распределена по нормальному закону N(a,σ) cо сле-
дующими параметрами: математическое ожидание а=600см, среднеквадратическое отклонение σ=0,75см.
Пример сложной статистической гипотезы Н2:
Толщина ж/б перекрытия распределена по нормальному закону N(a,σ) cо сле-
дующими параметрами: математическое ожидание а=20см, среднеквадратическое отклонение σ<0,75см.
Ясно, что сложная гипотеза состоит из множества простых гипотез. Это мно-
жество (конечное или бесконечное) может быть описано изменением некоторого параметра h в определенных пределах. Так, в приведенном примере Н2={
Н1(а=20, σ=h); 0<h<0,75}.
Статистическими гипотезами являются так же и некоторые макро утвержде-
ния, вытекающие из предположения о виде закона распределения случайной вели-
чины и имеющие определенное практическое значение. Так, например, утверждение
Н3 о том, что поступившая на предприятие большая партия продукции содержит недопустимый процент брака, основано на предполагаемом законе распределения количества брака в данной партии.
3. Проверка статистических гипотез.
Выдвинутая статистическая гипотеза Н должна быть проверена. Как и в лю-
бой другой науке, критерием ее проверки является опыт, т.е. наблюдение (измере-
ние) случайной величины. В математической статистике эти наблюдения представ-
ляются выборкой ХВ={xi, n} ={x1, x2, …… x n} объема n. Критерий проверки должен отвергать или принимать гипотезу по результатам наблюдения. В силу случайной природы наблюдаемых в выборке значений xi, в результате применения критерия возможны следующие четыре случайные события, их вероятности и совершаемые
при этом ошибки:
4
|
Таблица 1 |
|
|
|
|
|
|
|
|
|
Наличие |
Результат проверки гипотезы |
Вероятность |
|
|
|
|
|
ошибки |
|
|
|
|
Гипотеза Н отвергается, когда она верна |
α |
|
ошибка I-рода |
|
|
|
|
Гипотеза Н принимается, когда она верна |
1 − α |
|
нет ошибки |
|
|
|
|
Гипотеза Н принимается, когда она не верна |
β |
|
ошибка II- |
|
|
|
рода |
|
|
|
|
Гипотеза Н отвергается, когда она не верна |
1 − β |
|
нет ошибки |
|
|
|
|
Из таблицы видно, что с вероятностью α при проверке может быть совершена ошибка I-рода, когда отвергается верная гипотеза и с вероятностью β ошибка II-
рода, когда принимается не верная гипотеза. Поэтому первым требованием к крите-
рию проверки является минимизация вероятности ошибок, однако здесь нужно от-
метить два существенных момента:
Во-первых, ошибки I и II рода могут иметь различную значимость с точки зрения их последствий. Так, например, для гипотезы Н ={Партия ж/б перекрытий аварийно опасна и не должна поставляться на стройки} ошибка I.рода приводит к поставке на стройку аварийно опасных изделий, что может повлечь человеческие жертвы. Ошибка же II рода здесь приводит к забраковыванию безопасной партии изделий, что влечет к экономическим потерям завода ЖБК. Ясно, что значимость ошибки I рода в приведенном примере выше, чем ошибки II рода, т.к. человеческие жертвы не сравнимы с любыми потерями и не допустимы. Принято считать, что ошибки I рода более значимы чем ошибки II рода, если это не так, то проверяемую гипотезу необходимо переформулировать соответствующим образом (например,
перейти к противоположной гипотезе).
Во-вторых, ошибки I и II рода находятся в некотором противоречии друг с другом, поскольку, если при построении критерия уменьшать вероятность одной из
5
них, то вероятность другой будет возрастать. Так, например, при использовании гипотетического критерия, отвергающего любую гипотезу, ошибки II рода совер-
шаться не будут (β=0, “ ложь не пройдет”), но при этом всегда будем совершать ошибку I рода ( α=1, ” истина не установиться“).
Учитывая сказанное, при построении критерия проверки статистической ги-
потезы необходимо, сначала задаться допустимым уровнем риска совершить ошиб-
ку I рода, как наиболее значимую, а затем минимизировать ошибки II рода.
4. Построение критерия проверки гипотезы.
Пусть необходимо проверить простую гипотезу H0={X fх(x, θ)}, состоящую в предположении о виде функции плотности распределения случайной величины Х с
вполне определенными параметрами θ. Построим критерий, однозначно прини-
мающий или отвергающий проверяемую гипотезу по полученной в наблюдении за случайной величиной Х выборке ХВ={x1, x2, x3, …… x n} объема n. Помимо основной гипотезы H0 (“ нулевой”) рассмотрим еще одну или несколько альтернативных гипо-
тез H1,H2,H3, …,H m каждая из которых противоречит основной.
Критерий проверки гипотезы состоит из двух составляющих:
Во-первых в качестве критерия принимается некоторая случайная величина К,
с известными распределениями при условии справедливости основной и альтерна-
тивных гипотез fK(k Hj) j=0,1, ..m и значения которой можно вычислить по наблюдаемой выборке ХВ, т.е. kнабл= ϕ(хi).
Во-вторых, строится решающее правило для критерия проверки, согласно ко-
торого гипотеза будет приниматься или отвергаться. Для этого, назовем критиче-
ской областью критерия те значения величины К, при которых гипотеза отвергает-
ся. Критическую область будем обозначать Ккр. Тогда решающее правило критерия
проверки будет следующим:
kнабл |
Ккр |
H0 отвергается (по наблюдаемой выборке), |
kнабл |
Ккр |
H0 принимается (нет оснований отвергать гипотезу) |
6
Точки значения критерия К, где критическая область критерия проверки Ккр отделя-
ется от области принятия гипотезы Кпр, называются критическими точками крите-
рия kкр. Как построить критическую область критерия, или что равносильно, как найти критические точки критерия? Ниже рассмотрим ответ на этот вопрос.
Зададимся вероятностью ошибки I рода, как наиболее значимой. Исключить такую ошибку при проверке гипотезы невозможно (a¹0), но в вероятностных зада-
чах это не является трагедией. На практике обычно эту вероятность задают достаточно малой величиной a=0,05; 0,0025; 0,005 и называют уровнем значимости кри-
терия. Если из условия
Р( kÎ Ккр ) = ∫ fK( k H0 ) dx = a,
Kкр
можно определить критические точки kкр однозначно, то задача построения крити-
ческой области критерия решена. В противном случае, когда еще остается свобода выбора критических точек, рассмотрим влияние альтернативных гипотез. Посколь-
ку величина
∫ fK( k Hj ) dx = 1 - bj, j=1,..m
Kкр
есть вероятность правильного отбрасывания H0 при условии справедливости Hj, то ее называют мощностью критерия по отношению к альтернативной гипотезе Hj. По-
этому, при заданном уровне значимости a, критическую область критерия нужно строить так, чтобы мощность критерия была максимальной, а именно:
(1 - bj ) max , для наиболее мощного критерия (НМК) относительно гипо-
тезы Hj , максимизация проводится по параметрам сложной гипотезы Hj.
min (1 - bj ) max, для равномерно наиболее мощного критерия (РНМК), в
случае наличия нескольких сложных гипотез.
Величина bj есть вероятность принять неверную гипотезу H0 при условии справедливости альтернативной гипотезы Hj. На рисунке 1 приведена графическая интерпретация алгоритма построения критической области одномерного критерия.
7
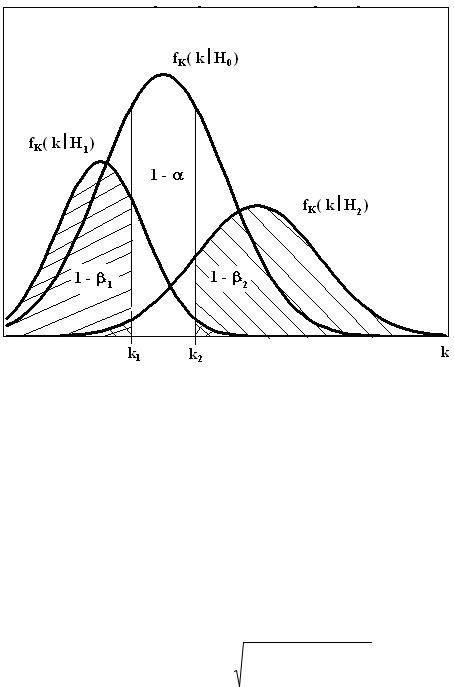
Видим, что структура критической области зависит от наличия альтернативных ги-
потез и их расположения относительно основной гипотезы.
Рис. 1. Двухсторонняя критическая область критерия Ккр={ k>k2, k<k1} при наличии двух альтернативных гипотез Н1, Н2.
5. Примеры построения критериев проверки гипотез о значении параметров
распределения нормальной случайной величины.
По данным выборки ХВ={хi, n} могут быть получены выборочное среднее Хср
и выборочный стандарт S:
|
1 |
n |
|
1 |
n |
|
Хср= |
∑ x j , |
S = |
∑( X ср − x j )2 . |
|||
n |
|
|||||
|
j =1 |
|
n − 1 j =1 |
|||
Эти величины являются случайными и по ним могут быть построены оценки мате-
матического ожидания а=М[X] и дисперсии σ2=D[X] наблюдаемой в выборке слу-
чайной величины Х. Так, точечные оценки:
а* =Хср; (σ2) = S2
8

являются несмещенными, состоятельными оценками характеристик наблюдаемой величины [1], однако об их точности и эффективности можно говорить лишь, ис-
следовав вероятностные свойства этих оценок.
Ясно, что точность оценки возрастает с увеличением объема выборки, но большие выборки часто неприемлемы на практике. Поэтому построение эффективных оце-
нок, обладающих требуемой точностью на малых выборках, является важнейшей задачей математической статистики.
Для проведения анализа вероятностных свойств оценок необходимо знать за-
кон распределения наблюдаемой величины Х, который в приложениях обычно не-
известен точно, но может быть предположен в виде гипотезы.
Пусть случайная величина Х распределена нормально по закону N(а, σ) с не-
известными параметрами а, σ и наблюдается в выборке XB={xi, n} объема n. Нор-
мальный закон распределения N(а, σ) задается следующей функцией плотности распределения вероятности:
|
1 |
|
|
(х − а) 2 |
||
fX(x)= |
|
|
|
exp(− |
|
) ; M[Х]=а, D[Х]= σ2. |
σ |
|
|
2σ2 |
|||
2π |
||||||
Ниже проверим ряд простых статистических гипотез об истинных значениях
параметров нормальной случайной величины Х.
5.1. Проверим гипотезу о том, что истинная (гипотетическая) дисперсия слу-
чайной величины равна σ02. Проверяемая гипотеза Н0={σ2=σ02}. В качестве критерия
возьмем одномерную случайную величину К, имеющую распределение «хи-
квадрат» с n-1 степенями свободы:
К=(n-1) S2/σ 2, |
f |
( k H |
0 |
) = χ2(k,n-1), M[K]=(n-1), D[K]= 2(n-1). |
0 |
K |
|
|
Задаваясь уровнем значимости α для проверяемой гипотезы Н0 будем строить критическую область Ккр в зависимости от вида единственной конкурирующей
(альтернативной) гипотезы H1 в следующих случаях:
Случай А: Н1={σ2>σ02}. В этом случае при справедливости конкурирующей гипотезы ожидаем сдвиг наиболее вероятных значений критерия К в большую сто-
рону, поэтому критическая область критерия будет правосторонней.
9
