
3480
.pdf
[Введите текст]
1.17. Эллипс проходит через точки M (
 3,−2) и N (− 2
3,−2) и N (− 2
 3,1). Составить уравнение эллипса, приняв его оси за оси координат.
3,1). Составить уравнение эллипса, приняв его оси за оси координат.
1.18. Составить уравнение гиперболы, проходящей через точку A(9,−8), если асимптоты ее заданы уравнениями 
 2x ± 3y = 0 .
2x ± 3y = 0 .
1.19.Написать каноническое уравнение параболы с вершиной в
начале координат, если известно, что ее фокус находится в точке пересечения прямой 4x − 3y − 4 = 0 с осью ox .
1.20.Написать уравнение окружности, центр которого находится в
правом фокусе гиперболы |
x2 |
|
− |
y 2 |
= 1, а радиус равен расстоянию между |
|
|
||||
25 |
16 |
|
|||
фокусами этой гиперболы. |
|
|
|
||
1.21. Струя воды, выбрасываемая фонтаном, принимает форму |
|||||
параболы, параметр которой |
p = 0,1. Определить высоту струи, если |
||||
известно, что она падает в бассейн на расстоянии 2 метра от места выхода.
1.22. Фокусы гиперболы совпадают с фокусами эллипса x2 + y 2 = 1. 16 25
Составить уравнение гиперболы, если ее эксцентриситет равен 1,5 .
1.23. Найти уравнение гиперболы, вершины которой находятся в
фокусах эллипса x2 + y 2 = 1, а фокусы гиперболы находятся в вершинах
16 25
данного эллипса.
1.24.Найти уравнение окружности, симметричной с окружностью
x2 + y 2 = 9 относительно прямой x − y = 6 .
1.25.Найти уравнение эллипса, вершины которого находятся в
фокусах гиперболы x2 − y 2 = 1, а фокусы в вершинах данной гиперболы.
1625
1.26.Определить угол между асимптотами гиперболы, если расстояние между фокусами вдвое больше расстояния между директрисами.
1.27.Мостовая арка имеет форму параболы. Определить параметр этой параболы, зная, что пролет арки равен 24м, а высота 6м.
1.28.Через точку M (2,−5) провести прямые, параллельные
асимптотам гиперболы x2 − 4 y 2 = 4 .
1.29.Камень, брошенный под острым углом к горизонту, описал дугу параболы и угол на расстоянии 16м от начального положения. Определить параметр параболической траектории, зная, что наибольшая высота, достигнутая камнем, равна 12м.
1.30.На гиперболе 16x 2 − 49 y 2 = 784 найти точку, которая была бы в
три раза ближе к одной из асимптот, чем к другой.
21
[Введите текст]
Задание 2
Установить тип кривой, заданной общим уравнением. С помощью преобразования координатных осей привести уравнения кривых к каноническому виду. Построить кривые в старой и новой системах координат.
2.01.
1.xy − 3x − 3y + 2 = 0 .
2.3x2 + 4 y − x + 2 = 0 .
3.x2 + y2 − 4x + 2 y −15 = 0 .
4.3x2 − 4 y2 + x − 6 = 0 .
5.2x2 + 6 y2 + x + 2 y − 16 = 0
2.02.
1.2xy + x − 2 y − 4 = 0 .
2.x2 + 2x + y2 − 4 = 0 .
3.2x2 − x + y + 4 = 0
4.3x2 + 4 y2 + 6x + 8 y −15 = 0 .
5.x2 − y2 + 2x + 3y + 4 = 0
2.03.
1.0,5xy + x − y − 3 = 0
2.2x2 + 2 y2 − 4x −10 = 0
3.3x2 − x + y − 3 = 0
4.4x2 − 3y2 + 8x + 6 y −10 = 0
5.x2 + 2 y2 + x − 4 y −12 = 0
2.04.
1.3x2 + 6x − y − 2 = 0
2.xy − 3y + x + 4 = 0
3.2x2 + 6 y2 +12 y = 0
4.x2 + y2 + 4x + 4 y = 0
5.3x2 − 2 y2 + 4 y + 4 = 0
2.05.
1.4 y2 − 8 y + 3x − 5 = 0
2.x2 − 3y 2 − 6 y + 2x +1 = 0
3.2xy − 3y + x +1 = 0
22
[Введите текст]
4.x2 + y2 − 2 y + 2x +1 = 0
5.2x2 + y 2 + 2 y + 4x +1 = 0
2.06.
1.2xy − 3y +1,5x − 2 = 0
2.y2 + y − 3x + 2 = 0
3.3x2 + y2 − 2 y = 0
4.3x2 − y2 − 2x − 2 y = 1
5.x 2 + y 2 + x + y = 1
2.07.
1.4x2 − y 2 − 2 y + x +1 = 0
2.2x2 + 4x − 3y +1 = 0
3.2xy − 3y − 2x + 3 = 0
4.x2 + y2 + 4x − 2 y + 2 = 0
5.2x2 + y 2 + 4 y +1 = 0
2.08.
1.2x2 + 2 y2 + 4x +1 = 0
2.x2 − y2 − 2 y + 2x = 0
3.3xy − 2 y − x +1 = 0
4.2x2 + 4 y2 + 2x + 3y = 0
5.3x2 − 6x + y − 4 = 0
2.09.
1.3x2 + 4 y 2 + 6x − 8y + 1 = 0
2.5x2 + 10x − 4 y = 0
3.x2 + y 2 − 2x + 4 y + 2 = 0
4.2xy − y − x + 3 = 0
5.3x2 − 4 y 2 + 6x + 4 y + 10 = 0
2.10.
1.6x2 + 2 y2 + 12x − 4 y + 1 = 0
2.xy − 4 y − 2x + 3 = 0
3.x2 + y 2 − 4x + 2 y + 2 = 0
4.− 2x2 + 3x − 2 y + 1 = 0
5.6x2 − 8 y2 + 12x + 16 y + 3 = 0
2.11.
1.x2 + y 2 − 2x + 4 y + 5 = 0
2.9xy − 20 y − 10x − 10 = 0
23
[Введите текст]
3.x2 − 2 y 2 − 4x + 4 y + 4 = 0
4.6 y 2 − y 2 + 2x − 4 = 0
5.x2 + 2 y 2 − 4x − 2 y + 1 = 0
2.12.
1.2xy − x + 2 y − 3 = 0
2.x2 − 3y 2 + 2x − 6 y + 2 = 0
3.5x2 − 2x − y + 4 = 0
4.x 2 + y 2 + 2 y − 2x = 0
5.2x2 + y2 + 4x − 2 y + 2 = 0
2.13.
1.x2 + y 2 + 4 y + 1 = 0
2.xy − 2 y + 3x − 3 = 0
3.2x2 + 3y2 − x + y + 1 = 0
4.3x2 + x − y + 5 = 0
5.x2 − 3y 2 + 2x − 6 y + 4 = 0
2.14.
1.2x2 − 3y 2 + 2x − 6 y + 4 = 0
2.x2 + y 2 + 6x − 8 y + 10 = 0
3.xy − 3y + 2x − 2 = 0
4.4 y 2 + 2 y + 3x = 0
5.2x2 + 3y 2 + 4x − 6 y + 3 = 0
2.15.
1.x2 − 5y 2 + 4x − 10 y + 4 = 0
2.7x2 − 14x + 2 y − 7 = 0
3.3x2 + y2 + 6x − 2 y + 1 = 0
4.xy − x − 2 y + 1 = 0
5.x2 + y 2 + 2x + 4 y + 2 = 0
2.16.
1.x2 + y 2 + 4x − 6 y = 0
2.2xy − 3x + 2 y − 4 = 0
3.7x2 − 3x + 4 y + 1 = 0
4.2x2 + y 2 + 6x + 3 = 0
5.3x2 − 4 y 2 + x − y + 4 = 0
2.17.
1. 3xy + x − y + 6 = 0
24
[Введите текст]
2.x2 + y 2 − 8x + 6 y + 2 = 0
3.6x2 − 3x + y + 1 = 0
4.2x2 − 5 y 2 + 10 y + 5 = 0
5.3x2 + 5y 2 + 6x − 10 y + 4 = 0
2.18.
1.x2 + y 2 + 4x − 6 y = 0
2.3x2 − y 2 + 6x + 2 = 0
3.2xy + 3y − x + 3 = 0
4.2x2 + 3x + y = 0
5.4x2 + 5 y2 + 8x − 10 y + 4 = 0
1.− x2 − 32x + y + 6 = 0
2.x2 + y 2 + 4x + 2 = 0
3.1,5xy + x − 0,5 y + 1 = 0
4.3x2 + y 2 − 6x + 2 y + 3 = 0
5.4x2 − 3y 2 + 16x + 6 y + 10 = 0
2.20.
1.2 y 2 + 5x + 4 y + 1 = 0
2.x2 + y 2 − 4x − 2 y + 2 = 0
3.5xy + x − y + 1 = 0
4.2x2 − y 2 + 4x − y + 4 = 0
5.2x2 + 3y 2 + 4x + 6 y + 4 = 0
2.21.
1.3y 2 − 6 y + 2x − 7 = 0
2.x2 + y 2 + 2x − 6 y + 4 = 0
3.4xy + x − 2 y − 3 = 0
4.2x2 + 3y2 + x − y − 1 = 0
5.2x2 − y 2 − 2x − y + 4 = 0
2.22.
1.x2 + y 2 + 6x − 4 y + 0,5 = 0
2.2 y2 + 3x + 6 y + 7 = 0
3.x2 − 3y2 + 2x − 6 y + 4 = 0
4.3x2 + y2 + 4x − 2 y + 3 = 0
5.− xy + 2 y − 3x + 1 = 0
25
[Введите текст]
2.23.
1.x2 + y2 + 2x − 2 y +1 = 0
2.3y2 + 3x + 2 y = 0
3.3x 2 − y 2 + 4x + y = 0
4.5xy + x − y + 3 = 0
5.3x2 + 6 y2 + 6x +12 y + 2 = 0
2.24.
1.− 2x2 + y +10 = 0
2.x2 + y2 + 4x + 6 y + 4 = 0
3.4xy + x − 3y +1 = 0
4.3x2 − 5 y2 + 6x +10 y + 5 = 0
5.3x2 + 4 y2 −12x +12 y +12 = 0
2.25.
1.0,5xy + x − 2 y − 2 = 0
2.2x2 + 2 y2 + 4x + y = 4
3.3x2 − 4x + y −1 = 0
4.2x2 − y2 + 2 y + 4 = 0
5.2x2 + 3y2 + 4x + 6 y + 5 = 0
2.26.
1.3x2 + 7x + 2 y + 6 = 0
2.4xy + 3x − y + 2 = 0
3.x2 + y2 + 6 y − 3x +1 = 0
4.3x2 + 7 y2 + 6x −14 y +10 = 0
5.4x2 − 5 y2 − 8x +10 y + 5 = 0
2.27.
1.x2 + y2 − 2x + 4 y + 4 = 0
2.3x2 − y2 + 2 y − 6x +1 = 0
3.5xy + 6x − 3y + 2 = 0
4.5x2 + 6 y2 −10x +12 y + 4 = 0
5.4 y2 + y − 3x + 2 = 0
2.28.
1.2x 2 − 4 y 2 + 4x − 8 y + 2 = 0
2.2xy + 6 y − 2x +1 = 0
3.x 2 + y 2 + x − 2 y = 0
4.3x2 + y2 + 6x − 4 y = 0
26
[Введите текст]
5. 3x2 + 6x − 4 y +1 = 0
2.29.
1. x2 + y2 + 6x − 2 y +1 = 0 2. 2x2 − y2 + 4x − 6 y + 4 = 0 3. 4xy + x − y +1 = 0
4. 2x2 + 3y2 + 4x + 6 y + 4 = 0 5. 2x2 + 2x + 5y +1 = 0
2.30.
1. 7x2 −14x + 2 y − 3 = 0
2. 3x2 − y2 + 6x − 2 y +1 = 0 3. x2 + 5y2 + 4x −10 y + 2 = 0 4. x2 + y2 − 6x + 4 y+ = 0
5. 2xy − x + 3y − 4 = 0
§ 7. Параметрическое задание кривых на плоскости.
Пусть заданы две функции одного аргумента
x = x (t ) |
(17) |
|
|
y = y (t ), |
|
где a ≤ t ≤ b (в частности допускается a = −∞ ; b = +∞ ). При каждом значении t числа x(t) и y(t) будем понимать как координаты некоторой точки на плоскости, причем эта точка, вообще говоря, меняется вместе с
изменением |
t , описывая некоторую кривую |
L . В этом случае систему |
||||||
уравнений |
(17) называют параметрическими |
уравнениями линии L , а |
||||||
аргумент t |
называют параметром. |
уравнений к уравнению F (x, y) = 0 |
||||||
Переход от параметрических |
||||||||
осуществляется исключением параметра t из системы уравнений (17). |
||||||||
Рассмотрим несколько примеров. |
|
|
|
|
|
|||
x = x0 + lt |
параметрические |
уравнения |
прямой, |
|||||
1. |
|
– известные |
||||||
y |
= y0 + mt |
|
|
|
|
|
{l, m}, |
|
|
через точку (x0 , y0 ) |
|
|
|
|
|||
проходящей |
с направляющим |
вектором |
a |
|||||
− ∞ < t < +∞ . |
|
|
|
|
|
|
||
x = t 2 |
|
|
|
|
|
|
||
2. |
|
. Исключая параметр t , получаем x = y 2 , то есть уравнение |
||||||
y |
= t |
|
|
|
|
|
|
|
параболы, − ∞ < t < +∞ .
27
[Введите текст]
3. |
x = R cos t |
– |
уравнения окружности радиуса R , т.к. |
|
Уравнения |
|
|||
|
y = R sin t |
|
|
|
x 2 + y 2 |
= R 2 cos2 t + R2 sin 2 t = R2 , |
0 ≤ t ≤ 2π . |
||
4. |
x = a cost |
, |
0 |
≤ t ≤ 2π – являются параметрическими |
Уравнения |
||||
|
y = b sin t |
|
|
|
уравнениями эллипса.
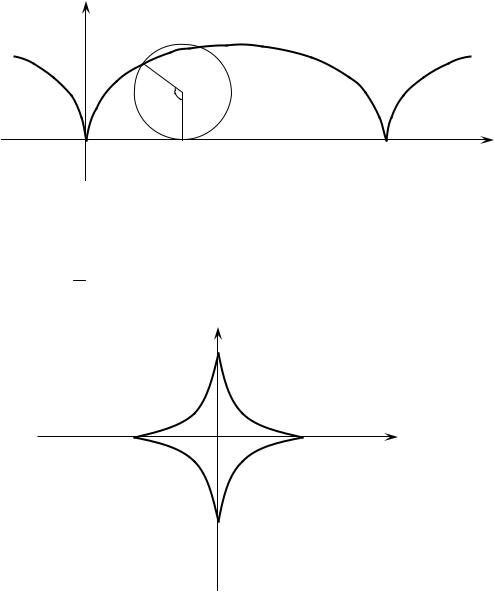
5. Циклоида.
Пусть по прямой без скольжения катится круг радиуса a . Кривая, описываемая фиксированной точкой круга, называется циклоидой.
x = a(t − sin t ) |
, 0 |
≤ t ≤ 2π . |
|
Уравнения циклоиды |
− cost ) |
||
y = a(1 |
|
|
|
y
2 a
O1
t
O |
2π a |
x |
Рис. 19.
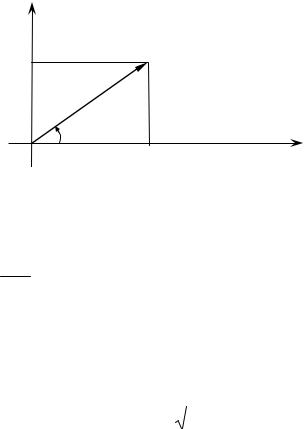
6. Астроида.
Пусть по окружности радиуса a внутри нее катится без скольжения
круг радиуса a . Траектория, которую описывает фиксированная точка, 4
лежащая на границе подвижного круга, называется астроидой. y
-а |
a |
x
Рис. 20.
28

[Введите текст]
x = a cos3 t
Уравнения астроиды , 0 ≤ t ≤ 2π .
y = a sin3 t
7. Кардиоида.
Пусть по окружности радиуса a вне ее катится без скольжения круг того же радиуса a . Кривая, которую описывает фиксированная точка подвижного круга, называется кардиоидой.
y
M (x, y)
O |
a |
x |
Рис. 21.
x = a(2cost − cos 2t )
Уравнения кардиоиды ( ) , 0 ≤ t ≤ 2π .
y = a 2sin t − sin 2t
§ 8. Кривые в полярной системе координат.
Рассмотрим полярную систему координат на плоскости. Пусть нам задан полюс и полярная ось. Для произвольной точки M на плоскости обозначим через ρ расстояние от точки O до точки M , а через ϕ – угол, на который нужно повернуть полярную ось до совмещения с лучом.
ρ
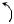 ϕ
ϕ
О
Рис. 22.
29
[Введите текст]
Числа ϕ , ρ называются полярными координатами точки M . Число
ρ называют полярным радиусом (всегда |
ρ ³ 0 ), |
а число |
ϕ называют |
полярным углом точки M . Полярный |
радиус |
для любой точки |
|
определяется однозначно, а полярный угол – с точностью до |
2π n , где n – |
||
целое число.
Пусть на плоскости задана полярная и правая декартова прямоугольная система координат.
y
y |
|
M |
|
|
|
|
|
|
ρ |
|
|
|
ϕ |
|
|
0 |
|
x |
x |
|
|
||
Рис. 23. |
|
|
|
Пусть |
M – |
произвольная точка плоскости, имеющая декартовы |
|
координаты |
(x, y) |
и полярные координаты (ϕ, ρ ). Рассмотрим радиус |
|
вектор OM точки M . Сравнивая координаты, получим формулы перехода от декартовых координат к полярным:
x = ρ cos ϕ , y = ρ sinϕ .
Формулы перехода от полярных координат (ϕ , ρ ) к декартовым (x, y) можно записать в виде:
ρ = |
|
|
, tgϕ = |
y |
(x ¹ 0). |
||
x2 + y 2 |
|||||||
|
|||||||
|
|
|
|
|
x |
||
При x = 0 можно вычислить |
ctgϕ = |
x |
. |
||||
|
|||||||
|
|
|
y |
||||
Кривую в полярных |
координатах задают в виде уравнения |
||||||
F (ϕ, ρ ) = 0 или явного уравнения в виде ρ = f (ϕ ).
Рассмотрим несколько примеров кривых, заданных в полярных координатах.
1.Уравнение ρ = a , где a – постоянное число, задает окружность радиуса a , центр которой совпадает с полюсом O .
2.Уравнение ϕ = t определяет луч, исходящий из полюса и составляющий угол t с полярной осью. t – произвольное число.
30
