
2939
.pdf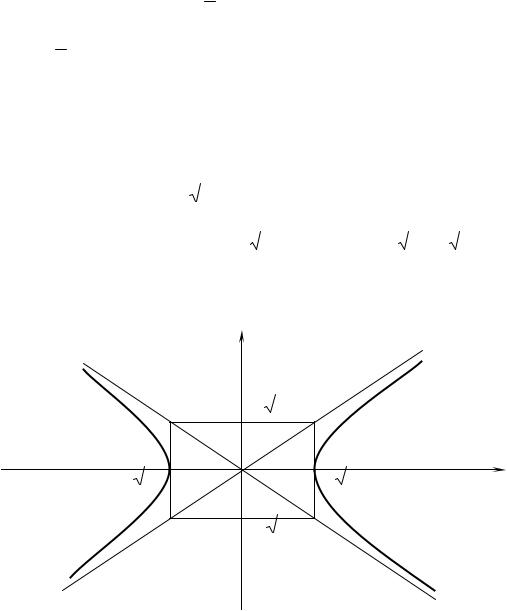
Пример. Точка M (6,-2
 2 ) лежит на гиперболе, уравнения асимптот которой y = ± 2 x . Составить уравнение гиперболы и построить ее.
2 ) лежит на гиперболе, уравнения асимптот которой y = ± 2 x . Составить уравнение гиперболы и построить ее.
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Каноническое уравнение гиперболы |
x2 |
|
- |
y 2 |
=1, т.к. асимптоты |
||||||||||||||||||||||||||||||||||||
|
|
a 2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b2 |
|
|
|
|
|
||||||
|
y = ± |
2 |
x , то |
b |
= |
2 |
, b = |
2 |
|
a . Подставим последнее в уравнение гиперболы: |
|||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
3 |
|
|
|
a |
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 × 9 |
|
|||||
|
x2 |
- |
y 2 |
× 9 =1, далее т. M (6,-2 |
|
) лежит на гиперболе, т.е. |
36 |
- |
=1, |
||||||||||||||||||||||||||||||||||||
|
2 |
||||||||||||||||||||||||||||||||||||||||||||
|
a 2 |
4a 2 |
a2 |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4a 2 |
|||||||||
144 - 72 |
|
=1, |
|
72 = 4a2 , |
|
|
|
a2 =18, |
|
a = 3 |
|
; тогда b = |
2 |
× 3 |
|
|
= 2 |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
2 |
2 |
|
2 . Итак, |
|||||||||||||||||||||||||||||||||||||
|
|
4a2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
искомое уравнение |
x2 |
|
- |
y 2 |
=1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
18 |
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
- 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
3 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Рис. 7.
§ 5. Парабола. Каноническое уравнение параболы
Параболой называется множество точек плоскости, для которых расстояние до некоторой фиксированной точки F , называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой (не содержащей т. F ).
Пусть p – |
расстояние от F до директрисы. По определению параболы |
|
|
|||||||||||||||
|
|
|
|
|
= |
|
|
|
|
|
, |
|
|
|
|
(11) |
||
|
|
MF |
|
|
MN |
|
|
|
|
|
||||||||
где точка M – |
произвольная точка параболы, |
N – |
ее проекция на директрису. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
была фокусом, а x = - |
p |
|||
Выберем систему координат так, чтобы т. F |
|
,0 |
|
|
– |
|||||||||||||
2 |
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
директрисой.
10

y
N |
M(x,y) |
− |
p |
0 |
p |
|
x |
|
|
|
F |
|
,0 |
|
|
2 |
|
2 |
|
|||
|
|
|
|
|
||
Рис. 8.
Запишем соотношение (11) в координатах:
|
p |
2 |
2 |
|
|
p 2 |
||
x − |
|
|
+ y |
|
= |
x + |
|
|
|
|
|
||||||
|
2 |
|
|
|
|
2 |
||
это и есть уравнение параболы. После упрощения получим: y 2 = 2 px
Уравнение (13) называется каноническим уравнением параболы.
Основные характеристики параболы:
1.Парабола (13) симметрична относительно оси ox .
2.Точка O(0,0) – вершина параболы (13).
3.Фокальный радиус точки M(x,y) параболы: FM = x + p .
|
y2 = −2 px |
2 |
Уравнение вида |
(14) |
определяет параболу, для которой x ≤ 0 , т.е. график этой параболы:
y
M(x,y)
|
− |
p |
|
0 |
p |
x |
|
F |
|
,0 |
|
|
2 |
|
|
2 |
|
|
|||||
|
|
|
|
|
|
||
Рис. 9.
11
(12)
(13)

|
Уравнения вида |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
x2 |
= 2 py |
|
|
|
|
|
|
(15) |
|
|
|
|
|
|
|
|
|
|
x2 |
= -2 py |
|
|
|
|
|
|
(16) |
|
задают параболы симметричные относительно оси oy : |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
y |
|
|
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
p |
|
|
|
0 |
|
x |
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
F 0, |
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
2 |
|
M |
|
0,− |
p |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
0 |
|
x |
|
|
|
2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
p |
|
N |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
2 |
|
|
|
|
|
|
Рис. 11. |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Рис. 10. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
«Вырождения» параболы: |
|
|
|||||||
1. |
x2 |
= −k 2 , y 2 = -k 2 . Эти уравнения |
не определяют |
никакого точечного |
||||||||||||||
|
множества при k ¹ 0 . |
|
|
|
|
|
|
|
|
|
||||||||
2. |
x2 |
= k 2 , |
|
y2 |
= k 2 , эти уравнения определяют пару параллельных прямых: |
|||||||||||||
x = ±k и y = ±k . При k = 0 эти прямые совпадают.
Пример. Парабола, симметричная относительно оси oy , имеет вершину в начале координат и проходит через точку (6,-2). Написать уравнение параболы и определить координаты ее фокуса.
Решение. |
Уравнение параболы, симметричной относительно оси oy : |
x2 = 2 py либо x2 |
= -2 py . Подставим координаты точки в оба уравнения: |
62 ¹ 2 p × (- 2), т.к. p > 0 .
62 = -2 p × (- 2)
36 = 4 p p = 9
Уравнение параболы x2 = -18y , ветви вниз и F (0;−4,5)
12

y
0 |
6 |
x
-2
 F(0;-4,5)
F(0;-4,5)
Рис. 12.
§ 6. Применение преобразования координат к приведению уравнений кривых второго порядка к каноническому виду
Значения коэффициентов A, B,C общего уравнения |
(1) |
кривой |
II-го |
порядка Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0 определяют, |
к |
какому |
типу |
относится кривая (эллиптическому, гиперболическому или параболическому). Так, например, если A = C и B = 0 , то кривая – окружность или ее «вырождения». В общем случае, если:
A B
1.= AC − B2 > 0 , то кривая эллиптического вида.
B C
2.A B = AC − B2 < 0 , то кривая гиперболического вида.
B C
3.A B = AC − B2 = 0 , то кривая параболического вида.
B C
Спомощью преобразований параллельного переноса и поворота координатных осей общее уравнение кривой II-го порядка можно привести к каноническому виду.
Рассматриваются следующие преобразования координат:
1)параллельный перенос координатных осей:
y y′
M
′ |
x |
′ |
o (a,b) |
|
|
o |
|
x |
Рис. 13.
13
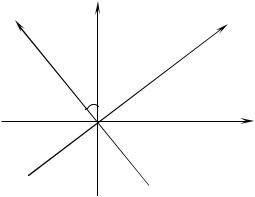
M (x, y) – точка с координатами в старой системе координат oxy , M (x′, y′) – точка с координатами в новой системе координат o′x′y′ ,
O′(a,b) – начало координат новой системы с координатами в старой системе.
x = x′ + a |
– формулы параллельного переноса координатных осей, |
|
|
y = y¢ + b |
|
выражающие старые координаты через новые.
x′ = x - a |
– обратные формулы. |
|
|
y¢ = y - b |
|
2) Поворот координатных осей на угол α :
y′ |
y |
x′ |
M |
α
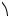 α
α
0 |
x |
Рис. 14.
M (x, y) – |
точка с координатами в старой системе координат oxy , |
|
|||
′ ′ |
) |
|
|
′ ′ ′ |
. |
M (x , y |
– точка с координатами в новой системе координат o x y |
||||
x = x′ × cosα - y′ × sinα |
– |
формулы преобразования координат т. M при |
|||
|
|
|
|||
y = x¢ × sinα + y¢ × cosα |
|
|
|
||
повороте осей на угол α . |
|
|
|
||
x′ = x × cosα + y × sinα |
– |
обратные формулы. |
|
||
|
|
|
|
||
y¢ = -x × sinα + y × cosα |
|
|
|
||
Пример 1. С помощью параллельного переноса осей координат привести к простейшему виду уравнение кривой x2 + 2 y2 − 4x + 8 y − 10 = 0 и построить ее.
Решение. AC - B2 = 2 > 0 – кривая эллиптического типа. Преобразуем
данное уравнение – сгруппируем полные квадраты x2 − 4x + 4 − 4 + 2(y 2 + 4 y + 4 − 4)− 10 = 0
(x - 2)2 + 2(y + 2)2 = 22
(x − 2)2 + (y + 2)2 = 1.
22 11
14

|
x − 2 = x′ |
эта система задает формулы параллельного переноса |
|||||||||
Положим |
+ 2 |
= y¢ |
|||||||||
|
y |
|
|
|
|
|
|
||||
осей координат |
в |
т. O (2,−2). Получим |
уравнение эллипса: |
x12 |
+ |
y12 |
=11, с |
||||
|
|
||||||||||
|
|
|
|
1 |
|
|
|
22 |
11 |
|
|
|
|
|
|
|
|
и центром симметрии в т.O1 (2,-2). |
|
||||
полуосями a = |
22 |
, b = |
11 |
|
|
|
|
||||
|
|
|
y |
0 |
|
y′ |
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
-a |
|
|
|
O1 |
|
|
|
|
|
|
|
|
|
|
a |
x′ |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
-b
Рис. 15.
Замечание. С помощью параллельного переноса координатных осей удается в общем уравнении избавиться от слагаемых, содержащих x и y в первой степени.
Пример 2. Преобразовать уравнение xy = m (m > 0) к простейшему виду.
Решение: AC - B2 = -1 < 0 – кривая гиперболического типа. Повернем заданную систему координат на угол α .
Подставим в заданное уравнение формулы
x = x′ × cosα - y′ × sinα |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
= x¢ × sinα + y¢ × cosα |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
y |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
(x′cosα - y′sinα )(x′sinα + y′cosα ) = m |
|
|
|
|
|
|||||||||||||||||||||||
|
x |
′2 |
cosα sinα - y |
′2 |
|
|
|
|
|
|
|
′ ′ |
2 |
α - sin |
2 |
α )= m |
||||||||||||
|
|
|
sinα cosα + x y (cos |
|
|
|||||||||||||||||||||||
cos2 α - sin2 α = 0 , |
|
cos 2α = 0 , |
2α = π , |
α = π . |
||||||||||||||||||||||||
Итак, при α = π |
|
|
|
|
|
|
|
|
2 |
|
4 |
|
|
|
||||||||||||||
мы избавились в уравнении от слагаемого, содержащего |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
произведение x′ × y′ и получили уравнение вида |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x¢2 |
× |
|
2 |
× |
|
|
2 |
- y¢2 × |
2 |
× |
|
2 |
= m |
или |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
2 |
|
|
2 |
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|||||
|
x′2 |
|
|
- |
y′2 |
|
=1 – это уравнение гиперболы с полуосями a = b = |
|
. |
|||||||||||||||||||
|
|
|
|
2m |
||||||||||||||||||||||||
|
2m |
|
||||||||||||||||||||||||||
|
|
|
2m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
15

y′ |
y |
x′ |
|

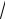 2m
2m

 2m
2m
О |
x |
- 
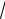 2m
2m
- 
 2m
2m
Рис. 16.
Замечание. С помощью поворота координатных осей удается избавиться от слагаемого, содержащего произведение xy .
Пример 3. Привести к простейшему виду и построить кривую, заданную
уравнением: |
x2 + 4x + 3y + 6 = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Решение. |
|
AC − B2 = 0 – кривая параболического типа. Выделим полный |
|||||||||||||||||||
квадрат |
и |
преобразуем |
|
данное уравнение: (x2 + 4x + 4)− 4 + 3y + 6 = 0 , |
|||||||||||||||||
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
x + 2 = x′ |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
(x + 2) |
= −3 y + |
|
|
. |
Положим, |
|
|
что |
|
2 |
= y′ |
являются |
формулами |
||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
y + |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
параллельного |
переноса в |
|
т. O |
− 2,− |
2 |
|
. Получим |
уравнение: |
x′2 = −3y′ – |
||||||||||||
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
3 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
− 2,− |
2 |
|
|
|
|
|
|
|
|
||||
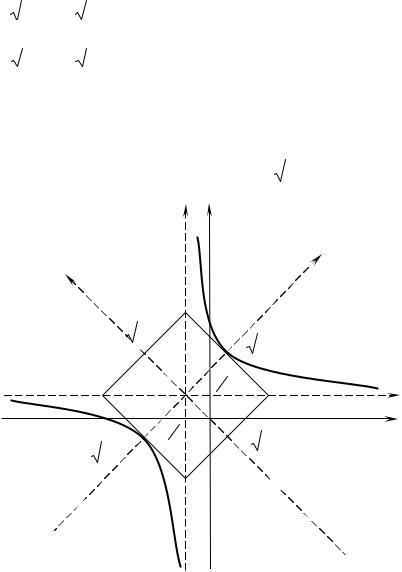
парабола с вершиной в т. O |
|
|
и симметричная относительно оси oy′ . |
||||||||||||||||||
3 |
|||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
y′ |
-2 |
y |
|
|
|
|
|
x |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
− |
2 |
|
|
|
x′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|||
1
-2
Рис. 17.
16
|
|
Пример 4. Построить кривую y = |
x + 3 |
. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x + 1 |
|
|
|
|||||||||||||||
|
|
Решение. Перепишем уравнение 2xy - x + y - 3 = 0 , 2x + 1 ¹ 0 . |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
AC - B2 = -4 < 0 – |
кривая гиперболического типа. |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Преобразуем данное уравнение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
2 y x + |
|
|
|
- |
x |
+ |
|
|
|
|
|
- |
|
|
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
1 |
|
= x¢ |
|
|
|
|||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
5 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||||||||||||||||||||
|
|
x + |
|
y - |
|
|
= |
|
|
|
, |
Положим |
|
|
|
|
|
|
|
|
|
. Получим x¢ × y¢ = |
|
. |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
y - |
|
1 |
= y¢ |
|
4 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
O¢ |
- |
|
, |
|
|
– новое начало координат после параллельного переноса. |
||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ ′ |
′ |
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
o |
(см. пример 2). |
||||||||
|
|
Повернем оси координат o x |
и o y |
|
|
на угол 45 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
x¢ = x¢¢ |
|
- y¢¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
y¢ = x¢¢ |
|
2 |
|
- y¢¢ |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Получим уравнение (x¢¢)2 × |
1 |
- (y¢¢)2 |
× |
1 |
= |
5 |
, |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
′′ |
|
|
|
|
|
|
|
′′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
4 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
(x |
) |
− (y |
|
|
= 1 – |
|
|
гипербола, где |
a = b = 2,5 . |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
) |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2,5 |
|
|
2,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y′ |
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y′′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x′′ |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2,5 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O′ |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x′ |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 1 |
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
x |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2,5 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Рис. 18.
17

Задание 1
1.01. Составить уравнение эллипса, имеющего общие фокусы с
гиперболой x2 − 2 y 2 = 24 , если эксцентриситет равен 3 .
5
1.02. Найти расстояние от центра окружности x2 + y 2 + 6x + 2 y − 5 = 0 до асимптот гиперболы 9x2 − 16 y 2 = 144 .
1.03. На параболе y2 = 32x взяты две точки M 1 и M 2 , расстояния которых до фокуса этой параболы равны 10. Составить уравнение окружности, диаметром которой является отрезок M 1 M 2 .
1.04. Вершины эллипса, большая ось которого лежит на оси абсцисс, совпадают с вершинами равносторонней гиперболы. Составить уравнения обеих кривых, если известно, что точка M (6, 2), лежащая на гиперболе, равноудалена от ближайших к ней фокусов эллипса и гиперболы.
1.05. Ось симметрии параболы параллельна оси ординат, а уравнение директрисы y − 10 = 0 . Составить уравнение параболы, если она пересекает ось
ox в точках (− 5,0) и (11, 0). |
|
|
|
|
|
|
|
|
|
1.06. Вершина параболы совпадает с одним |
из |
фокусов гиперболы |
|||||||
9x2 − 16 y 2 = 144 . |
Составить |
уравнение |
параболы, |
если |
известно, |
что |
ее |
||
директриса проходит через точки (− 4,−3) и (− 4,3). |
|
|
|
|
|
|
|||
1.07. Директриса параболы пересекает эллипс |
9x2 + 20 y 2 |
= 324 |
в точках |
||||||
(− 4,3) и (4,3), |
|
|
|
||||||
а расстояние от этих точек до фокуса параболы равно 2 |
5 . |
||||||||
Составить уравнение параболы. |
x2 − y 2 = 16 |
|
|
|
|
|
|
||
1.08. Равносторонняя |
гипербола |
проходит |
через |
фокусы |
|||||
эллипса. Составить простейшее уравнение этого эллипса, если отношение эксцентриситетов гиперболы и эллипса равно 
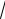 3 .
3 .
1.09. Найти длину стороны квадрата, вписанного в эллипс
9x2 + 16 y 2 = 576 .
1.10. Найти угол, под которым из фокуса параболы x2 − 4x + 8y − 20 = 0
видна большая ось эллипса x2 + 2 y 2 = 16 .
1.11.Написать каноническое уравнение эллипса, если его большая ось равна 16 , а фокусы отстоят от вершин на 0, 2 от ее длины.
1.12.Меридиан земного шара имеет форму эллипса, отношение осей
которого равно 299 . Определить эксцентриситет земного меридиана. 300
1.13. Написать уравнение окружности, проходящей через точки (− 1, 2) и (3, 0), зная, что ее центр лежит на прямой x − y + 2 = 0 .
18

1.14.Написать уравнение гиперболы, имеющей общие фокусы с эллипсом
x2 + y 2 = 1 , если ее эксцентриситет равен 1, 25 .
4924
1.15.На эллипсе x2 + y 2 = 1 найти точку, отстоящую на расстояние пяти
30 24
единиц от его малой оси.
1.16. Прямые x = 8, x = −8 служат директрисами эллипса, малая ось которого равна 8 . Найти уравнение этого эллипса.
1.17. Эллипс проходит через точки M (
 3,−2) и N (− 2
3,−2) и N (− 2
 3,1). Составить уравнение эллипса, приняв его оси за оси координат.
3,1). Составить уравнение эллипса, приняв его оси за оси координат.
1.18. Составить уравнение гиперболы, проходящей через точку A(9,−8),
если асимптоты ее заданы уравнениями 
 2x ± 3y = 0 .
2x ± 3y = 0 .
1.19.Написать каноническое уравнение параболы с вершиной в начале
координат, если известно, что ее фокус находится в точке пересечения прямой
4x − 3y − 4 = 0 с осью ox .
1.20.Написать уравнение окружности, центр которого находится в правом
фокусе гиперболы x2 − y 2 = 1, а радиус равен расстоянию между фокусами этой
25 16
гиперболы.
1.21. Струя воды, выбрасываемая фонтаном, принимает форму параболы, параметр которой p = 0,1. Определить высоту струи, если известно, что она падает в бассейн на расстоянии 2 метра от места выхода.
1.22. Фокусы гиперболы совпадают с фокусами эллипса x2 + y 2 = 1.
16 25
Составить уравнение гиперболы, если ее эксцентриситет равен 1,5 .
1.23. Найти уравнение гиперболы, вершины которой находятся в фокусах
эллипса |
x2 |
+ |
y 2 |
= 1, а фокусы гиперболы |
находятся в вершинах данного |
|
|
||||
16 |
25 |
|
|
||
эллипса. |
|
|
|
|
|
1.24. Найти уравнение окружности, |
симметричной с окружностью |
||||
x2 + y 2 = 9 относительно прямой x − y = 6 . |
|
||||
1.25. Найти уравнение эллипса, вершины которого находятся в фокусах гиперболы x2 − y 2 = 1, а фокусы в вершинах данной гиперболы.
1625
1.26.Определить угол между асимптотами гиперболы, если расстояние между фокусами вдвое больше расстояния между директрисами.
1.27.Мостовая арка имеет форму параболы. Определить параметр этой параболы, зная, что пролет арки равен 24м, а высота 6м.
1.28.Через точку M (2,−5) провести прямые, параллельные асимптотам
гиперболы x2 − 4 y2 = 4 .
19
