книги / Экономические задачи линейного программирования и их решение с использованием Microsoft Excel

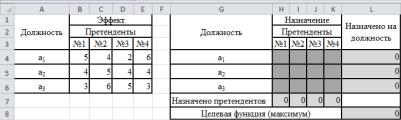
z= 5x11 + 4x12 + 2x13 + 6x14 + 4x21 + 5x22 +

+4x23 + 4x24 + 3x31 + 6x32 + 5x33 + 3x34 → max.

Асистема ограничений примет вид

x11 x21 x31 1;x12 x22 x32 1;

x13 x23 x33 1;x14 x24 x34 1;

x11 x12 x13 x14 1;x21 x22 x23 x24 1;x31 x32 x33 x34 1,

где xij – булевы переменные.

Решение

На рабочий лист Excel введем исходные данные и таблицу с изменяемыми ячейками (рис. 3.3.1).

Рис. 3.3.1. Исходные данные и таблица с изменяемыми ячейками

Ячейки H4:K6 предназначены для значений переменных (это изменяемые в процессе поиска решения ячейки), в которых появятся значения 0 или 1 по завершении поиска решения.

L8 – целевая ячейка, в которой будет размещена формула целевой функции.

91

В таблице Назначение добавлены:

–столбец Назначено на должность;

–строка Назначено претендентов.

Заполним таблицу Назначение формулами:

–ограничения на должности – в ячейку L4 столбца введем =СУММ(H4:K4), а затем растянем эту формулу

вячейки L5:L6;

–ограничения на претендентов – в ячейку H7 =СУММ(H4:H6) и растянем ее в ячейки I7:K7;

–в ячейку L8 запишем формулу для целевой функции

=СУММПРОИЗВ(B4:E6;H4:K6).

Для поиска оптимального решения воспользуемся надстройкой Поиск решения. Заполним диалоговое окно надстройки (рис. 3.3.2):

1. В поле Оптимизировать целевую ячейку введите

адрес ЦФ L8.

2.Ниже выберите параметр Максимум.

3.В поле Изменяя ячейки переменных введите диапа-

зон ячеек с искомыми переменными H4:K6.

4.Установите флажок Сделать переменные без ограничений неотрицательными и выберите параметр Поиск решения линейных задач симплекс-методом.

5.Щелчком по кнопке Добавить вызовите окно Добавление ограничения. В этом окне выполните ссылки на ячейки ограничений, а также выберите оператор ограничений. Для решения данной задачи нам необходимы следующие ограничения:

– L4:L6 = 1 – условие назначения на все должности;

– H7:K7 ≤ 1 – условие распределения претендентов;

– H4:K6 – бинарные переменные.

6.Нажав кнопку Найти решения, получим результаты решения.

92

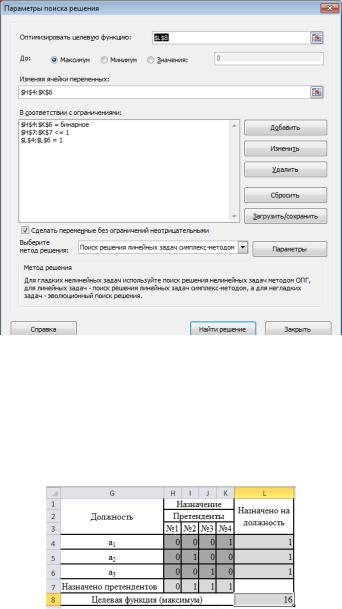
Рис. 3.3.2. Диалоговое окно Поиск решения

Вокне Результаты поиска решения выберем отчет

исохраним полученный результат как сценарий (кнопка

Сохранить сценарии) с именем Назначение.

На рис. 3.3.3 приведено оптимальное назначение на должность.

Рис. 3.3.3. Результаты выполнения поиска решения

93

Анализ отчетов

Отчет о результатах

Значение целевой функции z(x)min = 16. Значение переменных:

Таким образом, анализ решения показал, что:

–претендент № 1 остается без работы;

–претендент № 2 назначен на должность а2;

–претендент № 3 назначен на должность а3;

–претендент № 4 назначен на должность а1.

3.4.Оптимальный раскрой материала

Вданном параграфе рассмотрены возможности использования модели линейного программирования для решения задач раскроя. Эта область приложения модели линейного программирования хорошо изучена. Благодаря работам в области оптимального раскроя основоположника теории линейного программирования лауреата Нобелевской премии академика Л.В. Канторовича задачу оптимального раскроя можно назвать классической прикладной оптимизационной задачей.

Большинство материалов, используемых в промышленности, поступает на производство в виде стандартных форм. Непосредственное использование таких материалов, как правило, невозможно. Предварительно их разделяют на заготовки необходимых размеров. Это можно сделать, используя различные способы раскроя материала. Задача оптимального раскроя состоит в том, чтобы выбрать один

94

или несколько способов раскроя материала и определить, какое количество материала следует раскраивать, применяя каждый из выбранных способов. Задачи такого типа возникают в металлургии и машиностроении, лесной, лесообрабатывающей, легкой промышленности.

Задача рационального или оптимального раскроя (распила) материалов возникает в заготовительном цехе любого машиностроительного предприятия. Рациональный раскрой материалов на заготовки позволяет экономить сырье, уменьшая отходы. А это, в свою очередь, приводит к снижению себестоимости продукции.

Выделяют два этапа решения задачи оптимального раскроя. На первом этапе определяются рациональные способы раскроя материала, на втором решается задача линейного программирования для определения интенсивности использования рациональных способов раскроя.

Обычно в задачах подобного типа не задаются способы раскроя, их определяет разработчик-специалист из практических соображений до построения математической модели.

1. Определение рациональных способов раскроя ма-

териала. В задачах оптимального раскроя рассматриваются так называемые рациональные (оптимальные по Парето) способы раскроя. Предположим, что из единицы материала можно изготовить заготовки нескольких видов. Способ раскроя единицы материала называется рацио-

нальным (оптимальным по Парето), если увеличение числа заготовок одного вида возможно только за счет сокращения числа заготовок другого вида.

95

Если способ раскроя задан, то известно количество заготовок, полученных из единицы конкретного вида материала.

2. Определение интенсивности использования рациональных способов раскроя. Обозначения:

j – индекс материала, j = 1,..., п;

k – индекс вида заготовки, k = 1, ..., q;

i – индекс способа раскроя единицы материала, i = = 1,..., р;

аijk – количество (целое число) заготовок вида k, полученных при раскрое единицыj-го материала i-м способом; bk – число заготовок вида k в комплекте, поставляе-

мом заказчику;

Bk – план выпуска заготовки k-го вида; dj – количество материала j-го вида;

cji – величина отхода, полученного при раскрое единицы j-го материала по i-му способу;

w – число комплектов заготовок различного вида, поставляемых заказчику;

xji – количество единиц j-го материала, раскраиваемых по i-му способу (интенсивность использования способа раскроя).

Математическая модель задачи раскроя с минимальным расходом материалов примет вид

96

(3.4.1) – целевая функция (минимум количества используемых материалов);

(3.4.2)–(3.4.3) – система ограничений, определяющих количествозаготовок, необходимоедля выполнения заказа;

(3.4.4) – условия неотрицательности переменных. Математическая модель задачи раскроя с минималь-

ными отходами примет вид

при условиях (3.4.2)–(3.4.4).

Математическая модель задачи раскроя с учетом комплектации примет вид

(3.4.6) – целевая функция (максимум комплектов, включающих заготовки различных видов);

(3.4.7) – ограничения по количеству материалов; (3.4.8) – система ограничений, определяющих количест-

возаготовок, необходимоедляформированиякомплектов; (3.4.9) – условия неотрицательности переменных.

97

Пример решения задачи в Microsoft Excel

Постановка задачи

Прутки длинной L1 = 100 см в количестве 50 шт. и длинной L2 = 150 см в количестве 60 шт. требуется разрезать на заготовки длинной l1 = 40, l2 = 35 и l3 = 45 см.

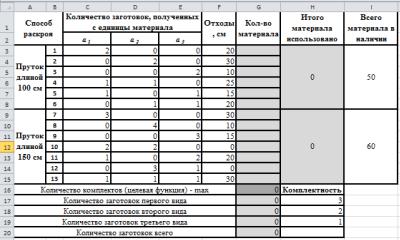
Необходимо построить таблицу полноценных вариантов раскроя (табл. 3.4.1).

На множестве полноценных вариантов раскроя сформулировать модель задачи по критериям максимума количества заготовок, удовлетворяющих условию комплектности (3, 2, 1). Найти оптимальный план раскроя. Проанализировать решение.

Варианты раскроя

Таблица 3.4.1 Таблица полноценных вариантов раскроя

98

Моделирование

Обозначим переменные величины:

х1 – количество первого материала, раскроенного первым способом;

х2 – количество первого материала, раскроенного вторым способом;

х3 – количество первого материала, раскроенного третьим способом;

х4 – количество первого материала, раскроенного четвертым способом;

х5 – количество первого материала, раскроенного пятым способом;

х6 – количество первого материала, раскроенного шестым способом;

х7 – количество второго материала, раскроенного седьмым способом;

х8 – количество второго материала, раскроенного восьмым способом;

х9 – количество второго материала, раскроенного девятым способом;

х10 – количество второго материала, раскроенного десятым способом;

х11 – количество второго материала, раскроенного одиннадцатым способом;

х12 – количество второго материала, раскроенного двенадцатым способом;

х13 – количество второго материала, раскроенного тринадцатым способом;

w – количество комплектов.

Тогда целевая функция z = w → max – максимум комплектов при условиях

99

xi ≥ 0, i = 1, 2, …, 18.

Решение

На рабочий лист Excel введем исходные данные и таблицу с изменяемыми ячейками (рис. 3.4.1).

Рис. 3.4.1. Исходные данные и таблица с изменяемыми ячейками

Ячейки G3:G15 предназначены для значений переменных.

G16 – целевая ячейка, в которой будет размещена формула целевой функции.

100