
книги / Механика сплошных сред (теоретические основы обработки давлением композитных материалов с задачами и решениями, примерами и упражнениями)
..pdf
1.2. КИНЕМАТИКА
Продолжение вариантов ДЗ № 2 по пункту А
Вариант
Группа 4
Вариант
Вариант
Вариант
Вариант
Вариант
Вариант
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
E |
1 |
=L |
+0,1L |
(еt–1); |
E |
1 |
=L |
+0,2L |
(еt–1); |
L |
1 |
=E |
+0,1E |
(еt–1); |
L |
1 |
=E |
+0,2E |
(еt–1); |
||||||
E |
1 |
2 |
(1–еt); |
E |
1 |
|
|
|
2 |
(1–еt); |
L |
1 |
2 |
(1–еt); |
L |
1 |
|
|
|
2 |
(1–еt); |
||||
2 |
=L |
+0,1L |
2 |
=L |
+0,2L |
2 |
=E |
+0,1E |
2 |
=E |
+0,2E |
||||||||||||||
|
2 |
1 |
|
|
2 |
|
|
|
1 |
|
|
2 |
1 |
|
|
2 |
|
|
|
1 |
|
||||
E3=L3 |
|
|
E3=L3 |
|
|
|
|
|
L3=E3 |
|
|
L3=E3 |
|
|
|
|
|
||||||||
|
|
|
5 |
|
|
|
|
|
6 |
|
|
|
|
|
|
7 |
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
E |
1 |
=L |
+0,3L |
(еt–1); |
E |
1 |
=L |
+0,4L |
(еt–1); |
L |
1 |
=E |
+0,3E |
(еt–1); |
L |
1 |
=E |
+0,4E |
(еt–1); |
||||||
E |
1 |
2 |
(1–еt); |
E |
1 |
|
|
|
2 |
(1–еt); |
L |
1 |
2 |
(1–еt); |
L |
1 |
|
|
|
2 |
(1–еt); |
||||
2 |
=L |
+0,4L |
2 |
=L |
+0,4L |
2 |
=E |
+0,3E |
2 |
=E |
+0,4E |
||||||||||||||
|
2 |
1 |
|
|
2 |
|
|
|
1 |
|
|
2 |
1 |
|
|
2 |
|
|
|
1 |
|
||||
E3=L3 |
|
|
E3=L3 |
|
|
|
|
|
L3=E3 |
|
|
L3=E3 |
|
|
|
|
|
||||||||
|
|
|
9 |
|
|
|
|
|
10 |
|
|
|
|
|
11 |
|
|
|
|
|
12 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
E |
1 |
=L |
+0,5L |
(еt–1); |
E |
1 |
=L |
+0,6L |
(еt–1); |
L |
1 |
=E |
+0,5E |
(еt–1); |
L |
1 |
=E |
+0,6E |
(еt–1); |
||||||
E |
1 |
2 |
(1–еt); |
E |
1 |
|
|
|
2 |
(1–еt); |
L |
1 |
2 |
(1–еt); |
L |
1 |
|
|
|
2 |
(1–еt); |
||||
2 |
=L |
+0,5L |
2 |
=L |
+0,6L |
2 |
=E |
+0,5E |
2 |
=E |
+0,6E |
||||||||||||||
|
2 |
1 |
|
|
2 |
|
|
|
1 |
|
|
2 |
1 |
|
|
2 |
|
|
|
1 |
|
||||
E3=L3 |
|
|
E3=L3 |
|
|
|
|
|
L3=E3 |
|
|
L3=E3 |
|
|
|
|
|
||||||||
|
|
|
13 |
|
|
|
|
|
14 |
|
|
|
|
|
15 |
|
|
|
|
|
16 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
E |
1 |
=L |
+0,7L |
(еt–1); |
E |
1 |
=L |
+0,8L |
(еt–1); |
L |
1 |
=E |
+0,7E |
(еt–1); |
L |
1 |
=E |
+0,8E |
(еt–1); |
||||||
E |
1 |
3 |
(1–еt); |
E |
1 |
|
|
|
2 |
(1–еt); |
L |
1 |
3 |
(1–еt); |
L |
1 |
|
|
|
2 |
(1–еt); |
||||
2 |
=L |
+0,7L |
2 |
=L |
+0,8L |
2 |
=E |
+0,7E |
2 |
=E |
+0,8E |
||||||||||||||
|
2 |
1 |
|
|
2 |
|
|
|
3 |
|
|
2 |
1 |
|
|
2 |
|
|
|
3 |
|
||||
E3=L3 |
|
|
E3=L3 |
|
|
|
|
|
L3=E3 |
|
|
L3=E3 |
|
|
|
|
|
||||||||
|
|
|
17 |
|
|
|
|
|
18 |
|
|
|
|
|
19 |
|
|
|
|
|
20 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
E |
1 |
=L |
+0,9L |
(еt–1); |
E |
1 |
= L |
1 |
+ L |
2 |
( е t – 1 ) ; |
L |
1 |
=E |
+0,9E |
(еt–1); |
L |
1 |
= E |
1 |
+ E |
2 |
( е 2 t – 1 ) ; |
||
E |
1 |
2 |
(1–еt); |
E |
= L |
+ L |
( 1 – е t ) ; |
L |
1 |
2 |
(1–еt); |
L |
= E |
+ E |
( 1 – е 2 t ) ; |
||||||||||
2 |
=L |
+0,9L |
2 |
2 |
1 |
2 |
=E |
+0,9E |
2 |
2 |
1 |
||||||||||||||
|
2 |
1 |
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
||||||||
E3=L3 |
|
|
E3=L3 |
|
|
|
|
|
L3=E3 |
|
|
L3=E3 |
|
|
|
|
|
||||||||
|
|
|
21 |
|
|
|
|
|
22 |
|
|
|
|
|
23 |
|
|
|
|
|
24 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
E |
1 |
=L |
+1,1L |
(еt–1); |
E |
1 |
=L |
+1,2L |
(еt–1); |
L |
1 |
=E |
+1,1E |
(еt–1); |
L |
1 |
=E |
+1,2E |
(еt–1); |
||||||
E |
1 |
2 |
(1–еt); |
E |
1 |
|
|
|
2 |
(1–еt); |
L |
1 |
2 |
(1–еt); |
L |
1 |
|
|
|
2 |
(1–еt); |
||||
2 |
=L |
+1,1L |
2 |
=L |
+1,2L |
2 |
=E |
+1,1E |
2 |
=E |
+1,2E |
||||||||||||||
|
2 |
1 |
|
|
2 |
|
|
|
1 |
|
|
2 |
1 |
|
|
2 |
|
|
|
1 |
|
||||
E3=L3 |
|
|
E3=L3 |
|
|
|
|
|
L3=E3 |
|
|
L3=E3 |
|
|
|
|
|
||||||||
|
|
|
25 |
|
|
|
|
|
26 |
|
|
|
|
|
27 |
|
|
|
|
|
28 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
E |
1 |
=L |
+1,3L |
(еt–1); |
E |
1 |
=L |
+1,4L |
(еt–1); |
L |
1 |
=E |
+1,3E |
(еt–1); |
L |
1 |
=E |
+1,4E |
(еt–1); |
||||||
E |
1 |
2 |
(1–еt); |
E |
1 |
|
|
|
2 |
(1–еt); |
L |
1 |
2 |
(1–еt); |
L |
1 |
|
|
|
2 |
(1–еt); |
||||
2 |
=L |
+1,3L |
2 |
=L |
+1,4L |
2 |
=E |
+1,3E |
2 |
=E |
+1,4E |
||||||||||||||
|
2 |
1 |
|
|
2 |
|
|
|
1 |
|
|
2 |
1 |
|
|
2 |
|
|
|
1 |
|
||||
E3=L3 |
|
|
E3=L3 |
|
|
|
|
|
L3=E3 |
|
|
L3=E3 |
|
|
|
|
|
||||||||
Пункт Б ДЗ № 2. По заданной функции тока ψ(x1; x2) определить: 1) поле скоростей; 2) компоненты тензора скоростей деформаций; 3) интенсивность сдвиговых деформаций; 4) степень деформации сдвига.
Варианты ДЗ № 2 по пункту Б |
|
|
|
|
|
|
|
|
|
||||
Вариант |
|
1 |
|
2 |
|
|
3 |
|
|
4 |
|
|
|
Группа 1 |
ψ = ln |
x2 |
+ x3 |
ψ = arctg(x |
/x |
) |
ψ = sinx |
chx |
2 |
ψ = sinx |
2 |
chx |
1 |
|
1 |
2 |
2 |
1 |
|
1 |
|
|
|
||||
Вариант |
|
5 |
|
6 |
|
|
7 |
|
|
8 |
|
|
|
|
ψ = cosx1shx2 |
ψ = cosx2shx1 |
|
ψ =sinx1cosx2 |
ψ = sinx2cosx1 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
131 |

1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД
Продолжение вариантов ДЗ № 2 по пункту Б
Вариант |
9 |
|
|
|
|
10 |
|
|
|
|
|
11 |
|
|
|
|
|
12 |
|
|
|
|
|
|||||
|
ψ = sinx1shx2 |
|
|
ψ = sinx2shx1 |
|
|
ψ = cosx1chx2 |
|
ψ = cosx2chx1 |
|
||||||||||||||||||
Вариант |
13 |
|
|
|
|
14 |
|
|
|
|
|
15 |
|
|
|
|
|
16 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
ψ =cosx1cosx2 |
|
ψ = sinx2sinx1 |
|
ψ = chx1chx2 |
|
|
|
ψ = shx2shx1 |
|
|
|
||||||||||||||||
Вариант |
17 |
|
|
|
|
18 |
|
|
|
|
|
19 |
|
|
|
|
|
20 |
|
|
|
|
|
|||||
|
ψ = chx1shx2 |
|
|
ψ = chx2shx1 |
|
|
ψ = sinx1/chx2 |
ψ = sinx2/chx1 |
||||||||||||||||||||
Вариант |
21 |
|
|
|
|
22 |
|
|
|
|
|
23 |
|
|
|
|
|
24 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
ψ = chx1/sinx2 |
|
ψ = chx2/sinx1 |
ψ = sinx1/shx2 |
|
ψ = sinx2/shx1 |
|
|||||||||||||||||||||
Вариант |
25 |
|
|
|
|
26 |
|
|
|
|
|
27 |
|
|
|
|
|
28 |
|
|
|
|
|
|||||
|
ψ =cosx1/chx2 |
|
ψ = cosx2/chx1 |
ψ = shx1/sinx2 |
|
ψ = shx2/sinx1 |
|
|||||||||||||||||||||
Вариант |
1 |
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|||
Группа 2 |
ψ = tgx1thx2 |
|
|
ψ = tgx2thx1 |
|
|
ψ = tgx1cthx2 |
|
|
ψ = tgx2cthx1 |
|
|
||||||||||||||||
Вариант |
5 |
|
|
|
|
6 |
|
|
|
|
|
|
7 |
|
|
|
|
|
|
8 |
|
|
|
|
|
|||
|
ψ = ctgx1thx2 |
|
|
ψ = ctgx2thx1 |
|
|
ψ = sinx1thx2 |
|
|
ψ = sinx2thx1 |
|
|
||||||||||||||||
Вариант |
9 |
|
|
|
|
10 |
|
|
|
|
|
11 |
|
|
|
|
|
12 |
|
|
|
|
|
|||||
|
ψ = cosx1thx2 |
|
|
ψ = cosx2thx1 |
|
|
ψ = shx1tgx2 |
|
|
|
ψ = shx2tgx1 |
|
|
|
||||||||||||||
Вариант |
13 |
|
|
|
|
14 |
|
|
|
|
|
15 |
|
|
|
|
|
16 |
|
|
|
|
|
|||||
|
ψ = chx1tgx2 |
|
|
ψ = chx2tgx1 |
|
|
ψ = sinx1cthx2 |
|
ψ = sinx2cthx1 |
|
||||||||||||||||||
Вариант |
17 |
|
|
|
|
18 |
|
|
|
|
|
19 |
|
|
|
|
|
20 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
ψ = cosx1cthx2 |
|
ψ = cosx2cthx1 |
ψ = shx1ctgx2 |
|
|
ψ = shx2ctgx1 |
|
|
|||||||||||||||||||
Вариант |
21 |
|
|
|
|
22 |
|
|
|
|
|
23 |
|
|
|
|
|
24 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
ψ = chx1ctgx2 |
|
|
ψ = chx2ctgx1 |
|
|
ψ = tgx1/shx2 |
|
|
ψ = tgx2/shx1 |
|
|
||||||||||||||||
Вариант |
25 |
|
|
|
|
26 |
|
|
|
|
|
27 |
|
|
|
|
|
28 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ψ = tgx1/chx2 |
|
|
ψ = tgx2/chx1 |
|
|
ψ = thx1/sinx2 |
|
ψ = thx2/sinx1 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Вариант |
1 |
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Группа 3 |
ψ = thx |
/cosx |
2 |
|
ψ = thx |
/cosx |
1 |
ψ = sin2x |
1 |
chx |
2 |
|
ψ = sin2x |
2 |
chx |
1 |
|
|||||||||||
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Вариант |
5 |
|
|
|
|
6 |
|
|
|
|
|
|
7 |
|
|
|
|
|
|
8 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ψ = cos2x |
1 |
shx |
2 |
|
ψ = cos2x |
2 |
shx |
1 |
ψ = sin2x |
1 |
cosx |
2 |
ψ = sin2x |
2 |
cosx |
1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Вариант |
9 |
|
|
|
|
10 |
|
|
|
|
|
11 |
|
|
|
|
|
12 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ψ = sin2x1shx2 |
|
ψ = sin2x2shx1 |
ψ = cos2x1chx2 |
ψ = cos2x2chx1 |
|||||||||||||||||||||||
Вариант |
13 |
|
|
|
|
14 |
|
|
|
|
|
15 |
|
|
|
|
|
16 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
ψ = cos2x |
1 |
cosx |
2 |
ψ = sin2x |
2 |
sinx |
1 |
ψ = ch2x |
|
chx |
2 |
|
ψ = sh2x |
2 |
shx |
1 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||
132

1.2. КИНЕМАТИКА
Продолжение вариантов ДЗ № 2 по пункту Б
Вариант |
17 |
|
|
18 |
|
|
19 |
|
|
20 |
|
|
||||
Группа 3 |
ψ = ch2x |
1 |
shx |
2 |
ψ = ch2x |
2 |
shx |
1 |
ψ = sin2x |
1 |
/chx |
2 |
ψ = sin2x |
2 |
/chx |
1 |
Вариант |
21 |
|
|
22 |
|
|
23 |
|
|
24 |
|
|
||||
|
ψ = ch2x1/sinx2 |
ψ = ch2x2/sinx1 |
ψ = sin2x1/shx2 |
ψ = sin2x2/shx1 |
||||||||||||
Вариант |
25 |
|
|
26 |
|
|
27 |
|
|
28 |
|
|
||||
|
ψ = cos2x1/chx2 |
ψ = cos2x2/chx1 |
ψ = sh2x1/sinx2 |
ψ = sh2x2/sinx1 |
||||||||||||
Вариант |
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
||||||||||
Группа 4 |
ψ = tg2x1thx2 |
ψ = tg2x2thx1 |
ψ = tgx1cthx3 |
|
ψ = tgx2cthx3 |
|
||||||||||
Вариант |
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
ψ = ctgx1thx3 |
ψ = ctgx2thx3 |
ψ = sinx1thx3 |
|
ψ = sinx2thx3 |
|
||||||||||
Вариант |
9 |
|
|
|
10 |
|
|
11 |
|
|
12 |
|
|
|||
|
ψ = cosx1thx3 |
ψ = cosx2thx3 |
ψ = shx1tgx3 |
|
ψ = shx2tgx3 |
|
||||||||||
Вариант |
13 |
|
|
14 |
|
|
15 |
|
|
16 |
|
|
||||
|
ψ = chx1tgx3 |
|
ψ = chx2tgx3 |
|
ψ = sinx1cthx3 |
|
ψ = sinx2cthx3 |
|
||||||||
Вариант |
17 |
|
|
18 |
|
|
19 |
|
|
20 |
|
|
||||
|
ψ = cosx1cthx3 |
ψ = cosx2cthx3 |
ψ = shx1ctgx3 |
|
ψ = shx2ctgx3 |
|
||||||||||
Вариант |
21 |
|
|
22 |
|
|
23 |
|
|
24 |
|
|
||||
|
ψ = chx1ctgx3 |
ψ = chx2ctgx3 |
ψ = tgx1/shx3 |
|
ψ = tgx2/shx3 |
|
||||||||||
Вариант |
25 |
|
|
26 |
|
|
27 |
|
|
28 |
|
|
||||
|
ψ = tgx1/chx3 |
ψ = tgx2/chx3 |
ψ = thx1/sinx3 |
|
ψ = thx2/sinx3 |
|
||||||||||
Типовые варианты контрольной работы № 2 по разделу МСС «Кинематика»
Иллюстративный вариант
А.Запишите в общем виде закон сохранения материальных частиц в лагранжевых координатах.
Б.Какой физический смысл якобиана преобразования лагранжевых координат в эйлеровы координаты? В каком случае он равен единице?
В.По заданному закону движения в лагранжевых координатах E1 = L1; E2 = L2et; E3 = L3e–t записать его в эйлеровых координатах.
Г.Для закона движения в п. В определить поля перемещений и скоростей в лагранжевых координатах.
Д.По найденному в п. Г полю скоростей определить поле тензора скоростей деформаций.
133

1.МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД
Е.Используя результаты пунктов В...Д, определить, куда переместится центр элементарного куба, первоначально (t = 0) находившегося в точке М(1, 1, 2), к моменту времени t = 1. Охарактеризовать и изобразить характер изменения во времени размеров, формы и объема куба.
Ответы по пунктам иллюстративного варианта
А.В связи с совпадением в лагранжевых координатах Li полной и частной производных по времени t закон сохранения материальных частиц
dLdt = 0 в этих координатах имеет вид ∂∂Lt = 0.
Б. Якобиан JL = |
∂E |
|
∂Li |
характеризует в лагранжевых координатах изменение |
|
|
k |
|
объема в окрестности материальной частицы; он равен единице при неизменном объеме этой окрестности.
В. Закон движения в эйлеровых координатах имеет вид
L1 = E1; L2 = E2e–t; L3 = E3et.
Г. В лагранжевых координатах вектор перемещения U имеет компоненты
U1 = 0; U2 = L2(et– 1); U3 = L3(e–t – 1),
вектор скорости V имеет компоненты
V1 = 0; V2 = L2et; V3 = –L3e–t.
Д.По формуле Дж. Стокса компоненты тензора скоростей деформаций определяются в эйлеровых координатах. Поэтому, используя результаты решений пунктов В и Г, сначала находим компоненты вектора скорости
V в эйлеровых координатах:
V1 = 0; V2 = E2; V3 = –E3.
Тогда компоненты тензора скоростей деформаций ξ22 = 1, ξ33 = –1 и ос-
тальные компоненты равны нулю, а сам тензор имеет вид Tξ = |
1 |
0 |
. |
|
0 |
−1 |
|||
|
|
134
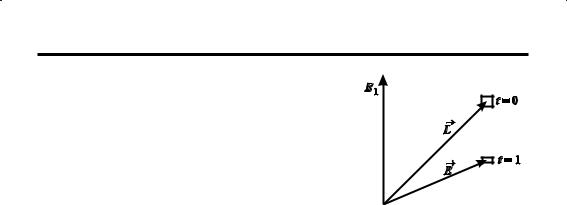
1.2. КИНЕМАТИКА
Е. В начальный момент времени t0 = 0 центр эле-
ментарного куба имеет координаты L1 = 1; L2 = 1; L3 = 2, а к моменту времени t = 1 коор-
динаты этого центра имеют вид E1 = 1; E2 = e; E3 = 2e–1 (рис. 36). В п. Д определено, что
[22 > 0 и [33 < 0, а тензор скорости жесткого поворота Tw = 0, поэтому в направлении вто-
рой оси происходит удлинение элементарно-  го волокна, а в направлении третьей оси про-
го волокна, а в направлении третьей оси про- 
 исходит сжатие элементарного волокна. Все Рис. 36. Схема к решению п. Д боковые компоненты тензора скоростей деформаций равны нулю. Поэтому элементарный куб преобразовывается в
исходит сжатие элементарного волокна. Все Рис. 36. Схема к решению п. Д боковые компоненты тензора скоростей деформаций равны нулю. Поэтому элементарный куб преобразовывается в
элементарный прямоугольный параллелепипед. Равенство нулю объемной скорости деформации [= [11 + [22 + [33 свидетельствует о том, что элементарное тело движется без изменения объема.
Вариант 1 А. Что называется вектором скорости?
Б.Каков физический смысл диагональных компонент тензоров конечных деформаций Г. Грина и Ж. Лагранжа?
В.По заданному закону движения в лагранжевых координатах E1 = L1et; E2 = L2e–t; E3 = L3 записать его в эйлеровых координатах.
Г.Для закона движения в п. В определить поля перемещений и скоростей в лагранжевых координатах.
Д.По найденному в п. Г полю скоростей определить поле тензора скоростей деформаций.
Е.Используя результаты пунктов В...Д, определить, куда переместится центр элементарного куба, первоначально (t = 0) находившегося в точке М(2, 2, 2), к моменту времени t = 1. Охарактеризовать и изобразить характер изменения во времени размеров, формы и объема куба.
Вариант 2
А.Каков физический смысл первого инварианта тензора малых деформаций?
Б. Как вычислить скорость по заданному в эйлеровых координатах закону движения?
В.По заданному закону движения в лагранжевых координатах E1 = L1; E2 = L2e2t; E3 = L3e2t записать его в эйлеровых координатах.
Г.Для закона движения в п. В определить поля перемещений и скоростей в лагранжевых координатах.
135

1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД
Д.По найденному в п. Г полю скоростей определить поле тензора скоростей деформаций.
Е.Используя результаты пунктов В...Д, определить, куда переместится центр элементарного куба, первоначально (t = 0) находившегося в точке М(1, 1, 1), к моменту времени t = 1. Охарактеризовать и изобразить характер изменения во времени размеров, формы и объема куба.
Вариант 3 А. Каков физический смысл боковых компонент тензоров конечных дефор-
маций О. Коши и Л. Эйлера?
Б. Как вычисляется интенсивность сдвиговых деформаций?
В. По заданному закону движения в лагранжевых координатах E1 = L1e2t; E2 = L2; E3 = L3e–2t записать его в эйлеровых координатах.
Г.Для закона движения в п. В определить поля перемещений и скоростей в лагранжевых координатах.
Д.По найденному в п. Г полю скоростей определить поле тензора скоростей деформаций.
Е.Используя результаты пунктов В...Д, определить, куда переместится центр элементарного куба, первоначально (t = 0) находившегося в точке М(1, 1, 2), к моменту времени t = 1. Охарактеризовать и изобразить характер изменения во времени размеров, формы и объема куба.
Вариант 4 А. Во что преобразуется поверхность элементарного шара в общем случае его
деформирования?
Б. Как вычисляются главные деформации?
В.По заданному закону движения в лагранжевых координатах E1 = L1e2t; E2 = L2e–2t; E3 = L3 записать его в эйлеровых координатах.
Г.Для закона движения в п. В определить поля перемещений и скоростей в лагранжевых координатах.
Д. По найденному в п. Г полю скоростей определить поле тензора скоростей деформаций.
Е. Используя результаты пунктов В...Д, определить, куда переместится центр элементарного куба, первоначально (t = 0) находившегося в точке М(1, 3, 2), к моменту времени t = 1. Охарактеризовать и изобразить характер изменения во времени размеров, формы и объема куба.
Вариант 5 А. Каков физический смысл сферической части тензора малых деформаций?
Б. Запишите условие несжимаемости сплошной среды.
136

1.2. КИНЕМАТИКА
В.По заданному закону движения в лагранжевых координатах E1 = L1; E2 = L2e–2t; E3 = L3e2t записать его в эйлеровых координатах.
Г.Для закона движения в п. В определить поля перемещений и скоростей в лагранжевых координатах.
Д.По найденному в п. Г полю скоростей определить поле тензора скоростей деформаций.
Е.Используя результаты пунктов В...Д, определить, куда переместится центр элементарного куба, первоначально (t = 0) находившегося в точке М(1, 2, 2), к моменту времени t = 1. Охарактеризовать и изобразить характер изменения во времени размеров, формы и объема куба.
Вариант 6
А.Почему полная и частная производные тензорного поля по времени в лагранжевых координатах совпадают?
Б.Каков физический смысл боковых компонент тензоров конечных деформаций Г. Грина и Ж. Лагранжа?
В. По заданному закону движения в лагранжевых координатах E1 = L1e–2t; E2 = L2e2t; E3 = L3 записать его в эйлеровых координатах.
Г.Для закона движения в п. В определить поля перемещений и скоростей в лагранжевых координатах.
Д. По найденному в п. Г полю скоростей определить поле тензора скоростей деформаций.
Е.Используя результаты пунктов В...Д, определить, куда переместится центр элементарного куба, первоначально (t = 0) находившегося в точке М(1, 1, 0), к моменту времени t = 1. Охарактеризовать и изобразить характер изменения во времени размеров, формы и объема куба.
Вариант 7 А. На какие простейшие составляющие можно разложить всякое механичес-
кое движение?
Б. Почему вычисление вектора скорости по компонентам вектора перемещения и по пространственным координатам дает одинаковый результат?
В. По заданному закону движения в лагранжевых координатах E1 = L1e–3t; E2 = L2e3t; E3 = L3 записать его в эйлеровых координатах.
Г. Для закона движения в п. В определить поля перемещений и скоростей в лагранжевых координатах.
Д. По найденному в п. Г полю скоростей определить поле тензора скоростей деформаций.
137

1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД
Е. Используя результаты пунктов В...Д, определить, куда переместится центр элементарного куба, первоначально (t = 0) находившегося в точке М(2, 1, 1), к моменту времени t = 1. Охарактеризовать и изобразить характер изменения во времени размеров, формы и объема куба.
Вариант 8 А. Каков физический смысл девиатора деформаций?
Б. Каков физический смысл эйлеровых координат?
В. По заданному закону движения в лагранжевых координатах E1 = L1e3t; E2 = L2; E3 = L3e–3t записать его в эйлеровых координатах.
Г.Для закона движения в п. В определить поля перемещений и скоростей в лагранжевых координатах.
Д. По найденному в п. Г полю скоростей определить поле тензора скоростей деформаций.
Е. Используя результаты пунктов В...Д, определить, куда переместится центр элементарного куба, первоначально (t = 0) находившегося в точке М(1, 1, 1), к моменту времени t = 1. Охарактеризовать и изобразить характер изменения во времени размеров, формы и объема куба.
Вариант 9 А. Каков физический смысл антисимметричной части тензора дисторции?
Б. Как вычисляется коэффициент изменения длины в лагранжевых координатах?
В. По заданному закону движения в лагранжевых координатах E1 = L1e–3t; E2 = L2e3t; E3 = L3 записать его в эйлеровых координатах.
Г. Для закона движения в п. В определить поля перемещений и скоростей в лагранжевых координатах.
Д.По найденному в п. Г полю скоростей определить поле тензора скоростей деформаций.
Е. Используя результаты пунктов В...Д, определить, куда переместится центр элементарного куба, первоначально (t = 0) находившегося в точке М(1, 2, 1), к моменту времени t = 1. Охарактеризовать и изобразить характер изменения во времени размеров, формы и объема куба.
Вариант 10
А.Как вычисляется коэффициент изменения длины в эйлеровых координатах?
Б. Чем характеризуется поступательное движение малой окрестности материальной частицы?
138

1.2. КИНЕМАТИКА
В.По заданному закону движения в эйлеровых координатах L1 = E1; L2 = E2et; L3 = E3e–t записать его в лагранжевых координатах.
Г. Для закона движения в п. В определить поля перемещений и скоростей в лагранжевых координатах.
Д. По найденному в п. Г полю скоростей определить поле тензора скоростей деформаций.
Е.Используя результаты пунктов В...Д, определить, куда переместится центр элементарного куба, первоначально (t = 0) находившегося в точке М(1, 2, 1), к моменту времени t = 1. Охарактеризовать и изобразить характер изменения во времени размеров, формы и объема куба.
Вариант 11
А.Каким тензором характеризуется жесткий поворот малой окрестности материальной частицы? Как вычислить этот тензор через перемещение?
Б. Как должен выглядеть тензор малых деформаций в малой окрестности материальной частицы, если в назначенных координатах наблюдаются только сдвиги?
В.По заданному закону движения в эйлеровых координатах L1 = E1et; L2 = E2e–t; L3 = E3 записать его в лагранжевых координатах.
Г.Для закона движения в п. В определить поля перемещений и скоростей в лагранжевых координатах.
Д. По найденному в п. Г полю скоростей определить поле тензора скоростей деформаций.
Е. Используя результаты пунктов В...Д, определить, куда переместится центр элементарного куба, первоначально (t = 0) находившегося в точке М(2, 2, 2), к моменту времени t = 1. Охарактеризовать и изобразить характер изменения во времени размеров, формы и объема куба.
Вариант 12
А.Чему равен в произвольный момент времени косинус угла между направленными волокнами dLk и dLj, первоначально параллельными осям Lk и
Lj?
Б. Как вычисляется тензор дисторции? Что он характеризует?
В.По заданному закону движения в эйлеровых координатах L1 = E1; L2 = E2e–2t; L3 = E3e2t записать его в лагранжевых координатах.
Г.Для закона движения в п. В определить поля перемещений и скоростей в лагранжевых координатах.
Д. По найденному в п. Г полю скоростей определить поле тензора скоростей деформаций.
139

1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД
Е. Используя результаты пунктов В...Д, определить, куда переместится центр элементарного куба, первоначально (t = 0) находившегося в точке М(1, 1, 1), к моменту времени t = 1. Охарактеризовать и изобразить характер изменения во времени размеров, формы и объема куба.
Вариант 13 А. Какие поля скоростей называются гармоническими?
Б. Как записываются конвективные слагаемые полной производной тензо-
n
ра Ta по времени t в эйлеровых координатах?
В. По заданному закону движения в эйлеровых координатах L1 = E1e–3t; L2 = E2e3t; L3 = E3 записать его в лагранжевых координатах.
Г. Для закона движения в п. В определить поля перемещений и скоростей в лагранжевых координатах.
Д. По найденному в п. Г полю скоростей определить поле тензора скоростей деформаций.
Е. Используя результаты пунктов В...Д, определить, куда переместится центр элементарного куба, первоначально (t = 0) находившегося в точке М(2, 1, 1), к моменту времени t = 1. Охарактеризовать и изобразить характер изменения во времени размеров, формы и объема куба.
Вариант 14 А. Как вычисляется средняя деформация?
Б. Что такое линия тока?
В. По заданному закону движения в эйлеровых координатах L1 = E1e3t; L2 = E2; L3 = E3e–3t записать его в лагранжевых координатах.
Г.Для закона движения в п. В определить поля перемещений и скоростей в лагранжевых координатах.
Д.По найденному в п. Г полю скоростей определить поле тензора скоростей деформаций.
Е.Используя результаты пунктов В...Д, определить, куда переместится центр элементарного куба, первоначально (t = 0) находившегося в точке М(1, 1, 1), к моменту времени t = 1. Охарактеризовать и изобразить характер изменения во времени размеров, формы и объема куба.
Вариант 15 А. Каков физический смысл диагональных компонент тензоров конечных
деформаций О. Коши и Л. Эйлера?
Б. Чему равно произведение якобианов JL и JE ?
140
