
книги / Математическое моделирование и основы научных исследований в сварке. Статистическая обработка и планирование эксперимента
.pdf
рез DX. Для дискретной и непрерывной случайной величины DX определяют соответственно по следующим формулам:
n |
b |
DX = ∑ P( X i ) (xi − MX )2 , DX= |
∫ x2 ϕ (x)dx − (MX )2 . |
i=1 |
a |
Величина рассеивания выборочных значений вокруг их среднего значения характеризуется эмпирической дисперсией S2:
|
|
1 |
|
N |
|
|
|
S 2 = |
|
∑ mi ( xi − xср )2 . |
|||
|
|
|
|
|||
|
|
N −1 i=1 |
|
|||
Для N ≥ |
25 |
|
|
|
|
|
|
|
|
1 |
|
N |
( xi − xср )2 . |
|
S 2 = |
∑ mi |
||||
|
N |
|||||
|
|
|
|
i=1 |
|
|
S 2 = S |
называется эмпирическим средним квадратическим откло- |
|||||
нением или стандартным отклонением случайной величины Х. При N → ∞
S2 = DX.
Свойства дисперсии:
−дисперсия постоянной равна нулю;
−для любой неслучайной постоянной а
D (X + a) = D (X), D (aX) = a2DX.
Кроме первого и второго моментов при описании случайных величин иногда используют и другие моменты: третий, четвертый и т.д. Наиболее распространенными являются третий и четвертый центральные моменты – соответственно асимметрия А и эксцесс Е:
|
∑ mi (xi − xср)3 |
|
∑ mi (xi − xср)4 |
|
|
A = |
i=1 |
, E = |
i=1 |
. |
|
S 3 |
S 4 |
||||
|
|
|
При нормальном распределении асимметрия равна нулю, а эксцесс – трем. Если А = 0, то кривая симметрична. Если А > 0, кривая имеет положительную асимметрию, а если А < 0 – отрицательную (рис. 3). Эксцесс характеризует крутизну кривой.
11
Стр. 11 |
ЭБ ПНИПУ (elib.pstu.ru) |
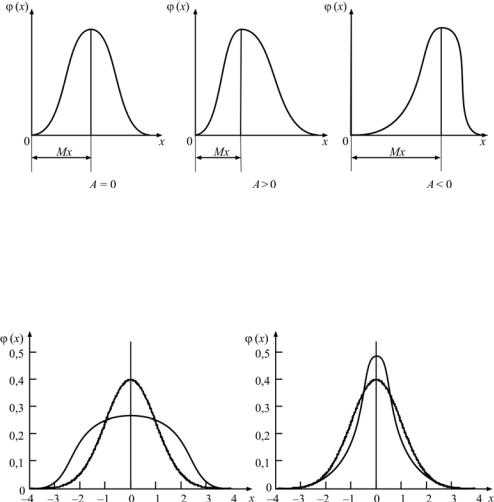
Рис. 3. Кривые распределения в зависимости от величины А
Если Е > 3, то говорят, что имеется положительный эксцесс, т.е. вершина кривой находится выше кривой нормального распределения; если Е < 3, имеется отрицательный эксцесс, и вершина кривой находится ниже кривой нормального распределения (рис. 4).
Рис. 4. Зависимость характера нормального распределения от E
Для случайных величин, принимающих вещественные значения, часто используют такие характеристики, как квантили. Квантилью хр случайной величины, имеющей функцию распределения F (x), называется решение хр уравнения F (x) = p. Величину хр часто называют р-квантилью или квантилью уровня р распределения F (x). Среди квантилей чаще всего используются медиана и квантили распределения.
Медианой называется квантиль, соответствующий значению р = 0,5. Верхним квантилем называется квантиль, соответствующий значению р = 0,75. Нижним квантилем называется квантиль, соответствующий зна-
чению р = 0,25.
12
Стр. 12 |
ЭБ ПНИПУ (elib.pstu.ru) |

При статистической обработке экспериментальных данных используются также такие величины, как коэффициент вариации Kv и размах R. Коэффициентом вариации называется отношение среднего квадратического отклонения к среднему значению случайной величины. Коэффициент вариации часто выражается в процентах, тогда полученное значение умножается на 100. Размахом R называется разность между крайними членами вариационного ряда. Размах, как и медиану, используют для характеристики выборок малого объема.
Для зависимых случайных величин часто необходимо оценить степень их зависимости друг от друга. Наиболее распространенными характеристиками являются ковариация и корреляция.
Ковариацию cov(Х, Y) случайных величин X и Y определяют по выражению
|
1 |
N |
|
cov ( X ,Y ) = M ( X − MX )(Y − MY ) = |
∑(xi − xср )( yi − yср), |
||
|
N i=1
если указанное математическое ожидание существует. Для независимых случайных величин ковариация равна нулю. Но равенство ковариации нулю не означает, что случайные величины независимы.
Использование ковариации в качестве меры связи случайных переменных неудобно, так как величина ковариации зависит от единиц измерения, в которых измерены случайные величины. При переходе к другим единицам (например, от метров к сантиметрам) ковариация также изменяется, хотя степень связи случайных величин остается прежней. Исходя из этого, для оценки связи случайных величин чаще используют характеристику, называемую коэффициентом корреляции. Коэффициент корреляции определяют по выражению
|
|
|
|
|
N |
|
|
|
cov( X ,Y ) |
|
|
∑(xi − xср )( yi − yср) |
|
||
corr( X , y) = |
= |
|
i=1 |
. |
|||
DX |
DY |
N |
N |
||||
|
|
|
|||||
|
|
∑(xi − xср)2 ∑( yi − yср )2 |
|
||||
|
|
|
|
|
|||
|
|
|
|
i=1 |
i=1 |
|
|
Если случайные величины X и Y линейно связаны, то коэффициент корреляции равен единице.
13
Стр. 13 |
ЭБ ПНИПУ (elib.pstu.ru) |
1.1.4. Техника вычисления параметров эмпирического распределения
Взависимости от объема выборки может быть рекомендована различная техника вычислений параметров выборки. Рассмотрим технику вычислений при объеме выборки N > 25, как наиболеечасто применяемом.
Вэтом случае все значения случайных величин целесообразно разбить на интервалы и произвести подсчет частот. Например, имеется 40 значений твердости (HRC) наплавленного металла от 26 до 40 единиц. Для вычислений составим таблицу (табл. 2), где через хi обозначены середины интервалов, в конце граф 3, 5 и 6 проставлены суммы соответствующих колонок.
|
|
|
|
|
Таблица 2 |
|
|
|
|
|
|
Номер |
Середина |
Частота |
xi2 |
mixi |
mixi2 |
интервала |
интервала xi |
mi |
|
|
|
1 |
27 |
2 |
729 |
54 |
1458 |
2 |
29 |
5 |
841 |
145 |
4205 |
3 |
31 |
9 |
961 |
279 |
8649 |
4 |
33 |
12 |
1089 |
396 |
13 068 |
5 |
35 |
8 |
1225 |
280 |
9800 |
6 |
37 |
3 |
1369 |
111 |
4107 |
7 |
39 |
1 |
1521 |
39 |
1521 |
|
|
40 |
– |
1304 |
42 808 |
В таблице
|
N = ∑mi = 40 , ∑ mi xi |
= 1304 , ∑ mi xi |
2 = 42 808 . |
|||||||||
Ограничимся вычислением хср и S: |
|
|
||||||||||
|
|
|
|
|
x = |
∑ mi xi |
= |
1304 |
= 32, 6 ; |
|
||
|
|
|
|
|
|
∑ mi |
|
|
|
|||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
ср |
|
|
40 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
S 2 = |
∑ mi xi |
2 |
− x2 |
= |
42 808 |
− (32, 6)2 = 1070, 2 −1062,8 = 7, 4 ; S = 2,72. |
||||||
∑ mi |
|
|
||||||||||
|
|
ср |
40 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
Зависимость частоты попадания элементов выборки от соответствующего интервала группировки (см. табл. 2), представленная в графической форме, называется гистограммой выборки.
14
Стр. 14 |
ЭБ ПНИПУ (elib.pstu.ru) |
1.1.5. Нормальное распределение
Наиболее общие закономерности для многих вероятностных распределений определяются так называемым нормальным распределением. Вероятностная кривая, соответствующая такому распределению (кривая Гаусса), имеет вид симметричного колокола, и описывается только двумя параметрами: характеристикой центра α (математическим ожиданием исследуемой случайной величины) и дисперсией σ 2.
Вероятности событий, связанные с появлением того или иного значения х, определяются соответствующей площадью под кривой Гаусса. Бесконечное число наборов параметров (α , σ 2), а следовательно, и вероятностных кривых можно объединить в одну кривую, если вместо величины х исследовать распределение некоторой безразмерной функции этой величины: u = (x – α )/σ .
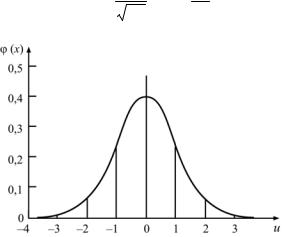
Величина u представляет собой отклонение величины х от ее математического ожидания, выраженное в долях стандартного отклонения σ . Преобразованное таким образом распределение называется нормальным нормированным распределением. Любому нормальному распределению с параметрами α и σ соответствует нормальное нормированное распределение с математическим ожиданием, равным нулю, и дисперсией, равной единице. Вероятностная кривая (рис. 5) нормированного распределения имеет вид
|
1 |
|
|
u |
2 |
|
ϕ (u) = |
|
− |
|
|
||
2π |
exp |
|
|
. |
||
|
|
|
2 |
|
||
Рис. 5. Вероятностная кривая нормированного нормального распределения
15
Стр. 15 |
ЭБ ПНИПУ (elib.pstu.ru) |

Нормирование позволяет создать единые таблицы для определения вероятностей попадания случайной величины в исследуемый интервал между −∞ и u1. Это определяется интегралом
Ф(u) = |
1 |
u1 |
|
− |
u |
2 |
|
|
exp |
|
du , |
||||
2π −∞∫ |
|
|
|||||
|
|
2 |
|
||||
что записывается в виде P (–∞ < u < u1). Определение вероятностей попадания случайной величины в заданный интервал можно оценить по рис. 6, на котором площади, описывающие соответствующие вероятности, заштрихованы. В то же время, поскольку вся площадь под нормированной кривой равна единице или (что одно и то же) 100 %, имеем
P (u2 < u < +∞ ) = 1 − Ф (u2).
Очевидно, что
P (u1 < u < u2) = Ф (u2) − Ф (u1).
1.1.6.Нормированная функция Лапласа
Для обработки экспериментальных данных интересен случай, когда величина х попадает в интервал между своим математическим ожиданием и некоторым значением х, а величина – в интервале между 0 и u1. Вероятность такого попадания
|
1 |
u1 |
|
|
u |
2 |
|
P(0 < u < u1) ) = |
∫0 |
exp |
− |
|
du = θ(u). |
||
2π |
|
|
|||||
|
|
2 |
|
||||
Функция θ (u) носит название нормированной функции Лапласа. Вероятность появления результатов, случайные отклонения которых находятся в симметричных граница х ± u, вычисляется на основании предыдущего случая (рис. 6):
P (–u1 < u < +u2) = 2θ (x).
Наконец, вероятность того, что случайная величина выходит за указанные в предыдущем случае симметричные границы, составит
P (u < −u1; u > u1) = 1 − 2θ (u1).
16
Стр. 16 |
ЭБ ПНИПУ (elib.pstu.ru) |
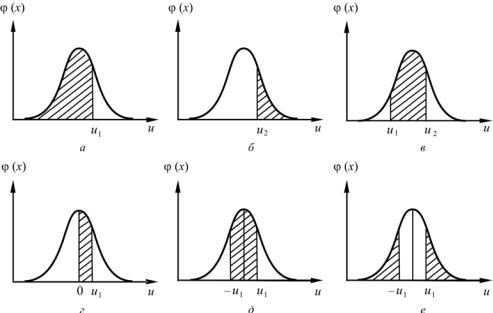
Рис. 6. Определение вероятностей |
попадания случайной величины |
в заданный интервал: а – P (−∞ |
< u < u1); б – P (u2 < u < ∞); |
в– P (u1 < u < u2); г – P (0 < u < u1); д – P (−u1 < u < u1); е – P (u < –u1; u < u1)
Спомощью таблиц можно вычислить вероятность результатов измерений, отклоняющихся от своего истинного значения не более чем
на ±σ , ±2σ и ±3σ . Этим значениям σ соответствуют значения u, равные
±1, ±2 и ±3.
Для u = 1; 2 и 3 по таблицам функции Лапласа находим соответствен-
ноθ (1) = 0,34; θ (2) = 0,477 иθ (3) = 0,4986. Наоснованииэтогополучим P (−1 < u < 1) = 2θ (1) = 2 0,34 = 0,68, или 68 %;
P (−2 < u < 2) = 2θ (2) = 2 0,477 = 0,954, или 95,4 %;
P (−3 < u < 3) = 2θ (3) = 2 0,4986 = 0,9972, или 99,72 %.
Таким образом, лишь в 68 % случаев результаты не выходят за пределы одной стандартной погрешности и лишь в 0,28 % случаев выходят за пределы ±3σ . Частота таких событий настолько мала, что результат с отклонением более ±3σ принято считать грубым промахом. Это правило выявления промахов называют критерием трех сигм.
Выводы относительно степени достоверности экспериментальных результатов корректны только в том случае, если они согласованы с вероятностью получения этих результатов. Результат тем достовернее, чем больше вероятность его получения. Для практических целей, т.е. для ре-
17
Стр. 17 |
ЭБ ПНИПУ (elib.pstu.ru) |

шения вопроса о необходимой степени достоверности, нужно лишь условиться о минимальном значении этой вероятности.
Практически для большинства естественно-научных экспериментов вероятность заслуживает доверия, если в 95 случаях из 100 наблюдаются допустимые случайные отклонения результатов от среднего. Таким образом, вероятности, значения которых лежат вблизи 0,95, носят название доверительных. Выражение результата измерения некоторой величины А в виде А± ε (где ε − погрешность эксперимента) без указания вероятности получения результата не дает никакой информации о егодостоверности.
1.1.7. Некоторые выборочные распределения, применяемые при статистических исследованиях
Многие случайные процессы близки по характеру теоретическому нормальному распределению. Большинство же реальных выборок следует этому распределению лишь при очень большом объеме выборки. Однако статистические исследования с помощью больших выборок и в практических, и в исследовательских задачах используются сравнительно редко, особенно если эксперименты трудоемки и дороги.
Каждая из выборочных статистик, в отличие от нормального распределения, зависит от числа степеней свободы. Этим термином обозначается число независимых способов описания исследуемой выборки. Так, если значение математического ожидания ξ заранее известно (например, если производят анализ стандартного образца с целью проверки правильности методики анализа), то число степеней свободы ƒ для n параллельных опытов будет равно n, т.е. общему объему выборки. Если же значение ξ оценивается на опыте как среднее арифметическое хс этих же n измерений, то число степеней свободы будет равно n – 1, так как из общего числа случайных величин вычитается дополнительная связь между всеми элементами выборки, затраченная при определении значения хс.
Дисперсия среднего σ 2 (xc ) зависит от объема n выборки следующим образом:
σ2 (xc )= σ 2 (x)/ n ,
откуда средняя квадратическая погрешность среднего
σ (xc )= σ (x)/  n .
n .
Из приведенного выражения следует, что в отсутствие систематических погрешностей средняя квадратическая погрешность измере-
18
Стр. 18 |
ЭБ ПНИПУ (elib.pstu.ru) |
ний может быть сделана сколь угодно малой, если увеличивать число параллельных опытов. Однако, как следует из приведенного выражения, для улучшения воспроизводимости на один порядок требуется произвести 100 измерений, что значительно увеличивает продолжительность и стоимость измерений. В то же время условие отсутствия систематических погрешностей фактически означает, что эти погрешности существенно меньше случайных. По мере уменьшения средней квадратической погрешности с увеличением n случайная погрешность уменьшается, и систематическая погрешность может стать больше случайной σ (xc ) . Таким образом, никакое дальнейшее увеличение чис-
ла параллельных измерений (опытов) не может уменьшить общую погрешность. Основным путем повышения точности измерения является применение или создание метода измерения с меньшим значением σ (xc ) , а не с увеличением n.
Распределение Стьюдента. Уменьшение объема выборки n при измерениях (n < 20…30) приводит к тому, что при одних и тех же значениях средних квадратических погрешностей и при одном и том же числе параллельных измерений (опытов) одному и тому же значению вероятности соответствуют значительно большие случайные отклонения от среднего, чем это следует из закона нормального распределения. Кроме того, если для нормального распределения значения таких отклонений не зависят от числа степеней свободы и определяются только доверительной вероятностью, то для выборочных распределений это число существенно влияет на случайное рассеяние результатов.
Если в выражении u = (x − ξ )/ σ вместо значения стандартной по-
грешности генеральной совокупности σ подставить значение выборочного стандартного отклонения S, мы получим величину
t = (x − ξ )/ S .
Распределение величины t следует особому закону, исследованному Стьюдентом (t-распределению). Вероятностная кривая этого распределения сходна по форме с кривой Гаусса, но более размыта вдоль оси абсцисс.
Распределение Пирсона χ 2 (хи-квадрат). Это распределение применяется для оценки погрешности определения дисперсии, для проверки принадлежности выборки к генеральной совокупности нор-
19
Стр. 19 |
ЭБ ПНИПУ (elib.pstu.ru) |
мального распределения, а также в качестве критерия однородности нескольких дисперсий.
Распределение отношений дисперсий. При сравнении методик измерения или данных по воспроизводимости двух экспериментов часто возникает необходимость оценки равенства генеральных дисперсий σ 12 и σ 22 на основании сведений о выборочных дисперсиях
S12 и S22 . Сравнение дисперсий производится на основании статистического критерия Фишера:
F = S12 / S22 ,
где S12 > S22 .
Величина F имеет несимметричное случайное распределение, которое, как χ 2-распределение, зависит исключительно от чисел степеней свободы f1 = n1 −1 и f 2 = n2 −1 обеих сравниваемых дисперсий.
Доверительная вероятность и доверительные границы. Каждо-
му значению доверительной вероятности соответствуют свои доверительные границы возможных отклонений результатов от среднего. Как уже было показано, для вероятности 0,95 (точнее 0,954) такие отклонения не превышают ±2σ. Для доверительной вероятности, в точности равной 0,95, эти отклонения не должны превышать ±1, 96σ.
Часто вместо доверительной вероятности Р используют величину
q = 1 − P,
которую называют уровнем значимости.
Доверительные границы математического ожидания результата для нормального нормированного распределения можно определить следующим образом.
Согласноранеерассмотреннойзамене(u = (x – ξ )/σ) можнозаписать
x – ξ |
= upσ ( x), |
отсюда получим ξ = xc ± upσ(x) / |
n . |
Поскольку известно, что дисперсия среднего σ 2 (хср) зависит от объема выборки следующим образом:
σ |
2 (x )= σ 2 |
(x) / n , |
|
c |
|
20 |
|
|
Стр. 20 |
ЭБ ПНИПУ (elib.pstu.ru) |
