книги / Физико-химические свойства взрывчатых веществ, порохов и твердых ракетных топлив

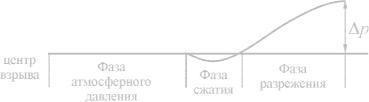
стью. Теплота, выделяющаяся при этой реакции, обусловливает поддержание энергии ударной волны, которая сжимает следующий слой ВВ и т.д.

Скорость распространения детонации по ВВ определяется скоростью ударной волны в данном веществе и составляет несколько километров в секунду. Скорость детонации в газах 1,5–3,5 км/с, а в конденсированных взрывчатых веществах достигает 8,5 км/с.

По мере распространения волны фронт обращается в «поверхность разрыва». На этой поверхности имеет место резкое скачкообразное изменение параметров состояния газа (давление, плотность, температура, скорость движения). Такую волну, характеризующуюся наличием поверхности разрыва основных физических параметров среды, называют ударной волной (рис. 11).

Рис. 11. Схема распространения ударной волны, вызванной взрывом в воздухе

Для количественной характеристики ударной волны надо определить следующие взаимосвязанные величины (параметры): скорость распространения ударной волны, скорость движения потока среды, давление, плотность и температуру возмущенной среды.

Рассмотрим (рис. 12) трубу с поперечным сечением 1 см2, заполненную покоящимся газом, давление которого р0 и плотность ρ0. Приводимые здесь соображения в принципе справедливы не только для газов, но и для конденсированных сплошных сред.

В трубу вдвигается поршень с постоянной скоростью u. Если бы в трубе находилось несжимаемое вещество, то внезап-

191

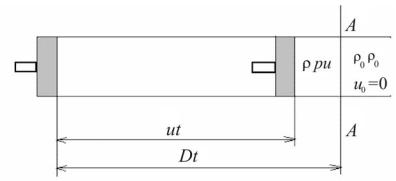
ное движение поршня мгновенно передалось бы всей массе вещества, заполняющей трубу. В сжимаемом же газе возмущение, вызванное движением поршня, передается с конечной скоростью, поэтому впереди поршня образуется конечная зона газа, сжатого до давления р и плотности ρ.

Рис. 12. Схема образования ударной волны в трубе движением поршня

При движении системы поршень – сжатый газ все новые массы невозмущенного газа сжимаются до давления р и плотности ρ и приобретают скорость и, вследствие чего зона сжатого газа непрерывно увеличивается. Граница этой зоны (плоскость АА на рис. 12) перемещается вдоль трубы с некоторой скоростью D. Справа от АА – неподвижный газ с начальными параметрами (давление р0, плотность ρ0, температура Т0), слева – газ, сжатый до давления р с плотностью ρ и двигающийся со скоростью поршня и. На границе раздела (фактически представляющей собой не плоскость, но некоторую область конечной, хотя и весьма малой ширины), называемой фронтом ударной волны, значения параметров, характеризующих состояние газа, изменяются очень резко, скачкообразно.

Если сжатие газа происходит настолько быстро, что можно пренебречь потерями энергии за счет теплопроводности, и если не учитывать внутреннее трение в газе и трение

192

между движущимся газом и поверхностью трубы, то легко получить уравнения, связывающие параметры ударной волны. Для этой цели используем основные законы механики и термодинамики:

1) уравнение сохранения массы (уравнение неразрывно-

сти);

2)уравнение сохранения импульсов;

3)уравнение сохранения энергии;

4)уравнение состояния газа.

Уравнение сохранения массы. За время t граница АА

(см. рис. 11) уйдет от начального положения поршня на расстояние Dt. Масса вещества, которая подверглась сжатию за это время, равна ρ0Dt. Она равна массе газа, сжатого до плотности ρ между поршнем, продвинувшимся на расстояние ut, и плоско-

стью АА – ρ(D–u)t.

По закону сохранения массы запишем ρ0Dt = ρ(D–u)t, или

Уравнение сохранения импульсов. Указанная масса вещест-

ва приобрела скорость, равную скорости движения поршня и. Импульс, приобретенный массой газа, заключенной между поршнем и фронтом волны, за время t, равен ρ0Dtu. Этот импульс равен импульсу сил давления за это же время (р–p0)t. Поэтому ρ0Dtu = (р–p0)t, или

Уравнение сохранения энергии. Приращение энергии веще-

ства при сжатии равно работе внешней силы, перемещающей поршень за время t.

При давлении р на поршень, прошедший путь ut, работа внешней силы равна put. Приращение энергии для единицы массы газа равно

E − E0 + u22 ,

193

где E – E0 – приращение внутренней энергии; u2 – приращение

2

кинетической энергии единицы массы вещества.

Для массы газа ρ0Dt, подвергшейся сжатию, приращение энергии составит

3.6.1. Общие соотношения для ударных волн. Адиабата Гюгонио

Преобразуем полученные уравнения. Уравнение (1) можно представить в виде

Так как при сжатии газа ρ > ρ0 , то из (4) непосредственно

следует, что D и и направлены в одну сторону, причем D > u. Из уравнений (1) и (2) определим D и и:

Подставляя (5) и (6) в (3), после простых преобразований получим

Этому уравнению, показывающему, какие состояния могут получиться из данного начального состояния (ρ0, V0) путем однократного сжатия при переходе через фронт ударной волны, соответствует в плоскости (р, V) кривая, называемая адиабатой Гюгонио.

Адиабата Гюгонио для идеального газа. Считая, что для вещества, сжатого в волне, справедливо уравнение состояния идеального газа, можно записать

Как известно, для идеального газа с постоянной теплоемкостью сV

Подставляя значения Е – Е0 из уравнения (9) в уравнение (7), получим

Это уравнение адиабаты Гюгонио для идеального газа. Уравнение (10) связывает значения плотности и давления

перед фронтом и позади фронта и характеризует процесс сжатия в ударной волне. В предельном случае, когда p > p0, из уравнения (10) получим

Таким образом, даже при неограниченном росте давления в ударной волне плотность газа сохраняет конечное значение.

Это обстоятельство существенно отличает ударное сжатие от обратимого сжатия, например, по закону изэнтропы (адиабаты Пуассона).

Непосредственно из уравнения (10) можно видеть, что сжатие в ударной волне является необратимым. Так, если из одного и того же начального состояния (р0, ρ0) газ сжимается

вударной волне в одном случае сразу до давления р1, а в другом сначала до некоторого давления р' (р < р' < р1), а затем второй ударной волной до того же давления р1, то конечные состояния сжатого газа будут различны.

Существенно, что необратимый характер процесса сжатия

вударной волне обусловлен не внешними потерями (теплопроводность, трение), которые не были учтены в предыдущих выводах, а присущ самому явлению. В связи с этим интенсивность ударной волны, распространяющейся в инертной среде, падает по мере удаления от источника, вызвавшего волну.

Из уравнений (5), (6) и (10) можно, задаваясь одним из па-

раметров волны, например, отношением давлений p , опреде-

Если ударная волна распространяется в какой-либо газообразной среде, и в частности в воздухе, то последнюю можно принять за идеальный газ и применить в качестве четвертого уравнения уравнение состояния идеального газа

где п – число грамм-молей в единице массы или веса газа.

С помощью последнего уравнения, принимая во внимание, что для идеального газа имеет место равенство

∆E = сv ∆T ,

формула(7) может быть преобразована следующим образом:

Удельная же теплоемкость идеального газа при постоянном объеме равняется

где k – отношение теплоемкостей сp/сV.

Поэтому уравнение (13) можно переписать в таком виде:

197

или же на основании уравнения (12)

Таким образом, для вычисления неизвестных величин при решении задач, связанных с распространением ударных волн в идеальном газе, имеется система четырех уравнений: (5); (6); (12) и (15).

Неизвестными величинами в этих уравнениях являются: D, W, p, V, T, а остальные – заданными.

Задав какую-либо из неизвестных величин, можно с помощью вышеуказанной системы уравнений найти все остальные.

При решении практических задач заданной величиной обычно является величина скорости волны D, да к тому же эта величина сравнительно просто может быть измерена опытным путем.

Но можно, задав, например, величину давления, определить наряду с другими параметрами величину скорости волны D. Здесь необходимо отметить, что давление во фронте детонационной волны не следует смешивать с рассмотренным нами ранее давлением, развивающимся при взрыве заряда ВВ в замкнутом объеме, которое может быть вычислено с помощью урав-

взрыва. Это последнее является средним давлением, развивающимся в замкнутом объеме в результате взрыва всего заряда ВВ, а поэтому оно значительно меньше давления во фронте детонационной волны.

То же самое следует сказать о температуре и других параметрах детонационной волны.

Согласно гидродинамической теории детонации, предполагается, что при детонации взрывчатого вещества по его заряду пробегает ударная волна, во фронте которой протекает реакция взрывчатого превращения ВВ.

198

3.6.2. Детонация газов

Движение обычной ударной волны складывается из движения скачка уплотнения и перемещения самой среды. Детонационная волна обладает более сложной структурой; распространение последней обусловливается движением ударной волны, зоны химической реакции и конечных продуктов взрыва.

Разница между ударной и детонационной волнами заключается в том, что первая, т.е. ударная волна, распространяется в инертной среде и вследствие необратимых потерь кинетической энергии быстро затухает и вырождается в обычную звуковую волну.

Вторая же, т.е. детонационная волна, представляет собою ударную волну, распространяющуюся по заряду взрывчатого вещества; потери ее энергии компенсируются за счет теплоты, выделяющейся при химической реакции, протекающей в зоне, охваченной волной, благодаря чему она может распространяться с постоянной скоростью, характерной для данного ВВ и данных условий опыта.

Для описания стационарного процесса детонации достаточно сопоставить состояние исходного вещества и конечных продуктов реакции. Сама зона реакции может не рассматриваться. При этом для определения параметров детонационных волн мы можем воспользоваться основными уравнениями теории ударных волн.

Приведенные выше уравнения для ударной волны применимы и для детонационной волны; необходимо только в уравнениях, выражающих закон сохранения энергии (7) или для случая газовой детонации (15), учесть теплоту взрыва QV.

После учета теплоты взрыва уравнения (7) и (15) будут иметь соответственно следующий вид:

Уравнения же (5) и (6), являющиеся следствием законов сохранения массы и импульса, остаются без изменения.

На основании сказанного для решения задач, связанных с вычислением параметров детонационной волны в случае газовой детонации, могут быть применены уравнения (5), (6), (12) и (17).

Так как неизвестных в этих уравнениях пять, а именно: D, W, p, V и T, то для однозначного решения задачи определения параметров детонационной волны необходимо еще одно уравнение. В качестве такого недостающего уравнения применяется так называемое уравнение Жуге, которое имеет следующий вид:

Это уравнение может быть выведено из того положения, что скорость детонационной волны равняется скорости потока продуктов детонации за фронтом волны плюс скорость звука в этих продуктах, т. е. на основании уравнения

где c – скорость звука в продуктах детонации.

Таким образом, для вычисления параметров детонационной волны и в том числе скорости детонации D в случае газовой детонации имеется система из следующих пяти уравнений:

200