книги / Сборник задач по общей физике

Глава 3. ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ

3.1. Электростатика

Задачи по электростатике удобно разделить на три группы. К первой можно отнести задачи о точечных зарядах и системах, сводящихся к ним, ко второй – все задачи о заряженных телах, размерами которых нельзя пренебречь, к третьей – задачи на определение емкости, потенциала или заряда какого-либо тела, расчет соединений конденсаторов и энергии электрического поля.

Решение задач первой группы основано на применении законов механики совместно с законом Кулона и вытекающих из него следствий. Такие задачи рекомендуется решать в следующем порядке:

1.Расставить силы, действующие на точечный заряд, помещенный в электрическое поле, записать для него уравнение равновесия или уравнение второго закона Ньютона.

2.Выразить силы электрического взаимодействия через заряды и характеристики поля и подставить эти выражения в исходное уравнение. Силы взаимодействия зарядов можно рассчитать или

, считая, что один из за-

рядов находится в поле действия другого.

3.Если при взаимодействии заряженных тел между ними происходит перераспределение зарядов, к составленным уравнениям добавляют уравнение закона сохранения зарядов.

4.Далее записывают вспомогательные формулы и решают систему уравнений относительно неизвестной величины.

9 109 м/Ф. Именно такое значение и следует подставлять в окончательную формулу.

71

Во вторую группу входят задачи, связанные с расчетами напряженности и потенциала электрического поля, создаваемого системами точечных зарядов, заряженными плоскостями и телами сферической формы.

В задачах на вычисление напряженности электрического поля особое внимание нужно обратить на векторный характер Е:

–векторы напряженности электрического поля уединенного точечного заряда направлены от заряда, если он положителен, и к заряду, если он отрицателен;

–поле заряженной плоскости однородно; векторы напряженности поля плоскости направлены перпендикулярно ее поверхности от плоскости, если ее заряд положителен, и к плоскости, если заряд отрицателен;

–для электрического поля заряженной сферы в точках, расположенных за ее пределами, векторы напряженности направлены так же, как у точечного заряда, находящегося в центре сферы; внутри сферы электрическое поле равно нулю;

–для поля шара, заряженного равномерно по объему, в точках, расположенных за его пределами, векторы напряженности направлены так же, как у сферы; внутри – как у точечного заряда, помещенного в центр шара (совпадают только направления, а не величины!); если шар проводящий, то нескомпенсированные заряды расположатся на его поверхности, что с точки зрения электростатики эквивалентно заряженной сфере;

–электрическое поле внутри проводника и внутри полой проводящей оболочки отсутствует (это справедливо независимо от наличия у проводника заряда и внешнего электрического поля).

При решении задач данной группы часто используется метод дифференцирования и интегрирования (метод ДИ).

Сущность метода ДИ заключается в следующем. Предположим, что физический закон имеет вид K = LM, где K, L, М – некоторые физические величины. Выделим столь малый промежуток dМ изменения величины М, чтобы изменением величины на этом промежутке можно было пренебречь (рисунок). Таким образом,

72

приближенно на участке dМ можно L считать постоянной

(L = const).

Тогда

dK = L(M)dM,

где dK – изменение величины K на участке dM.

Используя принцип суперпозиции (суммируя величины по всем участкам изменения величины М), получаем значение

M2

величины K в виде K L M dM , где М1 и М2 – начальное

M1

и конечное значения величины М. Таким образом, метод ДИ состоит из двух частей. В первой находят дифференциал искомой величины. Для этого в большинстве случаев производят или деление тел на столь малые части, чтобы последние можно было принять за материальные точки, или деление большого промежутка времени на такие малые промежутки времени dt, чтобы в течение этих малых промежутков процесс можно было п р и б л и - ж е н н о считать равномерным (или стационарным), и т.д.

Во второй части метода производят суммирование (ин-

тегрирование). Наиболее трудными в этой части являются выбор переменной интегрирования и определение пределов интегрирова-

ния. Для определения переменной интегрирования необходимо детально проанализировать, от каких переменных зависит дифференциал искомой величины и какая переменная является главной, наиболее существенной. Эту переменную чаще всего и выбирают в качестве переменной при интегрировании. После этого все остальные переменные выражают как функции от этой переменной. В результате дифференциал искомой величины принимает вид функции от переменной интегрирования. Затем определяют пределы интегрирования как крайние (предельные) значения пере-

73

менной интегрирования. После вычисления определенного интеграла получают числовое значение искомой величины.

Третью группу составляют задачи на определение емкости, потенциала или заряда какого-либо тела, расчет соединений конденсаторов и энергии электрического поля.

Если по условию задачи дано одно заряженное тело, то величины, характеризующие электрические свойства тела, связаны между собой известными формулами

С учетом зависимости потенциала от величины заряда эти формулы позволят найти одни из величин, если другие заданы.

Следует иметь в виду, что если плоский конденсатор подключить к источнику питания, зарядить его и затем отключить, то при изменении емкости конденсатора С вследствие раздвижения (сближения) пластин, внесения (удаления) диэлектрика заряд на конденсаторе не меняется. Что при этом происходит с напряжением U или энергией конденсатора W, легко установить, анализируя вышеприведенные формулы. Если же конденсатор подключен к источнику постоянного напряжения, то при всех изменениях емкости конденсатора напряжение между его пластинами остается неизменным.

Основные формулы

1. Закон Кулона

вектор, направленный от q1 к q2; r – модуль r12 ; ε – диэлектриче-

ская проницаемость среды, ε EE0 ; Е0 – напряженность электро-

74

статического поля в вакууме; Е – напряженность электростатического поля внутри однородного диэлектрика; 0 – электрическая постоянная.

2. Напряженность электрического поля и потенциал

где Wп – потенциальная энергия положительного точечного заряда q, находящегося в данной точке поля.

Сила, действующая на точечный заряд q, находящийся в электрическом поле, и потенциальная энергия этого заряда

FqE, Wп = q .

3.Напряженность и потенциал поля, создаваемого точечным зарядом q,

где r – расстояние от заряда q до точки, в которой определяются напряженность или потенциал.

4. Напряженность и потенциал поля, создаваемого системой точечных зарядов (принцип суперпозиции полей),

75

где q – заряд сферы.

6. Линейная плотность заряда τ dqdl , или = q/l. Поверхностная плотность заряда σ dq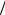dS , или = q/S. Объемная плотность заряда ρэ dq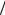dV , или э = q/V.

Связь заряда и плотностей dq = dS = dl = эdV.

7. Напряженность и потенциал поля, создаваемого распределенными зарядами. Если заряд равномерно распределен вдоль линии с линейной плотностью , то на линии выделяется малый участок длиной dl с зарядом dq = dl. Такой заряд можно рассматривать как точечный и применять формулы

Интегрирование ведется вдоль всей длины l заряженной ли-

нии.

8. Напряженность поля, создаваемого бесконечно прямой равномерно заряженной линией или бесконечно длинным цилиндром,

E 2πεετ 0r ,

где r – расстояние от нити или оси цилиндра до точки, в которой определяется напряженность поля.

76

Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью,

в) E ddr в случае поля, обладающего центральной или

осевой симметрией.

10. Электрический момент диполя

P q l ,

где q – заряд; l – плечо диполя (векторная величина, направленная от отрицательного заряда к положительному и численно равная расстоянию между зарядами).

11.Работа сил поля по перемещению заряда q из точки поля

спотенциалом 1 в точку с потенциалом 2

2

A12 q El dl q 1 2 .

1

77

12. Электроемкость уединенного тела и конденсатора

С = q , С = Uq ,

где – потенциал проводника; U – разность потенциалов пластин конденсатора.

Следует помнить, что при изменении электрической емкости конденсатора, подключенного к источнику напряжения, меняется величина заряда на его пластинах, а разность потенциалов остается постоянной и равной ЭДС источника тока. При изменении емкости конденсатора, отключенного от источника напряжения, меняется разность потенциалов на его пластинах, а величина заряда остается при этом неизменной.

Электроемкость плоского конденсатора

C = εεd0 S ,

где S – площадь одной пластины конденсатора; d – расстояние между пластинами.

Электроемкость батареи конденсаторов:

i 1

где N – число конденсаторов в батарее. Энергия заряженного конденсатора

W 12 ε0ε E2V ,

где V – объем конденсатора.

Объемная плотность энергии электрического поля

wэ W ε0ε E2 .

V 2

78

Примеры решения задач

№1. Три точечных заряда q1 = q2 = q3 = 1 нКл расположены

ввершинах равностороннего треугольника. Какой заряд q4 нужно поместить в центре треугольника, чтобы указанная система зарядов находилась в равновесии?

Р е ш е н и е.

Все три заряда, расположенные по вершинам треугольника, находятся в одинаковых условиях, поэтому достаточно выяснить, какой заряд следует поместить в центре треугольника, чтобы ка-

кой-нибудь один из трех зарядов, например q1, находился в равновесии. Заряд q1 будет находиться в равновесии, если векторная сумма действующих на него сил равна нулю:

Поскольку силы F и F4 направлены по одной прямой

в противоположные стороны, то векторное равенство (1) можно заменить скалярным равенством F – F4 = 0, откуда

F4 = F.

79

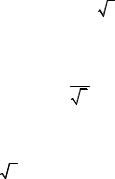
Выразив в последнем равенстве F через F2 и F3 и учитывая,

С учетом этого формула (2) примет вид

q4 q13 .

Подставив числовое значение q1 = 1 нКл = 10–9 Кл, получим

q4 10 9 5,77 10 10 577 пКл. 3

Следует отметить, что равновесие системы зарядов будет неустойчивым.

№ 2. Тонкий стержень длиной l = 20 см несет равномерно распределенный заряд. На продолжении оси стержня на расстоянии а = 10 см от ближайшего конца находится точечный заряд q1 = 40 нКл, который взаимодействует со стержнем с силой F = 6 мкН. Определить линейную плотность τ заряда на стержне.

80