
книги / Основы теории цепей. Ч. 2
.pdf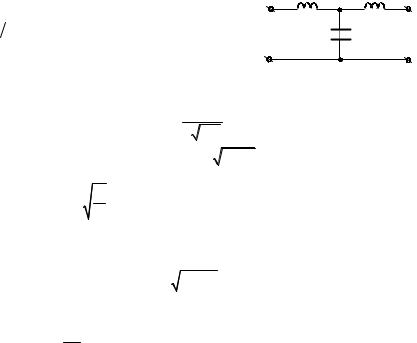
Найти: параметры L, |
C фильтра; |
L/2 |
L/2 |
|||||
коэффициент затухания Α и величину |
|
|
||||||
U1 U2 на частоте ω1 . |
|
|
|
|
|
C |
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L, C определим при |
помощи сле- |
Рис. 3.15 |
|
|||||
дующих формул: |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
1 |
|
|
|
|
|
ω0 = |
, |
|
|
|
|
||
|
|
|
2 |
LC |
|
|
|
|
|
|
|
= − jρ ν |
2 |
−1, |
|
|
|
|
Z CТ |
|
|
|
||||
где ν = ω0 , ρ = |
L . |
|
|
|
|
|
|
|
ω |
C |
|
|
|
|
|
|
|
В результате получаем L = 16 мГн, C = 25 нФ. |
|
|||||||
Коэффициент затухания |
|
|
|
|
|
|
||
|
Α = ln(−A |
+ |
A2 |
−1) = ln 4 =1,3863 , |
|
|||
|
11 |
|
11 |
|
|
|
|
|
где A11 =1 − 2ν2 =1 − 2 1, 252 = −2,125 .
Тогда U1 = 4 .
U2
Вопросы и упражнения для самоконтроля
1.Какие значения принимают коэффициент затухания и модуль передаточной функции по напряжению идеального фильтра в полосе:
а) пропускания; б) затухания?
2.Почему при каскадном соединении звенья многозвенных фильтров должны быть характеристически согласованы?
3.Изобразите зависимость коэффициента затухания Α(ω) иде-
ального фильтра:
а) нижних частот; б) верхних частот; в) полосового;
131
г) заграждающего от частоты.
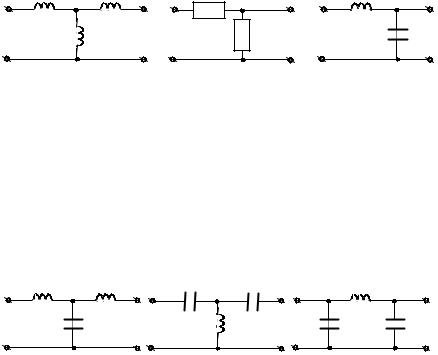
4. Обладают ли фильтрирующими свойствами электрические цепи, изображенные на рис. 3.16?
L1 |
L2 |
R1 |
L |
|
L3 |
R2 |
C |
|
а |
б |
в |
|
|
Рис. 3.16 |
|
5. Определить, какой полосе частот принадлежит рабочая частота фильтров (рис. 3.17), если:
а) X L |
= X L |
|
= |
Z1 |
|
=1 Ом, X C = Z 2 =8 Ом; |
|
|
|
|
|||||
1 |
2 |
2 |
|
|
|||
|
|
|
|
|
|||
б) X C |
= X C |
|
= |
Z1 |
=8 Ом, X L = Z 2 = 0,5 Ом; |
||
|
|
||||||
1 |
|
2 |
2 |
|
|
||
|
|
|
|
|
|
||
в) X C1 |
= X C2 |
= 2Z 2 = 2 Ом, X L = Z1 = 4 Ом. |
|||||
X L |
|
X L |
X C1 |
X C2 |
XL |
|
|
1 |
|
2 |
|
|
|
|
|
|
X |
C |
XL |
|
X C |
X C |
2 |
|
|
|
|
1 |
|
||
|
а |
|
б |
|
в |
|
|
|
|
|
Рис. 3.17 |
|
|
|
|
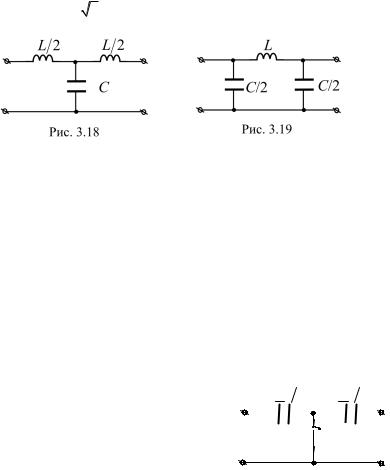
6. Для фильтра низких частот (рис. 3.18) заданы коэффициент фильтра k =12,5 и частота среза ωc = 2,5 105 с-1. Определить характеристическое сопротивление на частоте ω=10 с-1.
7. Дан |
фильтр высоких частот, частота среза которого |
ωc = 25 103 |
с-1 и характеристическое сопротивление Z C = − j600 Ом |
при ω1 = 20 103 с-1. Определить коэффициент затухания.
132
8. Из двух конденсаторов емкостью 4нФ и индуктивности 0,34 мГн собран низкочастотный фильтр. Какова полоса пропуска-
ния такого фильтра? |
|
9. Дан Т-фильтр высоких частот (рис. 3.19), |
у которого |
С1 = С2 = 0,16 мкФ, L = 0,02 Гн. Определить на частоте f |
= 3 кГц мгно- |
венное значение напряжения на выходе фильтра при согласованной нагрузке, если U&1 = 50 2 В.
10. Из двух индуктивностей величиной 0,05 Гн и емкости 0,1 Ф собран фильтр высоких частот. Определить коэффициент фильтра и мгновенное значение выходного напряжения в согласованном режиме на частоте ω1 =104 с-1, если U&1 =10 В.
11.Подобрать индуктивность L фильтра (см. рис. 3.11) так, чтобы частота среза fc =10 кГц, емкость С = 0,1 мкФ.
12.Определить полосу пропускания и характеристическое сопротивление фильтра (см. рис. 3.19) при L = 10 мГн, С = 0,8 мкФ.
13.Т-образный фильтр верхних частот типа k состоит из двух
конденсаторов емкостью 2С1 = 0,16 мкФ каждый и катушки с индуктивностью L2 = 0,02 Гн (рис. 3.20). Построить графики зависимости коэффициента затухания Α , коэффициента фазы Β и характеристиче-
ского сопротивления Z CТ от частоты. При входном напряжении U1 =100 В и частоте f = 3 кГц вычислить комплексные значе-
ния всех токов и напряжений в схеме фильтра и построить векторную диаграмму токов и напряжений.
Z1 2 |
Z1 2 |
|
|
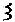 Z 2
Z 2
Рис. 3.20
133
4. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
4.1. ОБЩИЕ ВОПРОСЫ ТЕОРИИ ПЕРЕХОДНЫХ ПРОЦЕССОВ
Говоря о работе электрической цепи, следует различать установившиеся или стационарные режимы и переходные или динамические режимы.
Установившееся или стационарное состояние электрической цепи характеризуется вполне определённой картиной распределения токов, напряжений и электромагнитной энергии между элементами. Это распределение оказывается либо неизменным во времени, если в цепи действуют источники постоянных воздействий, либо периодически меняющимся, как это имеет место при гармонических или негармонических периодических воздействиях.
Стационарные режимы в электрических цепях могут нарушаться в результате действия так называемых возмущений, которые делятся на параметрические (изменение параметров элементов цепи вследствие каких-либо внешних или внутренних причин) и коммутационные (присоединение или отключение некоторых элементов цепи или её частей). Происходящие при этом изменения структуры цепи называют коммутацией.
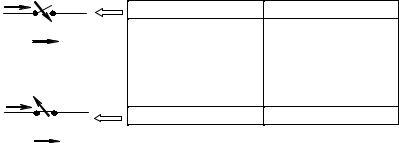
Любое возмущение эквивалентируется в расчетных моделях идеализированным элементом – коммутатором, который может замыкать или размыкать контакты 1 и 2 (рис. 4.1), изменяя режим работы цепи.
Изменение состояния коммутатора происходит в течение времени ∆t . Идеализация заключается в устремлении промежутка ∆t → 0 . Именно этот момент времени соответствует началу переходного процесса (t = 0) .
В результате коммутации образуется новая цепь, которую по истечении некоторого промежутка времени можно будет рассматривать
134
а) |
iк |
|
до коммутации |
после коммутации |
|
1 |
2 |
||
|
|
|
||
|
uк |
|
Rк = ∞ |
Rк = 0 |
|
|
|
iк = 0 |
iк ≠ 0 |
б) |
iк |
|
uк ≠ 0 |
uк = 0 |
|
после коммутации |
до коммутации |
||
|
1 |
2 |
||
|
|
|
uк |
Рис. 4.1 |
|
так же, как стационарную, характеризующуюся другим распределением токов, напряжений и электромагнитной энергии, нежели в исходной цепи. Переход из одного стационарного состояния в другое происходит не мгновенно, а с течением времени, что обусловлено наличием в цепи накопителей энергии (индуктивностей катушек и ёмкостей конденсаторов). Магнитная энергия катушек и электрическая энергия конденсаторов скачком измениться не могут, т.к. для осуществления этого необходимы источники, имеющие бесконечно большую мощность. Процессы, сопровождающие этот переход, на-
зываются переходными.
Строго говоря, цепь снова приобретает характер стационарной через неограниченно большое время после действия возмущения (t → ∞). Однако с достаточной для практических цепей степенью точности можно считать, что стационарное состояние наступает через некоторое конечное время, называемое временем переходного процесса (tпп). При этом токи и напряжения настолько приближаются к своим установившимся значениям, что расхождения между ними пренебрежимо малы.
Как было отмечено выше, возмущение действует так же не мгновенно, а в течение некоторого промежутка времени (рис. 4.2) ∆t = t2 – t1. Как правило, этот промежуток ∆t значительно меньше рассматриваемого времени переходного процесса (∆t < tпп), поэтому принято считать, что ∆t = 0, и моменты t1 и t2 сливаются в момент возмущения t0.
135
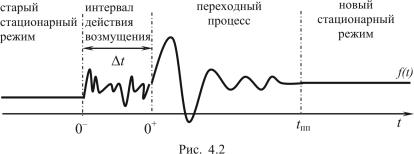
Значение исследуемой функции (тока или напряжения) f(t) не всегда одинаково в начале и в конце интервала возмущения. При устремлении этого интервала к 0 функция f(t) может изменяться скачкообразно. Таким образом, её значение до и после (или, как принято определять в математике, – слева и справа) момента возмущения t0 могут не совпадать. Это влечёт за собой необходимость различать моменты и 0− и 0+.
Как было сказано выше, к накопителям энергии относят индук-
тивности катушек (W = |
Li2 |
) |
и ёмкости конденсаторов (W = |
Cu2 |
) . |
|
|
||||
м |
2 |
|
эл |
2 |
|
|
|
|
|
Из условия корректности электрических цепей, которые не могут содержать источники, обладающие бесконечной мощностью, следуют
правила сохранения, называемые также законами коммутации, ис-
ключающие возможность скачкообразного изменения напряжения на ёмкости и тока в индуктивности в момент возмущения:
u (0− ) = u (0+ ), |
|
||
C |
|
C |
(4.1) |
i (0− ) = i |
|
(0+ ) . |
|
L |
|
||
L |
|
|
|
Начальные значения величин, сохраняющиеся неизменными в момент времени t = 0, называются независимыми начальными усло-
виями (значениями). Таковыми являются токи индуктивностей и напряжения на ёмкостях, подчиняющиеся правилам коммутации. Токи и напряжения сопротивлений, токи ёмкостей и напряжения на индуктивностях в момент коммутации могут изменяться скачком. Их вели-
чины после коммутации (t = 0+) называют зависимыми начальными
136
значениями. Последние не определяются непосредственно правилами сохранения, но всегда могут быть выражены через независимые начальные значения с помощью уравнений Кирхгофа, записанных для мгновенных значений токов и напряжений, действующих в послекоммутационной цепи для момента t = 0+.
4.2. КЛАССИЧЕСКИЙ МЕТОД РАСЧЁТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
Классический метод расчета переходных процессов основан на составлении и последующем решении (интегрировании) дифференциальных уравнений, составленных по законам Кирхгофа и связывающих искомые токи и напряжения послекоммутационной цепи и заданные воздействующие функции (источники электрической энергии). Преобразуя систему уравнений Кирхгофа, можно вывести итоговое дифференциальное уравнение относительно какой-либо одной переменной величины x(t):
a |
|
d n x |
+ a |
|
d n−1 x |
+ K+ a x = f (t) . |
(4.2) |
|
|
n−1 dt n−1 |
|||||
|
n dt n |
0 |
|
||||
Здесь n – порядок дифференциального уравнения и порядок цепи, величина положительных коэффициентов ak определяется параметрами пассивных элементов R, L, C цепи, а правая часть является функцией задающих воздействий.
В соответствии с классической теорией дифференциальных уравнений полное решение неоднородного дифференциального уравнения находится в виде суммы частного решения неоднородного дифференциального уравнения и общего решения однородного диф-
ференциального уравнения: |
|
x(t) = xчаст (t ) + xобщ (t ) . |
(4.3) |
Частное решение полностью определяется видом правой части f(t) дифференциального уравнения. В электротехнических задачах правая часть зависит от воздействующих источников электрической
137
энергии, поэтому вид xчаст (t) обуславливается (принуждается) источниками электрической энергии и называется принужденной составляющей xпр (t) .
Общее решение xобщ (t) однородного дифференциального урав-
нения зависит от корней характеристического уравнения, которые определяются коэффициентами дифференциального уравнения, и не зависит от правой части. В прикладных задачах электротехники xобщ (t)
не зависит (свободно) от воздействующих источников и по этой причине называется свободной составляющей xсв (t) и полностью опреде-
ляется параметрами пассивных элементов цепи, а физически – процессом перераспределения запасов энергии электрического и магнитногополей вреактивных элементах цепи.
Таким образом, любая искомая величина в переходном режиме
x(t) = xпр (t) + xсв (t) . |
(4.4) |
Свободную составляющую xсв (t) переходного процесса нахо- |
|
дят в виде |
|
n |
|
xсв = ∑ Ak e pk t , |
(4.5) |
k =1
где n – порядок цепи, совпадающий с порядком дифференциального уравнения; pk – корни характеристического уравнения (собственные числа цепи); Ak – постоянные интегрирования.
Собственные числа линейных цепей либо действительные отрицательные, либо комплексные с отрицательными вещественными частями (т.е. находятся в левой полуплоскости комплексных чисел). Поэтому xсв (t) носит преходящий (асимптотически затухающий до
нуля) характер:
xсв (t) → 0 .
n
В искомом решении x(t) = xпр + ∑ Ak e pk t надо уметь определять
k =1
величины xпр (t) , n, pk, Ak.
138
4.2.1. Определение принужденной составляющей
Уравнение (4.4) при t → ∞ принимает вид x(∞) = xпр (∞) , т.к. xсв (t) затухает до пренебрежимо малых размеров. Эти соображения позволяют утверждать: принужденная составляющая переходного процесса xпр (t) совпадает с соответствующей величиной в после-
коммутационном установившемся режиме и может быть получена изученными ранее методами.
Электрическая цепь для расчета принужденных составляющих от источников постоянных воздействий должна быть чисто резистивной (индуктивности заменяются короткозамкнутыми участками, а емкости – разомкнутыми). При наличии источников с гармоническими воздействиями расчет принужденных составляющих ведется символическим методом.
4.2.2.Определение порядка цепи n
Впростейших случаях низкопорядковых цепей можно руководствоваться следующей рекомендацией: порядок цепи определя-
ется количеством независимых реактивных элементов в этой цепи, другими словами, количеством независимых начальных условий.
Так, например, фрагменты цепей, приведенных на рис. 4.3, дают вклад в величину n:
139
В случае большого количества реактивных элементов в цепи |
||
порядок определяется оценочными формулами. Не претендуя на пол- |
||
ноту изложения, в качестве примера приведем одну из них: |
|
|
|
n = r −[aL +bL + aC +bC ], |
(4.6) |
где r – число реактивных элементов; аL, aC – число узлов, связывающих |
||
только индуктивные, или только ёмкостные токи соответственно; bL, |
||
bC – число контуров, проходящих только через реактивные элементы – |
||
индуктивности иёмкости соответственно, и не содержащие резисторов. |
||
|
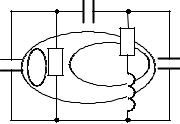
Рассмотрим применение форму- |
|
|
лы (4.6) на примере схемы (рис. 4.4): |
|
|
r = 4, aL = 0, aC = 0, bL = 0, bC = 1, сле- |
|
|
довательно, порядок цепи n = 4 – 1 = 3. |
|
|
Есть еще один способ определе- |
|
|
ния порядка цепи: если цепь не содер- |
|
|
жит особых контуров и особых сече- |
|
|
ний, то порядок цепи совпадает с коли- |
|
Рис. 4.4 |
чеством реактивных элементов. Под |
|
|
особыми контурами понимают конту- |
|
ры, охватывающие только емкости и источники ЭДС; под особыми |
||
сечениями понимают узлы, соединяющие только индуктивные токи |
||
или токи источников тока. Для рассматриваемой схемы количество |
||
реактивных элементов – 4, число особенных контуров – 1, |
число осо- |
|
бых сечений – 0. |
Таким образом, порядок цепи 4 – 1 = 3. |
|
Часто к быстрому результату при определении порядка цепи |
||
приводит следующая рекомендация: степень характеристического |
||
уравнения равна сумме порядков дифференциальных уравнений для |
||
независимых контуров, выбранных так, чтобы порядок дифферен- |
||
циальных уравнений для них был наименьшим. |
|
|
Так, цепь на рис. 4.4 имеет три независимых контура: внешний |
||
контур имеет нулевой порядок, левая ячейка-контур – первый поря- |
||
док и любой из оставшихся контуров (средняя ячейка, например) – |
||
второй порядок. Суммируя порядки этих контуров, получаем n = 3. |
||
140
