
книги / Основы теории цепей. Ч. 1
.pdfВысокий коэффициент мощности также желателен для уменьшения потерь при передаче энергии по линиям электропередачи. При данном значении Р приемника ток в линии тем меньше, чем больше
cos ϕ: I = |
P |
. |
|
||
U cos ϕ |
|
|
При расчетах электрических цепей находит применение реак-
тивная мощность Q:
Q =UI sin ϕ = I 2 ( X |
L |
− X |
C |
) =U 2 ( B − B |
), |
(3.54) |
|
|
L C |
|
|
которая положительна при индуктивном характере цепи (ϕ > 0) и отрицательна при емкостном характере цепи (ϕ < 0). Единицу мощности вприменениикизмерениюреактивноймощностиназываютвар.
Активная, реактивная и полная мощности связаны соотношениями
S 2 = P2 +Q2 ; |
Q |
= tgϕ. |
(3.55) |
|
|||
|
P |
|
|
Как следует из формул, для повышения коэффициента мощности приемника нужно уменьшать его реактивную мощность.
В то время как активная мощность определяет совершаемую работу или передаваемую энергию в единицу времени, полная и реактивная мощности не определяют ни совершаемой работы, ни передаваемой энергии в единицу времени. Однако в электроэнергетике по аналогии с понятием активной мощности приписывают реактивной мощности аналогичный смысл, рассматривают ее как мощность отдачи, получения или передачи некоторой величины, которую, хотя она и не является энергией, условно называют реактивной энергией, Wp = Qt (вар ч), на практике измеряют счетчиками.
Введем понятие комплексной мощности. Для того чтобы получить полную, активную и реактивную мощности из известных комплексов тока и напряжения, используют следующие соотношения:
111
S% =U& I =Ue jψu Ie− jψi =UIe j (ψu −ψi ) =UIe jϕ = (3.56) =UI cos ϕ+ jUI sin ϕ = P + jQ,
*
где S%– комплексная мощность, I – сопряженное значение тока. Отсюда видно, что действительная часть комплексной мощно-
сти равна активной мощности, а мнимая часть – реактивной мощности. Модуль комплексной мощности равен полной мощности S:
S% = I 2 Z =U 2 Y . |
(3.57) |
Рассмотримкомплексныемощностидляразличныхпотребителей:
– для активного сопротивления:
% |
& |
|
& |
|
jψi |
|
|
− jψi |
|
2 |
|
|
S =U I = IR I = Ie |
RIe |
= I |
R; |
|||||||||
|
|
|
||||||||||
P = I 2 R; Q = 0; |
|
|
|
|
|
|
|
|||||
– для индуктивного сопротивления: |
|
|
|
|||||||||
|
% |
|
& |
& |
|
|
2 |
jX L |
; |
|
|
|
|
S =U I |
= IjX L |
I = I |
|
|
|
||||||
|
P = 0; |
Q = I 2 X L ; |
|
|
|
|
|
|||||
– для емкостного сопротивления: |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
S% =U& |
I |
= I&(− jX C ) I |
= − jX C I 2 ; |
|
||||||||
P = 0; |
Q = −X C I 2 . |
|
|
|
|
|
||||||
3.4.4. Баланс мощности
(3.58)
(3.59)
(3.60)
Из закона сохранения энергии следует, что в любой цепи соблюдается баланс как мгновенных, так и активных мощностей. Сумма всех отдаваемых мощностей равна сумме всех получаемых мощностей. Рассмотрим, как соблюдается баланс для комплексных мощностей, а следовательно, и для реактивных мощностей.
112
Пусть общее число узлов схемы равно n. Запишем для каждого узла уравнение по I закону Кирхгофа для комплексных сопряженных токов:
* |
* |
* |
|
|
I12 |
+ I13 |
+K+ I1n = 0, |
|
|
* |
* |
* |
|
|
I 21 |
+ I 23 |
+K+ I 2n = 0, |
(3.61) |
|
|
|
|
|
|
K |
|
|
|
|
* |
* |
* |
= 0. |
|
I n1 |
+ I n2 |
+K+ I n,n−1 |
|
|
Эти уравнения записаны в общей форме в предположении, что каждый узел (здесь узел – место соединения не менее двух ветвей) связан с остальными n – 1 узлами. При отсутствии каких-либо ветвей соответствующие слагаемые в уравнениях становятся равными нулю. При наличии между какой-либо парой узлов нескольких ветвей число слагаемых соответственно увеличивается.
Умножим каждое уравнение (3.61) на комплексный потенциал узла, для которого составлено уравнение:
* |
|
* |
|
* |
|
|
|
ϕ&1 I12 |
+ ϕ&1 I13 |
+K+ ϕ&1 I1n |
= 0, |
|
|||
* |
|
* |
|
* |
|
|
|
ϕ&2 I 21 |
+ ϕ&2 I 23 |
+K+ ϕ&2 I 2n = 0, |
(3.62) |
||||
K |
|
|
|
|
|
|
|
* |
|
* |
|
* |
|
|
|
ϕ&n I n1 |
+ ϕ&n I n 2 |
+K+ ϕ&n I n,n−1 |
= 0. |
|
|||
Просуммируем все уравнения (3.62) с учетом того, что сопряженные комплексные токи входят в эти уравнения дважды (для двух раз-
|
|
|
|
|
|
|
|
|
личныхнаправлений), причем I 21 |
= −I12 ит.д. Врезультатеполучим |
|||||||
(ϕ1 |
|
|
+(ϕ1 |
|
|
+K+(ϕ1 |
|
1n +K |
−ϕ2 ) I12 |
−ϕ3 ) I13 |
−ϕn ) I |
||||||
& |
& |
|
& |
& |
|
& |
& |
(3.63) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
& |
& |
|
|
& |
& |
|
|
|
+(ϕn−1 |
−ϕ1 ) I n−1,1 |
+K+(ϕn−1 −ϕn ) I n−1,n = 0. |
||||||
113

В этом выражении столько слагаемых, сколько ветвей, и каждое слагаемое представляет собой комплексную мощность ветви S%i .
Таким образом, сумма комплексных получаемых мощностей во всех ветвях равна нулю. Полученное равенство выражает баланс мощностей S% = 0 . Из него следует равенство нулю в отдельности суммы определяемых активных и суммы определяемых реактивных мощностей.
Следует отметить, что взаимное
I& |
I& |
направление токов и напряжений на |
|
|
потребителях и на источниках проти- |
|
|
воположно, как показано на рис. 3.24. |
& |
U& |
Поскольку отрицательные получаемые |
U |
Рис. 3.24 |
мощности представляют собой мощно- |
|
сти отдаваемые, то можно утверждать, что суммы всех отдаваемых и всех получаемых реактивных мощно-
стей равны друг другу: |
S%пол = S%отд или S%ист = S%потр . |
|
|
||||
S%ист = ∑±E&i |
|
+ ∑±U&J |
|
= |
|
|
|
Ii |
Ji |
|
|
||||
i |
|
i |
i |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
(3.64) |
= ∑ P ± j∑Q = ∑ I 2 R |
|
|
∑ I 2 X L −∑ I 2 X C |
|
|
||
+ j |
|
|
|||||
|
|
123 |
|
|
144424443 |
|
|
|
|
P |
|
|
Q |
|
|
При равенстве сумм комплексных величин суммы их модулей в общем случае не равны друг другу. Отсюда следует, что для полных мощностей S баланс не соблюдается.
3.4.5. Метод контурных токов
Алгоритм расчета цепей гармонического тока методом контурных токов аналогичен рассмотренному при изучении цепей постоянного тока (глава 2.3.2) с поправкой на символический метод.
При решении задачи данным методом составляется система уравнений вида
114

|
|
|
Z |
|
I& |
= E& , |
(3.65) |
|
|
|
|
ij |
ii |
ii |
|
где |
|
|
– квадратная матрица комплексных сопротивлений, |
в ко- |
|||
Z ij |
|||||||
|
торой Z ij(i= j ) – собственное комплексное сопротивление, |
|
|||||
|
Z ij(i ≠ j ) |
– общее комплексное сопротивление i и j контуров; |
|
||||
I& – матрица-столбец контурных токов;
ii
E& – матрица-столбец контурных ЭДС.
ii
Пример. В цепи на рис. 3.25 гармонические источники ЭДС
e1 (t) = Em |
sin (ωt + ψe |
) → E&1 = |
Em1 |
|
e jψe1 , |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e2 (t) = Em |
|
sin ( |
ωt + ψe |
) → E& |
|
= |
Em2 |
e jψe2 . |
|
|
||||||||||||||||||||||
|
2 |
2 |
|
|
||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Составим |
|
|
систему |
|
урав- |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
нений для контурных токов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Z |
|
I& |
+ Z |
|
|
|
I& |
|
= E& |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
11 11 |
|
|
12 |
22 |
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Z |
|
I& |
+ Z |
22 |
I& |
|
= E& |
22 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
21 11 |
|
|
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z11 = R1 + R2 − jX C2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Z 22 = R2 + R3 + j ( X L |
− X C |
), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Z12 = Z 21 = −(R2 |
|
3 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
− jX C |
|
) |
, E&11 = E&1 , E&22 = E&2 , |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆ = |
|
Z |
11 |
Z |
12 |
|
, ∆ = |
|
E& |
|
|
|
Z |
12 |
|
, |
|
∆ |
|
= |
|
Z |
11 |
E& |
|
, |
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
& |
11 |
|
|
|
|
|
|
|
|
11 |
|
|||||||||||||||
|
|
Z |
|
Z |
|
|
|
|
|
|
1 |
|
|
|
|
Z |
|
|
|
|
|
2 |
|
|
Z |
|
& |
|
|
|||
|
|
21 |
22 |
|
|
|
|
|
|
E |
22 |
22 |
|
|
|
|
|
|
|
21 |
E |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I&1 = I&11 , I&2 = I&11 − I&22 , I&3 = I&22 .
115

3.4.6. Метод узловых потенциалов
Алгоритм расчета цепей гармонического тока методом узловых потенциалов аналогичен рассмотренному при изучении цепей постоянного тока (глава 2.3.3) с поправкой на символический метод.
При решении задачи данным методом составляется система уравнений вида
|
|
|
|
|
& |
& |
, |
(3.66) |
|
|
|
Y ij |
[ϕi ] = Jii |
||||
где |
Y ij |
|
– квадратная матрица комплексных проводимостей, в которой |
|||||
|
|
|
|
|
|
|
|
|
Y ij (i= j ) – собственнаякомплекснаяпроводимость,
Y ij (i≠ j ) – общая комплексная проводимость ветвей, соединяющих i и j узлы;
[ϕ&i ] – матрица-столбец потенциалов;
J& – матрица-столбец узловых токов.
ii
Для представленной цепи на рис. 3.25 система уравнений вырождается в одно уравнение, поскольку в цепи два узла.
ϕ&2 = 0, ϕ&1 = J&11 ,
Y 11
|
11 = |
1 |
+ |
|
|
1 |
|
|
+ |
|
1 |
|
|
|
|
J&11 |
= |
E& |
− |
|
E& |
||||||
Y |
|
|
|
|
|
|
|
|
|
|
, |
|
1 |
|
2 |
, |
|||||||||||
R1 |
R2 |
− jX C |
|
R3 |
+ jX L |
|
R1 |
R3 |
|
||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
+ jX L |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
3 |
|
||
|
|
|
−ϕ& |
+ E& |
|
|
|
|
ϕ& |
|
|
|
|
|
ϕ& |
|
+ E& |
2 |
|
|
|
|
|||||
I& |
|
= |
|
1 |
|
1 |
, I& |
= |
|
|
1 |
, |
I& |
= |
|
1 |
|
|
. |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
1 |
|
|
R1 |
2 |
|
|
R2 |
− jX C |
|
|
3 |
|
|
R3 |
+ jX L |
|
|
||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
3.4.7. Метод наложения
Алгоритм расчета аналогичен рассмотренному при изучении цепей постоянного тока (глава 2.3.4). Рассмотрим применение этого метода на примере схемы на рис. 3.25, которую можно заменить на две составляющие подсхемы (рис. 3.26):
116
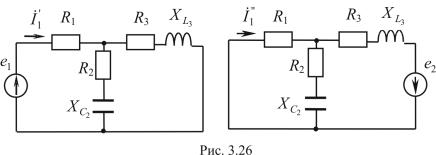
Составляющая тока I&1 от действия источника e1:
I&' |
= |
|
|
|
|
E& |
|
|
|
|
|
|
|
|
1 |
|
|
, |
|||
|
|
|
|
|
|
|
|
|||
1 |
|
|
|
(R2 − jX C )(R3 |
+ jX L ) |
|||||
|
|
R1 |
+ |
|||||||
|
|
|
|
|
2 |
|
3 |
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
R2 |
+ R3 |
+ j( X L |
− X C |
) |
|
|
|
|
|
|
|
|
|
3 |
|
2 |
|
составляющая тока I&1 от действия источника e2:
I&" = |
|
|
E&2 |
|
|
|
|
R2 − jX C2 |
|
, |
|
|
|
(R2 − jX C |
|
|
|
|
|||
1 |
|
|
R1 |
) |
|
R |
+ R − jX |
|
|
|
|
R3 + jX L |
+ |
|
|
|
|||||
|
|
|
2 |
1 |
2 |
C2 |
||||
|
R1 |
+ R2 − jX C2 |
|
|
|
|||||
3 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
полный ток
I&1 = I&1' + I&1" .
3.4.8. Метод эквивалентного генератора
Алгоритм расчета аналогичен рассмотренному при изучении цепей постоянного тока (глава 2.3.5).
Рассмотрим применение этого метода на примере определения тока I&1 схемы на рис. 3.25. На рис. 3.27 представлены схема цепи
в режиме холостого хода (обрыв потребителя в ветви, где ищется ток) и пассивная схема, в которой удалены источники (напоминаем, что источники исключаются из схемы по следующему правилу: источники ЭДС замыкаются накоротко, а ветви с источниками тока обрываются). Направление U&ХХ выбирается таким же, как искомый
117
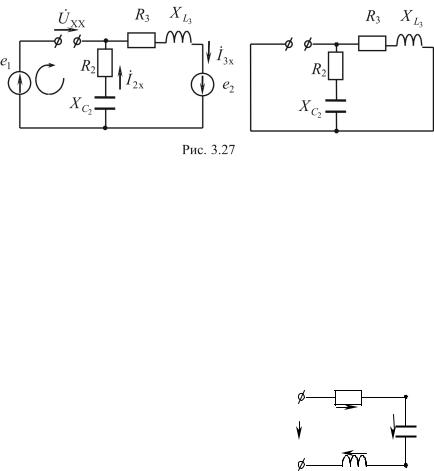
ток на заданной схеме (см. рис. 3.25). Для нахождения U&ХХ записывается II закон Кирхгофа для контура, содержащего U&ХХ , в соответствии с направлением обхода, указанным на рис. 3.27.
I& |
= I& |
, U& |
− I& |
(R − jX |
) = E& |
, I& |
= |
|
|
E&2 |
|
|
|
, |
|||||||
|
|
|
|
|
|
||||||||||||||||
2 x |
3x |
|
ХХ |
3x |
2 |
|
|
C2 |
|
|
1 |
|
3x |
|
R2 + R3 + j( X L |
− X C |
) |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
2 |
|
|
I& |
= |
U& |
|
|
= R , |
|
|
= |
(R2 |
− jX C |
)(R3 |
+ jX L |
) |
|
|
|
||||
|
|
ХХ |
, Z |
1 |
Z |
вх |
|
|
|
2 |
3 |
. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
|
Z1 |
+ Z вх |
|
1 |
|
|
|
R2 + R3 + j( X L3 |
− X C2 |
) |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
3.5. ЗАДАЧИ И ВОПРОСЫ |
|
|
|
|||
|
|
|
|
Типовые задачи |
|
|
|
|
|
Задача 1. |
|
|
|
|
|
|
|
||
Дано: электрическая цепь, изобра- |
|
R |
|
|
|||||
женная |
на |
рис. |
3.28, |
для |
которой |
a |
|
b |
|
|
|
||||||||
i(t) = 10sin(314t + 30°) , А; R = 5 Ом; С = |
U& |
U&R |
U&C |
С |
|||||
= 318 мкФ; L = 47,8 мГн. |
|
|
& |
||||||
|
|
|
|
|
|
|
U L |
|
|
Найти: |
|
|
|
|
d |
L |
|
c |
|
комплексные и мгновенные значе- |
|
|
|
||||||
|
Рис. 3.28 |
|
|||||||
ния напряжений на элементах схемы. |
|
|
|||||||
Построить векторную диаграмму тока и напряжений и топо- |
|||||||||
графическую диаграмму напряжений. |
|
|
|
|
|||||
118

Решение
1. Перейдем от мгновенного значения тока к комплексному
(п. 3.3.1).
Комплекс тока: I& = Im e jψi = 10 e j 30° = 7,07 30° А.
22
2.Найдем комплексные сопротивления реактивных элементов:
|
jωL = jX L = j314 47,8 10−3 = j15 Ом; |
|||||
− j |
1 |
= − jX C |
= − j |
1 |
= − j10 |
Ом. |
|
|
|||||
ωC |
314 318 10−6 |
|||||
3. По закону Ома в символической форме (п. 3.3.2) найдем комплексы напряжений на элементах схемы:
U&R = RI& = 5 7,07e j 30° = 35,35e j 30° В;
U&L = jX L I& = j15 7, 07e j 30° =106e j120° В;
U&C = − jXC I&= − j10 7,07e j 30° = 70,7e− j 60° В.
4. По известным комплексам напряжений найдем мгновенные значения напряжений:
uR (t) = 35,35 2 sin(314t + 30°) В; uL (t) = 106 2 sin(314t + 120°) В;
uC (t) = 70, 7 2 sin(314t − 60°) В. 5. Векторная диаграмма цепи. При построении векторной диа-
граммы (рис. 3.29) вектора напряжений и токов откладываются из начала координат комплексной плоскости.
119

U&R |
b +j |
|
При построении топогра- |
|
фической диаграммы (рис. 3.30) |
||
c |
U&C |
|
векторы напряжений на элемен- |
|
I& |
тах цепи строятся в той же после- |
|
U&L |
a |
довательности, в какой эти эле- |
|
|
U& |
|
менты включены в цепи. При |
|
|
этом каждой точке схемы соот- |
|
|
|
|
|
|
d |
+1 |
ветствует определенная точка |
|
на комплексной плоскости. Прин- |
||
|
Рис. 3.30 |
|
цип топографичности выполняет- |
|
|
|
ся только для напряжений. |
Построение топографической диаграммы начинают с того, что потенциал одной из точек цепи принимают за 0, а затем, обходя цепь в каком-либо направлении, подсчитывают потенциалы всех точек цепи и отображают их на комплексной плоскости.
|
ϕ&d |
= 0 ; |
|
|
|||
|
ϕ& |
c |
= ϕ& |
d |
+ jX |
L |
I& = 0 + j15 7,07e j 30° =106e j120° =106cos120°+ |
|
+ j106sin120° = −53 + j91,7 В; |
||||||
|
ϕ&b = ϕ&c + ( − jX C )I& = −53 + j91,7 − j10 7,07e j 30° = −53 + j91,7 + |
||||||
|
+70, 7 cos(−60°) + j70, 7 sin(−60°) = −53 + j91, 7 + 35,35 − j61, 24 = |
||||||
|
= −17, 65 + j30,46 В; |
||||||
|
ϕ& |
a |
= ϕ& |
b |
+ RI& = −17,65 + j30,46 +5 7,07e j 30° = −17,65 + j30,46 + |
||
|
|
|
|
|
|
||
|
iR |
|
|
R |
|
+35,35cos 30°+35,35sin 30° = |
|
|
|
|
|
= −17, 65 + j30, 46 +30, 62 + j17, 67 = |
|||
|
|
|
|
|
|
|
|
i |
|
iL |
|
L |
|
=12,97 + j48, 29 = 50e j 75° В. |
|
|
iC |
|
С |
|
Задача 2. |
||
|
|
|
Дано: электрическая цепь, изобра- |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
женнаянарис3.31, длякоторой |
|
|
|
|
|
|
iR =1sin(1000t) , А; R = 1 Ом; |
|
|
|
|
Рис. 3.31 |
||||
|
|
|
L = 1 мГн; С = 500 мкФ. |
||||
|
|
|
|
|
|
|
|
120
