книги / Теплопередача

♦для шара радиусом R

Формула (1.191) содержит оценку неравномерности регулярного температурного поля в любом теле, если для него известны величины λ, a , α , K, F и V.

Теория регулярного режима охлаждения справедлива не только для однородных простых тел, но также для любых сложных систем из разнородных тел.

Метод регулярного теплового режима использует простой математический аппарат и удобен как в эксперименте, так и при расчете процессов нестационарной теплопроводности.

Основные закономерности регулярного теплового режима были подробно исследованы Г.М. Кондратьевым [1], который раскрыл основные связи, существующие между темпом охлаждения m, с одной стороны, и физическими свойствами тела, его формой, размерами и условиями охлаждения – с другой. Это позволило разработать способы приближенного расчета нестационарных температурных полей, методы моделирования нестационарных процессов в сложных объектах, дать оценки неравномерности температурных полей в различных условиях

ит.д. На основе теории регулярного режима были предложены

иполучили широкое применение на практике новые методы оп-

81

циентов теплоотдачи α . Преимуществом таких методов является простота техники эксперимента, высокая точность получаемых результатов и малые затраты времени на проведение опытов.

1.6. РЕШЕНИЕ ЗАДАЧИ НЕСТАЦИОНАРНОЙ ТЕПЛОПРОВОДНОСТИ МЕТОДОМ КОНЕЧНЫХ РАЗНОСТЕЙ

В настоящее время существует много различных приближенных методов расчета задач теплопроводности, которые приводят к удовлетворительным для инженерной практики результатам. Приближенные методы решения задач чаще всего применяются в случае, когда точные аналитические методы расчета затруднительны. Рассмотрим решение задач теплопроводности методом конечных разностей (МКР) [7].

При численной реализации задачи МКР область непрерывного изменения аргумента заменяется его дискретным аналогом – сеточной областью. Непрерывная функция заменяется сеточной функцией, определенной только в узлах сетки. Исходные дифференциальные уравнения с соответствующими краевыми условиями аппроксимируются конечно-разностными уравнениями. Таким образом, решение исходной системы дифференциальных уравнений заменяется решением системы алгебраических уравнений.

Рассмотрим применение метода конечных разностей для решения задачи нестационарной теплопроводности плоской пластины, представленной выше (см. рис. 1.16):

82

Теплофизические параметры заданы.

Задача симметрична относительно начала координат по x = 0, поэтому для координаты x решение найдем в диапазоне от 0 до δ . Координата по времени изменяется от 0 до τ к.

На оси симметрии задается адиабатическое условие:

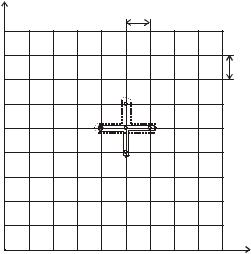
ωxτ = {xi = ihx , i =1, N +1; τj = jhτ, j =1, M +1} .

Шаг по координате x определяется по формуле hx = δ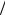 N , а по τ – по формуле hτ = τк M .

Вначале рассмотрим решение поставленной задачи МКР по явной схеме:

На рис. 1.23 шаблон явной схемы показан пунктирной линией.

83

Явная разностная схема обладает тем достоинством, что решение на верхнем временном слое получается сразу (без решения системы алгебраических уравнений) по значениям сеточных функций на нижнем временном слое, где решение известно (при j =1 значения сеточной функции формируются из началь-

ного условия). Но эта схема обладает недостатком, поскольку она является устойчивой лишь при условии 2аhτ 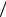hx 2 <1.

84

Решение дифференциального уравнения теплопроводности МКР, записанного по неявной схеме, имеет вид

Неявная схема абсолютно устойчива, но для определения температуры в узлах на верхнем временном слое требует решения системы алгебраических уравнений. Для этого уравнение (1.198) преобразуем к виду

Полученную систему алгебраических уравнений целесообразно решать методом прогонки [7].

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Сформулируйте закон Фурье.

2.Перечислите допущения, необходимые для вывода дифференциального уравнения теплопроводности.

3.Назовите закон, положенный в основу вывода дифференциальногоуравнения теплопроводности.

4.Запишитедифференциальноеуравнениетеплопроводности.

5.Перечислите условия однозначности для процессов теплопроводности.

85

6.Что задают и в каком случае отсутствуют начальные условия?

7.Перечислите виды граничных условий.

8.Запишите различные варианты постановки задачи стационарной теплопроводности плоской бесконечной стенки при отсутствии внутреннего источника тепла.

9.Запишите различные варианты постановки задачи стационарной теплопроводности цилиндрической бесконечной стенки при отсутствии внутреннего источника тепла.

10.Дайте определение тепловой изоляции и запишите расчетную формулу для вычисления критического диаметра тепловой изоляции.

11.Запишите постановку задачи теплопроводности полубесконечного массива с одной трубой, являющейся источником теплового воздействия на массив, и опишите методику определения линейной плотности теплового потока и поля температур.

12.Запишите постановку задачи нестационарного процесса теплопроводности плоской бесконечной стенки без внутренних источников тепла.

13.Дайте определение критериев Био и Фурье, поясните их физический смысл.

14.Проведите анализ аналитического решения задачи охлаждения плоской пластины.

15.Запишите постановку задачи нестационарного процесса теплопроводности плоского бесконечного цилиндра без внутренних источников тепла.

16.Перечислите стадии охлаждения тел, охарактеризуйте их.

17.Поясните структуру формулы для определения безразмерной избыточной температуры тела в стадии регулярного режима. Что общего в ней для тел разной формы?

18.Дайте определение, расчетную формулу и единицы измерения темпа охлаждения. Поясните особенности этой величины в стадии регулярного режима.

19.Постройте в полулогарифмических координатах зависимостьтемпературного напора отвремени длярегулярного режима.

86

2.КОНВЕКТИВНЫЙ ТЕПЛООБМЕН

ВОДНОРОДНОЙ СРЕДЕ

2.1.ОСНОВНЫЕ ПОЛОЖЕНИЯ И ОПРЕДЕЛЕНИЯ

Под конвекцией тепла понимают перенос тепла при перемещении макрочастиц подвижной среды (жидкости или газа) в пространстве из области с одной температурой в область с другой [1–5]. Конвекция возможна только в текучей среде, здесь перенос тепла неразрывно связан с переносом самой среды.

Подвижная среда может быть сжимаемой (газ, пар) или практически несжимаемой (капельная жидкость). Если скорость движения газа или пара существенно меньше скорости звука, то сжимаемостью можно пренебречь; в этом случае используют лишь один термин – жидкость, относя его к подвижной среде любой физической природы и агрегатного состояния [1].

Количество тепла, переносимое жидкостью через единицу поверхности по направлению нормали в единицу времени, называется плотностью конвективного теплового потока:

где v – скорость жидкости, м/с; ρ – плотность жидкости, кг/м3; i – энтальпия (теплосодержание), Дж/кг.

Для реальных жидкостей энтальпия является функцией температуры и гидростатического давления. В предположении о несжимаемости жидкости ( ρ = const ) с достаточной степенью

точности можно сказать, что энтальпия является функцией только температуры. Тогда

87

где c – удельная теплоемкость.

Так как конвекция всегда сопровождается процессами те-

здесь qтпр – плотность теплового потока за счет процессов теп-

лопроводности.

Конвективный теплообмен между потоком жидкости и поверхностью соприкасающегося с ним твердого тела называется конвективной теплоотдачей или просто теплоотдачей.

Одной из основных задач конвективного теплообмена является установление зависимости между плотностью теплового потока на границе поверхность–жидкость, температурой поверхности твердого тела и температурой жидкости. Эксперименты показывают, что при расчетах теплоотдачи можно использовать закон Ньютона–Рихмана:

где q – плотность теплового потока с поверхности твердого тела; α – коэффициент теплоотдачи; tс – температура поверхности твердого тела; tж – температура окружающей подвижной среды. Перепад температур tс − tж называется температурным напором.

В задачах конвективного теплообмена коэффициент теплоотдачи α является искомой величиной. Коэффициент теплоотдачи α зависит от скорости потока жидкости, температур поверхности тела и окружающей среды, теплофизических свойств подвижной среды, формы и размеров поверхности твердого тела и от многих других факторов.

88

По-разному протекает процесс теплоотдачи в зависимости от природы возникновения движения жидкости. По природе возникновения различают два вида движения: свободное и вынужденное. Если движение жидкости вызвано действием неоднородного поля массовых сил (гравитационных, магнитных, электрических), то говорят о свободной конвекции. Свободное движение также называется естественной конвекцией. В дальнейшем будет рассматриваться гравитационная свободная конвекция, вызванная неоднородностью распределения плотности среды, обусловленной неоднородностью температурного поля. При вынужденной конвекции движение жидкости происходит под действием внешних сил (за счет работы насоса, вентилятора, компрессора). Вынужденное движение в общем случае сопровождается свободным движением. Влияние последнего тем больше, чем больше перепад температур в жидкости и чем меньше скорость движения. При больших скоростях вынужденного движения влияние свободной конвекции пренебрежимо мало.

Большое влияние на теплоотдачу оказывают теплофизические свойства подвижной среды: коэффициент теплопроводности λ ; удельная теплоемкость с; плотность ρ . В движущейся среде появляется еще одно физическое свойство – вязкость.

Все реальные жидкости обладают вязкостью. Между частицами или слоями жидкости, движущимися с различными скоростями, всегда возникает сила внутреннего трения, противодействующая движению. Согласно закону вязкого трения Ньютона эта касательная сила, отнесенная к единице поверхности, пропорциональная изменению скорости в направлении нормали к этой поверхности [1, 2]:

здесь µ– коэффициент динамической вязкости (или коэффициент вязкости), Па с; s – удельная касательная сила трения (напряжение сдвига).

89

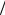
При ∂ v ∂ n= 1 s = µ , следовательно, коэффициент динами-

ческой вязкости численно равен касательной силе трения, приходящейся на единицу поверхности соприкосновения двух жидких слоев, скользящих друг по другу при условии, что на единицу длины нормали к поверхности скорость движения изменяется на единицу. Величина вязкости зависит от температуры и многих других факторов. Для капельных жидкостей величина незначительно связана с давлением и снижается по мере повышения температуры. Для газов значение с повышением температуры возрастает, а с увеличением давления изменяется слабо.

В уравнениях конвективного теплообмена часто используют кинематический коэффициент вязкости, м2/с,

Кинематическая вязкость для капельных жидкостей уменьшается при повышении температуры, так же как и , поскольку плотность ρ оченьслабо зависит оттемпературы.

На процесс конвективного теплообмена зачастую оказывает существенное влияние температурный коэффициент объемного расширения β, 1/К, который характеризует относитель-

ное изменение объема при изменении температуры на 1 К (при постоянном давлении):

здесь T = t + 273 – абсолютная температура, К; w – удельный объем, м3/кг.

Для газов, близких к идеальному, температурный коэффициент объемного расширения определяется по формуле

90