книги / Структурные механизмы деформирования и разрушения

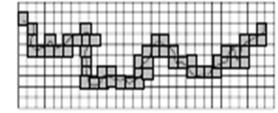
константа. В методе вертикальных сечений измеряется наклон зависимости ln L от ln или ln RL ( ) от ln . Это адекватно

определению фрактальной размерности D lim ln(N ( )) [2].

0 ln(1/ )

Согласно правилу Мандельброта, фрактальная размерность множества, состоящего из двух независимых фрактальных множеств P1 и P2, равна сумме фрактальных размерностей множеств P1 и P2. При этом истинная измеряемая фрактальная размерностьповерхностивычисляетсякаксредняя[5].

Метод подсчета ячеек (the box counting method) состоит в следующем: плоскость, в которой лежит исследуемый профиль, разбивают сеткой с площадью ячейки δ2 и определяют минимальное количество ячеек, необходимых для покрытия профиля N(δ) (рис. 1.5). Размерность определяется после проведения нескольких покрытий клетками различных размеров δ, подсчета длякаждогоизнихчислапокрывающих клетокN(δ) иопределения наклона зависимости lnN ~ ln δ [2]. Данная процедура производится для различных размеров ячеек. Число ячеек, необходимых для покрытия профиля, зависит от величины ячейки. Для фрактальной кривой с фрактальной размерностью D в этом случае выполняетсясоотношениеN(δ) ~ δ–D [2, 3].

δ

Рис. 1.5. Пример покрытия (темные клетки) для определения фрактальной размерности профиля методом подсчета числа ячеек

Метод подсчета числа ячеек может быть использован как для одномерного профиля, так и для трехмерной поверхности (вместо двумерных ячеек соответственно будут трехмерные).

11

Метод островов среза (the split-island method) состоит в получении зависимости A(P), где A – площадь, P – периметр «островов», получающихся при сечении анализируемой поверхности плоскостями, параллельными основной (средней) плоскости поверхности. Фрактальная размерность в этом случае определяется через наклон D′ графика данной зависимости в логарифмических координатах: D – 1 = 2/ D′ [2].

Метод переменного интервала (the variable bandwidth method) [6] применяется для вычисления показателя Херста одномерных профилей. Профиль длины L разбивается на отрезки длиной w, x0 − координата первой точки каждого

отрезка (рис. 1.6).

Рис. 1.6. К методу переменного интервала и методу моста [1]

На каждом отрезке вычисляется величина дисперсии высоты (standard deviation) S и размах K (разница между максимальным и минимальным значением высоты), затем данные величины усредняются по всем возможным отрезкам данной длины. Для самоафинных профилей данные функции на определенном спектре масштабов обнаруживают степенную зависимость от масштаба рассмотрения:

где K − максимальный размах; w − ширина окна; z – высота; x – координата; H − показатель Херста. Для дисперсии выполняется аналогичная зависимость:

где S − дисперсия; w − ширина окна; z − высота; x − координата; H − показатель Херста. По наклону линейного участка зависимости (1.3) или (1.4), построенной в логарифмических координатах, можно определить показатель Херста H.

Следует отметить, что данный метод применим на масштабах, не превышающих L/2, где L − длина анализируемого сигнала, и корректен при определении показателя шероховатости (показателя Херста) в интервале H [0; 1]. При получении значения показателя Херста, близкого к 0 или 1, необходимо проверить его другим методом [6]. Данный метод может быть распространен на трехмерный случай для анализа трехмерных образов поверхности. В общем случае при изучении многомерных профилей связь показателя Херста с фрактальной размерностью имеет вид

Dmax = 3 для поверхности; H − показатель Херста.

Данный алгоритм подобен методу моста (the bridge method) [6], предложенному Мандельбротом. Основное различие данных методов состоит в том, что в последнем вычитается линейный наклон между начальной и конечной точкой каждого отрезка.

На рис. 1.7 показана идентичность метода переменного интервала и метода моста [6] для модельного профиля с показателем шероховатости 0,5.

13

Рис. 1.7. Сравнение метода переменного интервала и метода моста для двух функций: а – дисперсии высоты (среднеквадратическое отклонение) S(w); б – размаха высот K(w) [6]

Для нахождения показателя Херста применяется также функция вида

где Z − структурная функция; z − высота; x − координата; w − ширина окна; H − показатель Херста.

В этом случае также H [0; 1]. Значение показателя Херста H = 1 соответствует регулярной поверхности, расположенной под углом к горизонтальной плоскости. Проведенные исследования показывают, что чем меньше H, тем более шероховата поверхность (тембольшефрактальнаяразмерность) [4].

Метод моста аналогичен методу длины шероховатости (roughness-length method), используемому в работе [1] для изучения скейлинга поверхностей разрушения горных пород. Автор [1] исследует зависимость дисперсии отклонений высоты профиля от локального линейного тренда на каждом интервале разбиения профиля (см. рис. 1.6):

где S − дисперсия; w − ширина окна; nw − общее число отрезков длины w; mi − число точек на интервале; Z − высота; (z j z ) −

отклонение высоты от локального линейного тренда; z − среднее значение отклонений высоты на интервале wi. Данная функция удовлетворяет следующим соотношениям:

где S − дисперсия; w − ширина окна; А – коэффициент пропорциональности; Н– показатель Херста. Значения H и A могут быть найдены из логарифмического графика зависимости функции S(w) как наклон линейного участка и пересечение с осью ординат, соответственно.

Автор работы [1] указывает на необходимость использования как минимум двух параметров для описания шероховатости поверхности − фрактальная размерность или связанный с ней показатель Херста в качестве величины, описывающей свойства скейлинга поверхности (показывающие, как меняется шероховатость с масштабом наблюдения) и значение параметра А, отражающего ориентацию (наклон) поверхности и характеризующий влияние скейлинга (перемасштабирования) на амплитуду шероховатости.

Как и метод подсчета ячеек, данный метод может быть применен для анализа трехмерных образов поверхности, алгоритм которого приведен в работе [1].

Метод определения вероятности повторения высоты

(return probability) [6]. Для каждой точки x0 профиля с высотой z(x0) ищется минимальное расстояние d до точки с такой же высотой z(x0+d) = z(x0). Статистическое распределение расстояний d, построенное для всех точек профиля, определяет распределение вероятности первого возвращения высоты p1(d). Для самоафинных профилейданнаявеличинаудовлетворяетсоотношению

15

где p1(d) − функция плотности распределения случайной величины d; Н – показатель Херста.

На рис. 1.7 представлено применение данного метода для профиля с индексом шероховатости H = 0,5, сгенерированного по методу, предложенному Воссом [6]. Суть данногометодасостоит в следующем: для двумерного профиля задаются значения высоты на концах отрезка zi и zj и вычисляется значение высоты на середине расстояния между ними как среднее zi + zj/2. На каждом k-м шаге генерирования флуктуации высоты ∆hk задаются из статистического распределения f(∆h) с нулевым средним значением и нормировочным параметром, пропорциональным длине рассматриваемого сегмента |i–j|.

Следует иметь в виду низкую достоверность точек, соответствующих большим расстояниям, которая вызвана возникающими шумами.

Вероятность повторения высоты для некоторой начальной точки означает вероятность нахождения точки с такой же высотой на расстоянии d. Когда рассматривают первую точку с равным значением высоты, говорят о вероятности первого повторения (the first return probability). При рассмотрении всех последующих пересечений имеет место мультивероятность. Данный график может быть построен в виде гистограммы.

Построение данной зависимости в логарифмических координатах позволяет подавить флуктуации графика, возникающие для больших расстояний. При этом выражение (1.9), описывающее скейлинг, преобразуется в выражение

Также следует упомянуть альтернативный метод определения мультивероятности, рассматривающий все (не только первое) пересечения профиля на данной высоте. Для него выражение (1.9) выглядит следующим образом:

16

В логарифмических координатах выражение для мультивероятности:

Данный метод используется, в частности, в работе [4].

Метод фурье-анализа профилей (power spectrum) [2, 6]

состоит в получении спектра мощности (суммы квадратов амплитуд) профилей поверхности. Для регулярных фракталов и статистически самоподобных структур в интервале самоподобия спектр мощности S(k) можно аппроксимировать зависимостью вида S(k) ~ k–B, где k − волновое число, а величина B связана с фрактальной размерностью D: B = 2(3 − D) [2].

В работе [6] построение фурье-спектра S(k) производится для автокорреляционной функции: K ( x) z(x x)z(x)

z(x x)z(x), где z − высота, x − координата. Для самоподобных профилей предполагается выполнение зависимости

где S(k) − спектр мощности Фурье; k − волновое число; H − показатель Херста.

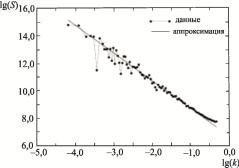
Анализ одномерного профиля с показателем Херста, равным 0,5, проведенныйданнымметодом, представленнарис. 1.8.

Рис. 1.8. Спектр мощности синтетического профиля L=16386 с показателем Херста, равным 0,5, построенный в зависимости от частоты k в логарифмических координатах [6]

17

В работе [7] исследование скейлинга поверхности тонких пленок проводится при помощи анализа автокорреляционной функции и функции перепада высот, построенных на основе данных атомно-силовой микроскопии. Построение одномерной автокорреляционной функции осуществляется для всех возможных пар профилей (zn+m, l и zn,l) матрицы данных N×M:

где Ax − автокорреляционная функция; rx − расстояние между двумя точками в направлении x; N и M − размеры анализируемых данных; n и m − индексы, задающие пару профилей; l − индекс точки в профиле.

Корреляционная функция перепада высот (height-height correlation function), позволяющая обнаружить зеренную структуру поверхностиматериала[7], выражаетсяформулой

где Zx − корреляционная функция перепада высот; rx − расстояние между двумя точками в направлении x; N и M − размеры анализируемых данных; n и m − индексы, задающие пару профилей; l − индекс точки в профиле. Данная зависимость имеет степенной характер Z(r) r2a, выражающийся в линейном росте графика функции log Z(r) от log r для малых r.

В работе [7] сделан вывод о том, что различие начальных наклонов графиков корреляционных функций перепада высот свидетельствует о различных микроструктурных процессах, протекающих в композитной и чистой пленке.

Корреляционная функция перепада высот, построенная по экспериментальным данным, была аппроксимирована зависимостью вида [7]:

18

где Z − корреляционная функция перепада высот; r – расстояние между парами точек на поверхности; w характеризует флуктуации высоты рельефа; a – показатель шероховатости; ξ − внутренняя корреляционная длина. Эти параметры являются важнейшими характеристиками морфологии поверхности.

На узком интервале масштабов выполняется соотношение D = 3–a, связывающее фрактальную размерность D и показатель шероховатости a. Внутренняя корреляционная длина характеризует максимальное расстояние, на котором высоты взаимосвязаны (коррелируют). Величина данного параметра разделяет коротко- и длиннокорреляционные взаимодействия интерфейса поверхности [7].

Для исследования скейлинга трехмерных структур поверхности разрушения горных пород в терминах фрактальной размерности в работе [8] используется метод покрытия поверхности проекцией сетки (projective covering method).

Рис. 1.9. Метод покрытия поверхности проекцией сетки:

а– разбиение фрактальной поверхности A проекцией сетки B;

б– k-я ячейка сетки

Исследуемая поверхность A разбивается спроектированной на нее сеткой В с размером ячейки δ (рис. 1.9). Высоты в узлах k-й ячейки обозначим через zak, zbk, zck и zdk, где первый индекс

19

соответствует индексу узла ячейки, второй индекс соответствует номеру ячейки. Тогда площадь шероховатой поверхности, заключеннуювданнойячейке, можновычислитьпоформуле

k 1

где AT − общая площадь поверхности; δ − размер ячейки; N − количество ячеек; Ak − площадь k-й ячейки.

Для фрактальной поверхности выполняется соотношение

где AT0(δ) определяет кажущуюся площадь шероховатой поверхности; D – фрактальная размерность поверхности.

В таблице представлены результаты анализа различных методов определения фрактальной размерности, проведенного в работе [6] для синтетического профиля различной длины с показателем Херста 0,5.

Максимальные значения погрешности вычисления фрактальной размерности для профилей различной длины