
книги / Надежность и диагностика компонентов инфокоммуникационных и информационно-управляющих систем
..pdf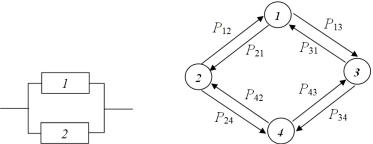
Рис. 7.1. Структура системы |
Рис. 7.2. Граф |
с параллельным соединением |
работоспособности системы |
Граф переходов по состояниям можно представить также матрицей переходов, используемой в дальнейшем для автоматизации расчетов:
|
P |
P |
P |
P |
|
|
11 |
12 |
13 |
14 |
|
P |
P21 |
P22 |
P23 |
P24 |
. |
ij |
P31 |
P32 |
P33 |
P34 |
|
|
|
||||
|
P41 |
P42 |
P43 |
P44 |
|
|
Как видно из определений, граф переходов аналогичен мар- |
|||||||||||||||
ковской цепи [2]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Вероятности P , P , P , P |
|
|
вследствие ординарности пото- |
||||||||||||
|
|
|
|
14 |
41 |
23 |
32 |
|
|
|
|
|
|
|
||
ка равны нулю. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Система уравнений, определяющая вероятности состояний, |
|||||||||||||||
имеет следующий вид: |
|
|
|
|
|
|
|
|
|
|
|
|
||||
P (t t) P (t) 1 |
|
P ( t) P ( t) |
|
P (t)P ( t) P (t)P ( t), |
|
|||||||||||
1 |
1 |
|
12 |
|
13 |
|
|
2 |
21 |
3 |
31 |
|
|
|||
P (t t) P (t) 1 |
|
P ( t) P ( t) |
|
P (t)P ( t) P (t)P ( t), |
|
|||||||||||
2 |
2 |
|
21 |
|
24 |
|
|
1 |
12 |
4 |
42 |
|
(7.7) |
|||
P (t t) P (t) 1 |
|
P ( t) P |
( t) |
|
P (t)P ( t) P (t)P ( t), |
|
||||||||||
3 |
3 |
|
31 |
|
34 |
|
|
1 |
13 |
4 |
43 |
|
|
|||
P (t t) P (t) 1 |
|
P ( t) P ( t) |
|
P (t)P ( t) P (t)P ( t). |
|
|||||||||||
4 |
4 |
|
42 |
|
43 |
|
|
2 |
24 |
3 |
34 |
|
|
|||
Уравнения системы, например первое, читается следующим образом: вероятность того, что система во время t + t будет на-
51

ходиться в первом состоянии, равна произведению вероятности того, что система в момент времени t находилась в первом состоянии, и вероятности отсутствия перехода во второе и третье состояние плюс вероятности того, что система находилась во втором или третьем состоянии в момент t, умноженные на вероятности перехода из этих состояний в первое за промежуток t.
Если t достаточно мало, то Pij ( t) ij t , где ij – интенсивность перехода из i-го состояния в j-е состояние.
Система, записанная в функциях интенсивностей, имеет следующий вид:
P (t t) P (t) P (t)( |
|
|
) t P (t) |
21 |
t P (t) |
31 |
t, |
|
||||||||||
1 |
1 |
1 |
12 |
13 |
2 |
|
3 |
|
|
|
||||||||
P (t t) P (t) P (t)( |
|
|
|
) t P (t) |
|
t P (t) |
|
|
|
t, |
|
|||||||
2 |
2 |
2 |
|
21 |
|
24 |
1 |
12 |
|
4 |
|
42 |
|
|
(7.8) |
|||
P (t t) P (t) P (t)( |
31 |
34 |
) t P (t) |
|
t P (t) |
43 |
t, |
|
||||||||||
3 |
3 |
3 |
|
|
1 |
13 |
|
4 |
|
|
||||||||
P (t t) P (t) P (t)( |
42 |
|
43 |
) t P (t) |
24 |
t P (t) |
34 |
t. |
||||||||||
4 |
4 |
4 |
|
|
2 |
|
3 |
|
|
|
|
|||||||
Перенос везде Pi (t) влево и деление уравнений на t приводит к получению в левой части
Pi |
(t t) Pi |
(t) |
|
Pi |
(t) |
. |
(7.9) |
|
t |
|
t |
||||
|
|
|
|
|
|||
При условии t 0 получаем
P (t) t dP (t) dt . |
(7.10) |
|
i |
i |
|
В окончательном виде система описывается следующими дифференциальными уравнениями:
dP (t) dt P (t) P (t) P (t) |
21 |
P (t) |
31 |
, |
|
||||||||||||
1 |
1 |
|
12 |
1 |
|
13 |
2 |
|
|
3 |
|
|
|
|
|||
dP (t) dt P (t) P (t) |
21 |
P (t) |
24 |
P (t) |
42 |
, |
|
||||||||||
2 |
1 |
12 |
2 |
2 |
4 |
|
|
|
(7.11) |
||||||||
dP (t) dt P (t) P (t) |
|
|
P (t) |
|
|
|
P (t) |
|
|
, |
|
||||||
31 |
34 |
43 |
|
||||||||||||||
3 |
1 |
13 |
3 |
3 |
4 |
|
|
|
|
||||||||
dP (t) dt P (t) |
24 |
P (t) |
34 |
P (t) |
42 |
P (t) |
43 |
. |
|
||||||||
4 |
2 |
|
3 |
|
4 |
|
4 |
|
|
|
|
||||||
При расчетах надежности систему уравнений составляют по графу работоспособности сразу в виде (7.11), минуя рассмотрен-
52
ные пояснительные этапы. Существует следующее правило составления системы. В левой части каждого уравнения записывается dPi (t) dt . В правой части уравнения содержится столько
dt . В правой части уравнения содержится столько
членов, сколько стрелок связано (входит и выходит) с данным состоянием. Каждый член равен произведению интенсивности потока , переводящего систему по данной стрелке, умноженной на вероятность того состояния, откуда стрелка исходит. Если стрелка входит в описываемое состояние, то произведению присваивается знак «+», если исходит, то знак «–».
Приведенное правило позволяет после получения графа работоспособности изделия составить систему дифференциальных уравнений, описывающих функционирование объекта.
На втором этапе в соответствии с приведенным правилом по графу работоспособности изделия можно составить систему дифференциальных уравнений, описывающих функционирование объекта.
На третьем этапе решаются уравнения системы и находятся искомые вероятности пребывания объекта в состояниях его работоспособности. Очевидно, что в рассматриваемом примере коэффициент готовности равен вероятности застать ответ в одном из трех работоспособных состояний:
K |
г |
P (t) P (t) P (t). |
(7.12) |
||
|
1 |
2 |
3 |
|
|
Решение системы может быть выполнено известными способами. В дальнейшем используется способ, основанный на преобразованиях Лапласа, переводящих систему дифференциальных уравнений в систему алгебраических уравнений:
ZP (Z ) P (0) P (Z ) |
P (Z ) |
P (Z ) |
21 |
P (Z ) |
31 |
, |
|
||||||||||
1 |
1 |
1 |
|
12 |
1 |
|
13 |
2 |
|
3 |
|
|
|
|
|||
ZP (Z ) P (0) P (Z ) |
|
P (Z ) |
21 |
P (Z ) |
24 |
P (Z ) |
42 |
|
, |
|
|||||||
2 |
2 |
1 |
12 |
2 |
2 |
4 |
|
|
|
(7.13) |
|||||||
ZP (Z ) P (0) P (Z ) |
|
P (Z ) |
|
|
P (Z ) |
|
|
P (Z ) |
|
|
, |
|
|||||
|
31 |
34 |
43 |
|
|||||||||||||
3 |
3 |
1 |
13 |
3 |
3 |
4 |
|
|
|
|
|||||||
ZP (Z ) P (0) P (Z ) |
24 |
P (Z ) |
34 |
P (Z ) |
42 |
P (Z ) |
43 |
. |
|
||||||||
4 |
4 |
2 |
|
3 |
|
4 |
|
4 |
|
|
|
|
|||||
53
Из системы алгебраических уравнений находятся вероятности пребывания системы в состояниях Pi (t) . С помощью обратных преобразователей Лапласа полученные вероятности Pi (t) приводят к искомому виду Pi (t) .
В момент включения системы начинается переходный процесс, который продолжается некоторое время до перехода системы в установившееся состояние. Рассмотрим, как рассчитывается переходный процесс для простейшего случая, когда система состоит из одного элемента.
Пример 1. Пусть необходимо определить надежность изделия, не имеющего резервирования, с заданными интенсивностями отказов = const и интенсивностью восстановления . Работоспособность системы описывается графом (рис. 7.3), принципы построения которого описаны в п. 2.3.2 учебного пособия [2], и в данном задачнике будут рассмотрены в следующем разделе. В данной теме граф считается построенным и характеризуется двумя состояниями: состояние 1 – состояние работоспособности; состояние 2 – состояние отказа; и двумя вероятностями: P1 – вероятность пребывания системы в состоянии 1; P2 – вероятность пребывания системы в состоянии 2.
Рис. 7.3. Граф работоспособности системы примера 1
Для составления системы дифференциальных уравнений по графу существует следующее правило: в левой части каждого уравнения записывается dPi (t) dt , в правой части уравнения со-
dt , в правой части уравнения со-
держится столько членов, сколько стрелок связано (входит и выходит) с данным состоянием. Каждый член равен произведению интенсивности потока , переводящего систему по данной стрелке, умноженной на вероятность того состояния, откуда стрелка
54
исходит. Если стрелка входит в описываемое состояние, то произведению присваивается знак «+», если исходит, то знак «–». Система дифференциальных уравнений может быть преобразована по Лапласу в систему алгебраических уравнений.
Описание графа по указанному правилу дает следующую систему уравнений:
ZP (Z ) P (0) P (Z ) P (Z ) , |
||||
1 |
1 |
|
1 |
2 |
ZP (Z ) P (0) P (Z ) P (Z ) . |
||||
2 |
|
2 |
1 |
2 |
Учитывая, что в момент включения t = 0 система должна
быть исправна ( P (0) 1, |
P (0) 0 ), получаем |
|||||
1 |
2 |
|
|
|
|
|
ZP (Z ) P (Z ) P (Z ) 1, |
||||||
1 |
1 |
|
|
2 |
|
|
ZP (Z ) P (Z ) P (Z ) 0. |
||||||
2 |
2 |
|
|
1 |
|
|
Отсюда |
|
|
|
|
|
|
|
P (Z ) |
P (t) |
|
|
||
|
1 |
|
, |
|
||
|
|
|
|
|||
|
2 |
|
Z |
|
|
|
|
|
|
|
|
||
P (Z ) |
|
Z |
|
. |
||
|
|
|
|
|||
|
|
|
|
|||
1 |
|
Z (Z ) |
|
|||
|
|
|
||||
Обратное преобразование вероятности P (Z ) требует приве-
1
дения ее к табличному виду. Для этого умножим и разделим
P (Z ) на ( + ): |
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P (Z ) |
|
|
Z |
|
|
|
( Z ) Z |
, |
||||||
|
|
|
|
|
|
|
|
|
||||||
1 |
|
Z ( Z ) |
Z (Z )( ) |
|||||||||||
|
|
|||||||||||||
|
P (Z ) |
1 |
|
|
|
|
1 |
|
|
. |
||||
|
|
|
|
|
|
|
||||||||
|
1 |
|
Z |
|
|
|
Z |
|||||||
|
|
|
|
|
|
|||||||||
Отсюда, учитывая, что 1/Z соответствует единичная функция
1(t), а 1 (Z ) соответствует |
e ( )t , получаем |
|||
P (t) |
|
|
|
e ( )t . |
|
|
|||
|
|
|||
1 |
|
|
|
|
|
|
|
||
55
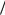
Анализом полученного выражения устанавливаем, что P (t)
1
при t не может быть ниже величины  ( ) . Эта посто-
( ) . Эта посто-
янная часть и является стационарным коэффициентом готовности изделия:
|
|
|
|
1 / Tв |
|
|
Т0 |
|
Kг . |
|
|
|
|
Т0 |
|
|
|||
|
1 / Тв 1 / Т0 |
|
Тв |
||||||
Постоянная времени |
экспоненты |
Тпэ 1 ( ). Переход- |
|||||||
ный процесс длится 3–4 Тпэ, после чего наступает установившийся режим.
Пример 2. Пусть интенсивность отказов ω = 0,25 ч–1, а интенсивность восстановлений = 0,95 ч–1. Построим график зави-
симости коэффициента готовности восстанавливаемого элемента от времени.
|
|
K |
|
(t) P (t) |
|
|
|
e ( ) t |
|||
|
|
г |
|
|
|
||||||
|
|
|
|
|
|||||||
|
|
|
|
|
Р |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
|
0,95 |
|
|
|
0, 25 |
|
e (0,25 0,95) t 0,79 0, 21e 1,2t . |
||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
||||||
|
0, 25 |
0, 4 |
0, 25 0,95 |
|
|
|
|||||
Сначала сведем результаты вычислений в таблицу:
t, ч |
Кг (t) |
t, ч |
Кг (t) |
0 |
1 |
3 |
0,796 |
0,5 |
0,905 |
3,5 |
0,793 |
1 |
0,853 |
4 |
0,792 |
1,5 |
0,824 |
4,5 |
0,791 |
2 |
0,809 |
5 |
0,791 |
2,5 |
0,800 |
5,5 |
0,790 |
|
|
6 |
0,790 |
Тпэ |
|
|
1 |
0,9 ч. |
|
|
|||
|
0,95 |
|||
|
0,25 |
|
||
По данным таблицы построим график (рис. 7.4).
56
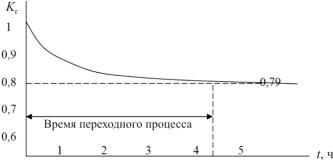
Рис. 7.4. Примерный вид нестационарного коэффициента готовности
Таким образом, коэффициент готовности в установившемся режиме равен 0,79. Время переходного процесса около 4 ч.
Варианты заданий для самостоятельных и расчетных работ
Задание: построить график зависимости коэффициента готовности восстанавливаемого элемента от времени и определить время переходного процесса, если заданы параметр потока отказов ω и интенсивность потока восстановления .
1. |
ω = 10–1 ч–1, |
= 0,3 ч–1 |
11. |
ω = 0,15 ч–1, = 0,5 ч–1 |
|
2. |
ω = 10–1 ч–1, |
= 0,4 ч–1 |
12. |
ω = 0,15 ч–1, = 0,6 ч–1 |
|
3. |
ω = 10–1 ч–1, |
= 0,5 ч–1 |
13. |
ω = 0,15 ч–1, = 0,7 ч–1 |
|
4. |
ω = 10–1 ч–1, |
= 0,6 ч–1 |
14. |
ω = 0,15 ч–1, = 0,8 ч–1 |
|
5. |
ω = 10–1 |
ч–1, |
= 0,7 ч–1 |
15. |
ω = 0,15 ч–1, = 0,9 ч–1 |
6. |
ω = 10–1 |
ч–1, |
= 0,8 ч–1 |
16. |
ω = 0,15 ч–1, = 1 ч–1 |
7. |
ω = 10–1 |
ч–1, |
= 0,9 ч–1 |
17. |
ω = 0,05 ч–1, = 0,3 ч–1 |
8. |
ω = 10–1 |
ч–1, |
= 1 ч–1 |
18. |
ω = 0,05 ч–1, = 0,4 ч–1 |
9. |
ω = 0,15 ч–1, |
= 0,3 ч–1 |
19. |
ω = 0,05 ч–1, = 0,5 ч–1 |
|
10. ω = 0,15 ч–1, = 0,4 ч–1 |
20. |
ω = 0,05 ч–1, = 0,6 ч–1 |
|||
57
21.ω = 0,05 ч–1, = 0,7 ч–1
22.ω = 0,05 ч–1, = 0,8 ч–1
23.ω = 0,05 ч–1, = 0,9 ч–1
24.ω = 0,05 ч–1, = 1 ч–1
25.ω = 0,07 ч–1, = 0,5 ч–1
26.ω = 0,07 ч–1, = 0,6 ч–1
27.ω = 0,07 ч–1, = 0,7 ч–1
28.ω = 0,07 ч–1, = 0,8 ч–1
29.ω = 0,07 ч–1, = 0,9 ч–1
30.ω = 0,07 ч–1, = 1 ч–1
В данной теме рассматривались надежностные характеристики восстанавливаемых систем: параметр потока отказов, параметр потока восстановлений, коэффициенты готовности и оперативный готовности.
Приведена методика количественной оценки указанных коэффициентов. Для закрепления материала предложены индивидуальные задания.
58
ТЕМА 8. РАСЧЕТ НАДЕЖНОСТИ СЛОЖНЫХ ВОССТАНАВЛИВАЕМЫХ СИСТЕМ
Как правило, сложные системы в целом и восстанавливаемые системы в частности в процессе эксплуатации характеризуются многообразием состояний: исправные, работоспособные (с некатастрофическими отказами элементов, не приводящими к отказу системы), приводящие к отказу системы и др.
В данной теме рассматривается метод расчета надежности сложных восстанавливаемых систем, основанный на составлении графа переходов систем (устройств) с восстановлением отказов в различные состояния работоспособности (граф работоспособности). Этот метод приведен в п. 2.3.2 и 2.3.4 учебного пособия [2].
На первом этапе составляется граф работоспособности объекта. Для этого определяются все состояния работоспособности с учетом блоков системы и устанавливаются интенсивности переходов по данным состояниям. Рассмотрим, например, систему с восстановлением из двух блоков (рис. 8.1), один из которых резервный. Будем считать, что используется резервирование постоянно включенным резервом, тогда система неработоспособна только при отказе сразу обоих блоков. Для такой системы могут быть выделены следующие состояния:
Состояние 1: блок 1 и блок 2 исправны (система исправна и работоспособна).
Состояние 2: блок 1 отказал, блок 2 исправен (система неисправна, но работоспособна, т.е. отказ одного из блоков не привел к отказу системы).
Состояние 3: блок 2 отказал, блок 1 исправен (система неисправна, но работоспособна).
Состояние 4: отказ блока 1 и блока 2 (отказ системы). Вероятность нахождения системы в i-м состоянии обознача-
ется Рi. Вероятность перехода из i состояния в j – Рij. Например, Р1 – вероятность пребывания системы в состоянии 1, Р2 – вероятность пребывания системы в состоянии 2, Р12 – вероятность пере-
59
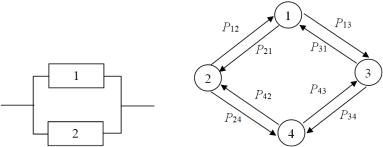
хода из состояния 1 в состояние 2 (т.е. вероятность отказа первого блока), Р21 – вероятность перехода из состояния 2 в состояние 1 (т.е. вероятность восстановления первого блока) и т.д. Граф работоспособности системы, построенный с учетом введенных обозначений, представлен на рис. 8.2.
Рис. 8.1. Структура системы |
Рис. 8.2. Граф работоспособности |
с восстановлением |
системы с восстановлением |
Вероятности P , P , P , P |
вследствие ординарности потока |
|||
14 |
41 |
23 |
32 |
|
равны нулю. Поясним данное утверждение на примере. Для того чтобы система перешла из состояния 1 в состояние 4, необходимо, чтобы в один момент времени произошли два события – отказали как блок 1, так и блок 2. Но это противоречит свойству ординарности потока, при выполнении которого в один момент времени может происходить только одно событие.
На втором этапе по графу работоспособности составляют систему уравнений.
Поскольку в данной теме мы рассматриваем только стационарный коэффициент готовности, то пропускаем этап составления системы дифференциальных уравнений и сразу переходим к системе линейных алгебраических уравнений. Существует следующее правило составления системы. В левой части каждого уравнения записывается 0. В правой части уравнения содержится столько членов, сколько стрелок связано (входит и выходит) с данным состоянием. Каждый член равен произведению интен-
60
