книги / Тестовые задания по курсу высшей математики. Ч. 1 Линейная алгебра. Векторная алгебра. Аналитическая геометрия

Задача 2.2.12

Если вектор m перпендикулярен векторам a = {2; −3;1} и b = {1;−2;3} , и удовлетворяет условию m c = 10 , где c = {1; 2;−7} , то

проекция вектора m на ось Oy , равна...

Решение 1-й способ

Введем обозначение m = { x; y; z} .

По условию векторы m и a перпендикулярны, следовательно, их скалярное произведение равно нулю, т.е. a m = 2x − 3y + z = 0 .

Аналогично из равенства нулю скалярного произведения векторов m и b получаем уравнение x − 2 y + 3z = 0 . Условие m c = 10 в координатной форме имеет вид x + 2 y − 7z = 10 . Таким образом, координаты искомого вектора m = { x; y; z} являются решением системы линейных алгебраических уравнений:

2x − 3y + z = 0,x − 2 y + 3z = 0,

x + 2 y − 7z = 10.

По условию задачи нужно найти проекцию вектора m на ось OY , следовательно, из данной системы определяем переменную y

41

2-й способ

Поскольку искомый вектор m перпендикулярен векторам a и b , то вектор m коллинеарен вектору d = a × b . Найдем векторное произведение векторовa и b .

По условию m c = 10 . Используя формулу скалярного произведения в координатной форме, получаем уравнение:

(−7λ ) 1+ (−5λ ) 2 + (−λ ) (−7) = 10.

Используя свойства скалярного произведения, имеем:

(5a + 3b) (2a − b) = 10a2 + 6b a − 5a b − 3b2 = 10a2 + a b − 3b2 = = 10 a 2 − 3 b 2 = 40 – 27 = 13.

Ответ: 13.

Задача 2.2.14

Векторное произведение a × b , где a = {4;5;1} , b = {1; 2;5} равно ...

1){23;−19;3} ,

2){23;19;3} ,

3){−23;−19;3} ,

4){−23;−19;−3}.

Решение

Ox равна ...

43

Задача 2.2.17

Если a = −i + j + 2k , b = 2i + 4 j + 2k , c = 3i + 2 j + k , то значение выражения 11 b × (c + a) равно ...

Решение

Найдем вектор c + a .

Так как c = {3;2;1} , a = {−1;1;2} , то c + a = {2;3;3} .

смешанное произведение равно нулю. Найдем смешанное произведение векторов a, b, c .

Приравнивая смешанное произведение к нулю, получаем n = −1.

Ответ: –1.

45

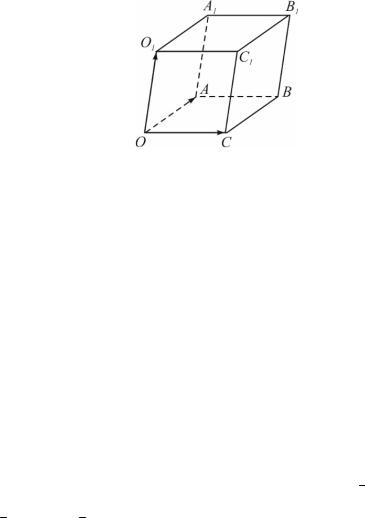
Задача 2.2.19

Если вершины параллелепипеда OABCO1 A1B1C1 имеют коорди-

наты O(0;0;0) , A(1;1;1) , O1 (2;0;3) , C (1;0;6) , то его объем равен ...

Решение

Рис. 2.15

___ ___ ___

Рассмотрим три вектора OA , OC , OO1 . Абсолютная величина

___ ___ ___

смешанного произведения векторов OA , OC , OO1 равна объему

параллелепипеда, построенного на этих векторах, как на трех пересекающихся ребрах.

Объем параллелепипеда равен 9.

Ответ: 9.

Задача 2.2.20

Объём пирамиды, построенной на векторах a = {1; 2; m} , b = {1; 2;0} , c = {1; m;0} , равен 43 , если положительное m равно ...

46

Решение

Объем пирамиды, построенной на векторах a, b, c , можно вы-

в формулу для вычисления объема пирамиды, получаем уравнение: 16 m2 − 2m = 43 . Отсюда m2 − 2m = 8 или m2 − 2m = −8 . Первое уравнение имеет корни: m1 = 4 , m2 = −2 . Второе уравнение корней

не имеет. Условию задачи удовлетворяет m1 = 4 .

Ответ: 4.

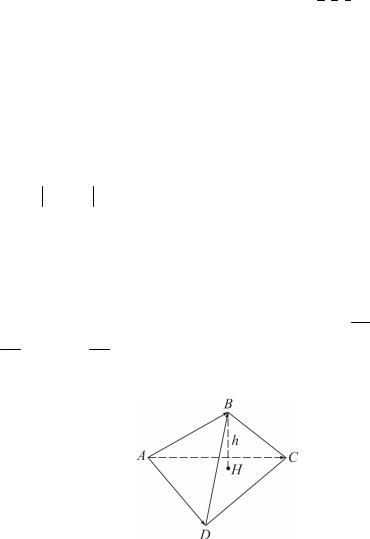
Задача 2.2.21

Высота BH пирамиды, построенной на векторах AB = {1;2; 4} ,

AC = {1; 2;0} , AD = {1; 4;0} , равна ...

Решение

Рис. 2.16

47

Найдем объем и площадь основания пирамиды:

Таким образом, h = 3Vпир = 4 = 4.

Sосн 1

Ответ: 4.

48

III. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

§3.1. Вопросы тестовых заданий

Вопрос 3.1.1

Ax + By + C = 0 на плоскости.

Решение

Рис. 3.1

Всякое уравнение первой степени Ax + By + C = 0 относительно текущих координат x и y определяет на плоскости прямую l . Вектор n = { A ; B} перпендикулярен прямой l (рис. 3.1) и называется

нормальным.

Вопрос 3.1.2

Тангенс угла наклона прямой к оси абсцисс называется ... … прямой.

Решение

Тангенс угла наклона прямой к оси Ox называется угловым коэффициентом прямой ( k = tg ϕ ). Угол ϕ отсчитывается от

оси Ox к прямой против часовой стрелки (рис. 3.2).

49

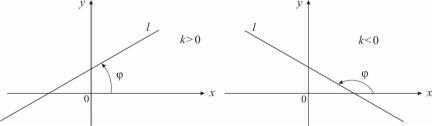
Рис. 3.2

Вопрос 3.1.3

Уравнение прямой, проходящей через точки M1 (x1; y1 ) и M2 (x2 ; y2 ) , имеет вид

1)y = kx + b,

2)y − y1 = k (x − x1 ),