книги / Моделирование функционирования изделий и технологических процессов в системах компьютерной математики

Помимо функций в СКМ для записи математических выражений используются специальные знаки – операторы. К примеру, вычисление квадратного корня часто записывается с помощью его специального знака. Достаточно хорошо известны операторы сложения, вычитания, умножения, деления и некоторые другие. Операторы обычно используются с операндами в виде констант или переменных.

Можно сказать, что основная сложность изучения пакетов компьютерной математики (как в области численных решений задач, так и в области символьных вычислений) связана не столько с математикой, сколько с проблемой общения пользователя и компьютера. Представления одних и тех же математических объектов для человека и компьютера иногда сильно отличаются.

Поэтому базовые знания и навыки работы с СКМ при решении конкретных задач обязательно должны быть дополнены сведениями из встроенных справочников, работа с которыми является, повидимому, наиболее доступным и эффективным средством для изучения как синтаксиса, так и используемых команд и функций [6, 7].

Современные математические пакеты (СКМ) обладают развитыми системами помощи пользователю, содержащими не только инструкции по работе с входным языком программ, но и многочисленные примеры решения конкретных задач, которые пользователь может применять в качестве шаблонов и адаптировать к реализации своих вычислений путём изменения исходных данных. В системе MathCAD таким центром поддержки пользователей является

«Resources Center» (центр ресурсов).

Контрольные вопросы и задания

1.Назовите основные элементы интерфейса СКМ MathCAD

иих функциональное назначение.

2.Что такое «функция» в СКМ MathCAD?

3.Что такое «оператор» в СКМ MathCAD?

4.Опишите структуру документа СКМ MathCAD. Из каких блоков он может состоять?

5.Что такое системы компьютерной математики? В чём преимуществоих использования длярешения научно-техническихзадач?

41

6.Перечислите основные элементы входного языка СКМ MathCAD и их функциональное назначение.

7.Каков порядок выполнения операций СКМ MathCAD?

8.К какому типу относится входной язык СКМ MathCAD и как он в целом работает?

9.Перечислите названия специальных панелей инструментов СКМ MathCAD и опишите их функциональное назначение.

10.Опишите типовую структуру СКМ и функциональное назначение её частей.

11.Выполните в СКМ MathCAD ввод исходных данных и построение графиков функций:

42

РАЗДЕЛ 3. РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ И СИСТЕМ УРАВНЕНИЙ

C ИСПОЛЬЗОВАНИЕМ СИСТЕМЫ MathCAD

3.1.Функции решения нелинейных уравнений

иих аргументы

Как известно, многие уравнения и системы уравнений не имеют аналитических решений. В первую очередь это относится к большинству трансцендентных уравнений. Доказано также, что нельзя построить формулу, по которой можно было бы решить произвольное алгебраическое уравнение степени выше четвёртой. Однако такие уравнения могутрешаться численнымиметодамис заданнойточностью.

Для простейших уравнений вида f (x) = 0

решение в MathCAD находится с помощью функции root. Функция root(f(x), х) возвращает значение х, принадлежащее отрезку [a, b], на котором находится решение, при котором выражение или функция f(х) обращается в 0. Обязательные аргументы этой функции – сама функция f(x) и независимая переменная x – должны быть скалярами. Также в число аргументов функции root могут входить границы интервала, на котором следует искать решение. Функция возвращает число – значение корня уравнения. Для её применения следует сначала задать начальное приближение для решения (рис. 11). К недостаткам применения данной функции относится то, что в результате решения может быть получен только один корень. Если уравнение имеет несколько корней, то для определения их всех функцию нужно использовать несколько раз.

Для нахождения корней выражения, имеющего вид an xn + an−1xn−1 + ... + a1x + a0 = 0,

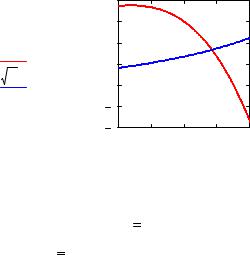
лучше использовать функцию polyroots, нежели root. В отличие от функции root, функция polyroots не требует начального приближения и возвращает сразу все корни, как вещественные, так и комплексные

(рис. 12).

43

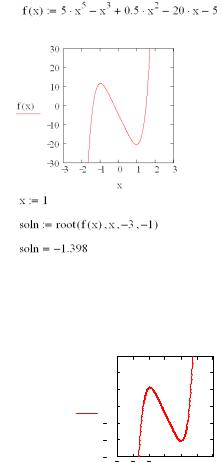
Рис. 11. Решение уравнения вида f(x) = 0 с помощью функции root

f (x) := 5 x5 − x3 + 0.5 x2 − 20 x − 5

Рис. 12. Решение уравнения вида f(x) = 0 с помощью функции polyroots

44

Функция polyroots(v) возвращает корни полинома степени n. Коэффициенты полинома находятся в векторе v длины (n+1). Возвращается вектор размером n, состоящий из корней полинома. Аргумент – вектор v, содержащий коэффициенты полинома. Вектор v задаётся стандартными операторами работы с векторами и матрицами.

3.2. Функции решения систем уравнений и их аргументы

MathCAD даёт возможность решать также и системы уравнений. Результатом решения системы будет численное значение искомых корней. К системам уравнений приводят задачи, в которых требуется определить параметры функционирования машин или протекания процессов, удовлетворяющиесразу несколькимусловиям (ограничениям).

Системы линейных уравнений удобно решать с помощью функции lsolve (рис. 13):

lsolve(А, b)

I := lsolve(A , B)

4.72

−0.32 I = −1.762.64

Рис. 13. Решение системы линейных уравнений с помощью функции lsolve

45

Эта функция возвращает вектор решения x, который удовлетворяет решению линейной системы Ах = B. При этом реализуется решение модифицированным методом Гаусса [12].

Аргументы: А – квадратная несингулярная матрица левой части системы, B – вектор правых частей уравнений.

Для решения произвольной системы нелинейных уравнений необходимо выполнить следующее:

1.Задать начальное приближение для всех неизвестных, входящих в систему уравнений. MathCAD решает систему с помощью итерационных методов [12, 13].

2.Задать ключевое слово Given. Оно указывает MathCAD, что

далее следует система уравнений.

3.Ввести уравнения и неравенства в любом порядке. При этом используется панель инструментов «Boolean» («Логическая»).

4.Ввести функцию Find независимо либо в виде переменной.

Given

x3 − 2 x2 + 0.5 x − 7 + y 0 y2 − exp(x) 0

2.418 Find(x , y) = 3.35

Рис. 14. Решение системы нелинейных уравнений с помощью функции Find

46

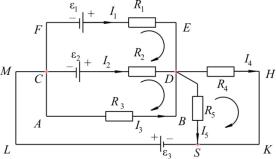
Функция Find(z1, z2, . . .) возвращает точное решение системы уравнений. Число аргументов данной функции, которые являются неизвестными и должны обозначаться точно так же, равно числу неизвестных системы.

Ключевое слово Given, уравнения и неравенства, которые следуют за ним, и какое-либо выражение, содержащее функцию Find, называют блоком решения уравнений (рис. 14).

3.3.Примеры решения алгебраических

итрансцендентных уравнений

Приведём примеры решения задач с помощью рассмотренных функций:

1. Задача из области электротехники. При заданных значениях ЭДС и сопротивлений рассчитать значения токов в ветвях (рис. 15).

ε1 = 10 В, ε2 = 7 В, ε3 = 15 В, R1 =15 Ом,

R2 =10 Ом,

R3 = 25 Ом, R4 = 14 Ом, R5 = 6 Ом

Рис. 15. Схема электрической цепи

По законам Кирхгофа запишем уравнения для узла D и конту-

ров CFED, ACDB, DHKS и ACMLSDB:

I1 + I2 + I3 − I4 − I5 = 0;

I1R1 − I2 R 2 = ε1 − ε2 ;

I2 R 2 − I3 R3 = ε2 ;

I4 R 4 − I5 R5 = 0;

I3 R 3 + I5 R5 = ε3 ,

где I – токи в ветвях; ε – ЭДС; R – сопротивления.

47

На рис. 16 представлено решение этой задачи с помощью функции lsolve.

Рис. 16. Расчёт токов с помощью функции lsolve

2. Задача из области механики. Показанный на рис. 17 криво- шипно-шатунный механизм описывается уравнением, задающим соотношения между размерами его конструкции а1, а2 и а3 и координатами ϕ и S его звеньев:

2a1S cos(ϕ) + 2a1a3 sin(ϕ) − a12 + a22 − a32 = S2 .

Механизм должен удовлетворять следующим условиям:

Рассчитать размеры конструкции.

48

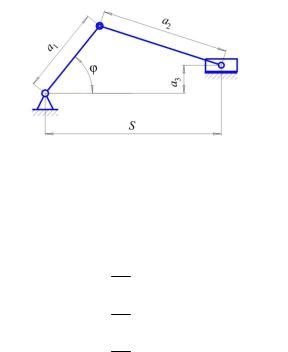
Рис. 17. Схема кривошипно-шатунного механизма

Уравнения составлены с учётом условий, которым должен удовлетворять механизм.

Рис. 18. Определение геометрических параметров кривошипно-шатунного механизма

49

Если уравнение имеет параметр, от которого зависит решение, то при расчётах можно выразить искомый корень непосредственно через параметр. Для этого вместо того, чтобы решать уравнение для каждого нового значения параметра, следует функцию поиска корня задать как функцию параметра за счёт того, что один из аргументов функции зависит от данного параметра. Таким образом, за одно действие можно получить общую зависимость решения от параметра задачи. В системе MathCAD такие операции можно выполнить стандартными средствами задания функциональных зависимостей с помощью обычных функций решения систем уравнений. Рассмотрим такой пример.

3. Задача из области механики. С какой максимальной скоростью тепловоз, развивающий силу тяги F = 250 кН, может равномерно вести состав массой 20 т? Сила сопротивления воздуха Fс = A V+B V3, где V – скорость движения. Коэффициенты имеют следующие значения: А = 100 Н с/м, В = 300 Н с3/м3. Коэффициент трения μ колес о рельсы 0,002. Ускорение свободного падения g = 9,81 м/с2. Исследовать, как будет меняться скорость при изменении силы тяги F.

Уравнение, котороетребуется решать вданном случае, имеет вид

F − Fc − Fтр = 0,

где Fтр – сила трения.

С учетом того, что сила трения Fтр = тgμ , получаем:

F − AV − BV 3 − mgμ = 0.

На рис. 19 представлено решение задачи. При этом в функцию поиска корня введена зависимость от параметра F, сама же исходная функция представлена как функция двух аргументов. Решение получено в форме функциональной зависимости величины максимальной скорости от силы тяги F и проиллюстрировано графически.

50