книги / Математические основы теории систем. Методы оптимизации

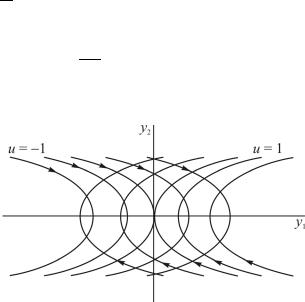
Для и = – 1 аналогичным образом получаем: y2 = −t + A1,

y1 = − t2 + A1t + A2 = −0,5y22 + S2 . 2

Меняя значение S2, строим семейство фазовых траекторий для

и = –1. В этом случае dy2 = u < 0 , т.е. со временем значение коорди- dt

наты y2 убывает. В соответствии с вышеизложенным указано направление движения по траектории.

Рис. 5.3. Семейство фазовых траекторий к задаче о максимальном быстродействии

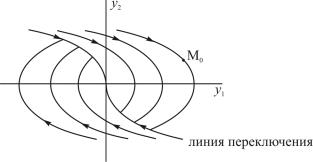
В данной задаче требуется попасть из любой точки фазовой плоскости в начало координат. Траектории, проходящие через конечную точку (в данном случае через начало координат), образуют линию переключения (рис. 5.4). Допустим, начальная точка лежит выше линии переключения. Дляэтогослучаясначала и= – 1, затем и= 1.

Найдем время прихода в конечную точку. Для примера взята точка М0 на рис. 5.4.

1.Находим начальную и конечную траектории движения. Для

рассматриваемого случая начальная траектория y1 = –0,5y22 + S2, конечная траектория y1 = 0,5y22.

2.Подставляем координаты начальной точки y1(0) = y10, y2(0) =

=y20 в уравнения для фазовых координат при управлении, и = –1, находим постоянные A1, A2, S2:

141

Рис. 5.4. Возможные траектории при движении к началу координат

3. Нахождение времени переключения. Для этого используем равенство

y1 = 0,5 y22 (уравнение линии переключения):

4. Находим координаты от точки переключения:

y2Π = −tΠ + A1.

5. Находим коэффициенты K1 и K2, решив систему уравнений:

y2Π = −tΠ + K1.

6. Находим время прихода в конечную точку из уравнения: y2k = 0 = tk + K1, tk = −K1.

142

Задания для самостоятельного решения

Дано:

1. Объект управления, описывающийся дифференциальным уравнением

= d2 y U dt2 ,

где у – выходной параметр; U – функция управления.

2. Критерий оптимальности – максимальное быстродействие, т.е.

T

Q = ∫dt = T → min ,

0

где [0; T] – временной интервал управления.

3.Ограничение на управление: U ≤ 1.

4.Координаты начальной точки, в которой находится объект управления [У0 ,У&0 ] , где

5. Конечная точка – начало координат фазовой плоскости. Требуется: найти такую функцию управления U (t) , при которой

объект из начальной точки в конечную (начало координат фазовой плоскости) переходит за минимальное время.

Задачу целесообразно решать в следующей последовательности: 1. Уравнение объекта представить в виде системы дифференци-

альных уравнений в фазовых координатах:

У&1 = f1 (t, y1, y2 ), У&2 = f2 (t, y1, y2 ).

2.К полученной системе дифференциальных уравнений добавить уравнение У&0 = 1.

3.К найденной системе применить принцип максимума Понтря-

гина.

143

4. Найти функции: y1 = f1 (t), y2 = f2 (t), y1 = f3 ( y2 ).

5.На фазовой плоскости ( y1, y2 ) отметить начальную точку.

6.Определить начальную траекторию движения, а затем момент времени переключения.

7.Найти конечную траекторию движения.

Пример

Дан объект второго порядка, имеющий два нулевых корня. Найти оптимальное по быстродействию управление, при котором объект из любой точки фазовой плоскости переходил бы в начало координат за минимальное время.

Решение.

Первоначальное управление u = –1, после переключения u = 1.

144

1.Находятся начальная и конечная траектории движения. Для рассматриваемого случая:

начальная траектория y1 = – 0,5 y22 + S2, конечная траектория y1 = 0,5 y22.

2.Подставляются координаты начальной точки y1(0) = y10,

3. Нахождение времени переключения. Для этого используется равенство y1 = 0,5 y22 (уравнение линии переключения):

−tп2 + A1tп + A2 = 0,5(−tп + A1 )2 , 2

tп = 1.

4. Находятся координаты точки переключения:

5. Находятся коэффициенты K1 и K2 , решив систему уравнений:

y1п = tп2 + K1tп + K2 , 2

y2п = tп + + K1,

K1 = −2

K2 = 2.

145

6. Находится время прихода в конечную точку из уравнения y2k = 0 = tk + K1,

tk = K1,

tk = 2.

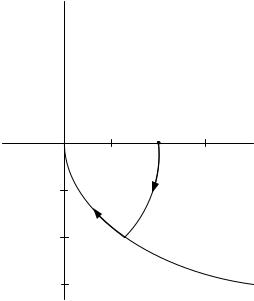
Оптимальная траектория движения изображена на рис. 5.5.

y2

y1

0.51.0 1.5

-0.5

-1.0

-1.5

Рис. 5.5. Оптимальная траектория движения

146

СПИСОК ЛИТЕРАТУРЫ

1.Панов В.А. Математические основы теории систем. Методы оптимизации. – Пермь: Изд-во Перм. гос. техн. ун-та, 1999. – 76 с.

2.Афанасьев В.Н., Колмановский В.Б., Носов В.Р. Математическая теория конструирования систем управления. – М.: Высшая шко-

ла, 1989. – 447 с.

3.Бронштейн И.Н., Семендяев К.А. Справочник по математике. –

М.: Наука, 1980. – 976 с.

4.Кротов В.Ф. Основы теории оптимального управления / под ред. В.Ф. Кротова. – М.: Высшая школа, 1990. – 430 с.

5.КузнецовА.В., Сакович В.А., Холод Н.И. Высшая математика. Математическое программирование. – Минск, 1994. – 286 с.

6.Лесин В.В., Лисовец Ю.П. Основы методов оптимизации. –

М., 1995. – 344 с.

7.Основы теории оптимизации / В.Д. Ногин [и др.]. – М.: Выс-

шая школа, 1986. – 384 с.

8.Сакович В.А. Исследоване операций. – Минск, 1984. – 256 с.

147

Учебное издание

Панов Владимир Александрович

МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ СИСТЕМ. МЕТОДЫ ОПТИМИЗАЦИИ

Учебное пособие

Корректор И.Н. Жеганина

––––––––––––––––––––––––––––––––––––––––––––––––––––––––

Подписано в печать 8.10.2011. Формат 60×90/16. Усл. печ. л. 9,5. Тираж 100 экз. Заказ № 175/2011.

––––––––––––––––––––––––––––––––––––––––––––––––––––––––

Издательство Пермского национального исследовательского

политехнического университета.

Адрес: 614990, г. Пермь, Комсомольский пр., 29, к. 113.

Тел. (342) 219-80-33.

148