
книги / Методические указания к проведению практических занятий по разделу математическая статистика дисциплины Основы системного анализа и математической статистики
..pdfМинистерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Пермский национальный исследовательский политехнический университет»
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ПРОВЕДЕНИЮ ПРАКТИЧЕСКИХ ЗАНЯТИЙ
ПО РАЗДЕЛУ «МАТЕМАТИЧЕСКАЯ СТАТИСТИКА» ДИСЦИПЛИНЫ «ОСНОВЫ СИСТЕМНОГО АНАЛИЗА И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ»
для студентов магистратуры по направлению 08.04.01«Строительство»
Издательство Пермского национального исследовательского
политехнического университета
2017
2
Составители: М.А. Макагонова, Н.В. Рогова, О.А. Федосеева
УДК 519.22 М54
Рецензент:
кандидат физ.-мат. наук, С.М. Седова (Пермский национальный исследовательский политехнический университет)
М54 Методические указания к проведению практических занятий по разделу математическая статистика дисциплины «Основы системного анализа и математической статистики» для студентов магистратуры по направлению 08.04.01 «Строительство» / сост. М.А. Макагонова, Н.В. Рогова, О.А. Федосеева. – Пермь: Изд-во Перм. нац. исслед . политехн. ун-та, 2017. – 34 с.
Методические указания составлены в соответствии с рабочей программой дисциплины «Основы системного анализа и математической статистики» по разделу математическая статистика для студентов магистратуры по направлению 08.04.01 «Строительство» Пермского национального исследовательского политехнического университета.
Отражены основы выборочного метода, способы вычисление точечных и интервальных оценок параметров распределения. Рассматриваются элементы теории проверки статистических гипотез, критерии согласия Стьюдента, Фишера, Пирсона, Колмогорова. По каждой теме даны примеры решения задач, в наиболее сложных разделах приведены необходимые теоретические сведения. Предназначено для магистров, бакалавров.
УДК 519.22
© ПНИПУ, 2017
3
Введение
Математическая статистика занимается разработкой методов сбора, обработки и анализа статистических экспериментальных данных для получения обоснованных выводов о параметрах или виде распределения случайных величин.
Основными задачами математической статистики являются
1.Обработка полученных в результате наблюдения (опыта, эксперимента) данных: упорядочить, представить в удобном для обозрения и анализа виде
2.Оценка неизвестных параметров распределения: случайная величина Х имеет функцию распределения определённого вида, зависящую от нескольких параметров, значения которых неизвестны. Требуется на основании опытных данных оценить значения этих параметров.
3.Проверка статистических гипотез: решение вопроса согласования результатов оценивания с опытными данными..
Современная математическая статистика разрабатывает способы определения числа необходимых испытаний до начала исследования (планирование эксперимента) и в ходе исследования (последовательный
анализ) а также |
решает многие другие задачи. Современную |
математическую статистику определяют как науку о принятии решений в условиях неопределенности.
4
1. Основы выборочного метода
Генеральной совокупностью называют совокупность всех возможных объектов данного вида, над которыми проводятся наблюдения.
Выборочной совокупностью или выборкой называют совокупность объектов, отобранных случайным образом из генеральной совокупности.
Наблюдаемые значениях1, х2, …, хk случайной величины Х называются вариантами случайной величины .
Последовательность вариант, записанных в возрастающем порядке,
называется вариационным рядом.
Разность между максимальным и минимальным элементами
выборки называется размахом варьирования. |
|
|
|
|
||
Числа наблюдений n1 , n2 , ..., nk |
значений x1, |
x2 , ..., xk |
называются |
|||
|
k |
|
|
|
|
|
частотами и сумму числа наблюдений, ni n- объемом выборки. |
||||||
|
i 1 |
|
|
|
|
|
Отношения частот к объему |
выборки |
wi |
ni |
|
называются |
|
n |
||||||
|
|
|
|
|||
относительными частотами.
При вычислении относительных частот округление результатов следует проводить таким образом, чтобы общая сумма была равна 1:
k
wi 1
i 1
Числа наблюдений n1, n2 , ..., nk значений x1, x2 , ..., xk называются
k
частотами и ni n - объем выборки.
i 1
|
|
|
|
|
|
5 |
|
|
|
|
Отношения |
частот |
к |
объему выборки wi |
ni |
|
называются |
||||
n |
||||||||||
|
|
|
|
|
|
|
|
|||
относительными частотами. |
|
|||||||||
Отношение |
wi |
ni |
− |
называется плотностью |
частоты, |
|||||
h |
||||||||||
|
|
|
|
|
|
|
|
|
||
отношение |
wi |
|
− плотностью относительной частоты, где h − длина |
|||||||
h |
||||||||||
|
|
|
|
|
|
|
|
|||
частичного интервала, на которые делят весь диапазон наблюдаемых значений.
Соответствие между вариантами и их частотами или относительными частотами называют статистическим распределением случайной величины или статистическим рядом. Статистический ряд обычно записывают в виде таблицы, первая строка которой содержит элементы выборки, а вторая – их частоты.
Если изучаемая случайная величина является непрерывной или число её возможных значений велико, то весь диапазон наблюдаемых значений x1, x2 , ..., xk делят на частичные интервалы, подсчитывают количество ni значений, приходящихся на i-й интервал, и оформляют в виде таблицы, называемой интервальным вариационным рядом
Пример 1.
Данные полученные в результате измерения диаметра валиков после шлифовки занесены в Таблицу 1.
Построить для них полигон и гистограмму частот и относительных частот.
Решение: |
|
|
|
Просматривая результаты наблюдений, |
находим, |
что xmax 6,83, а |
|
xmin 6,68. Объем выборки |
n 200 . |
Размах |
варьирования: |
R 6,83 6,68 0,15
6
Таблица 1
6,75 |
6,77 |
6,77 |
6,73 |
6,76 |
6,74 |
6,70 |
6,75 |
6,71 |
6,72 |
6,77 |
6,79 |
6,71 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6,81 |
6,76 |
6,73 |
6,70 |
6,73 |
6,77 |
6,75 |
6,74 |
6,71 |
6,70 |
6,78 |
6,76 |
6,81 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6,80 |
6,76 |
6,76 |
6,80 |
6,77 |
6,68 |
6,74 |
6,70 |
6,70 |
6,74 |
6,77 |
6,83 |
6,76 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6,77 |
6,71 |
6,74 |
6,74 |
6,80 |
6,74 |
6,77 |
6,75 |
6,74 |
6,75 |
6,77 |
6,72 |
6,74 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6,80 |
6,72 |
6,78 |
6,70 |
6,75 |
6,73 |
6,75 |
6,77 |
6,78 |
6,78 |
6,76 |
6,77 |
6,74 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6,73 |
6,74 |
6,77 |
6,74 |
6,75 |
6,74 |
6,76 |
6,74 |
6,76 |
6,77 |
6,76 |
6,74 |
6,74 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6,76 |
6,74 |
6,72 |
6,80 |
6,76 |
6,78 |
6,73 |
6,70 |
6,76 |
6,77 |
6,75 |
6,76 |
6,76 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6,78 |
6,72 |
6,76 |
6,78 |
6,68 |
6,75 |
6,73 |
6,82 |
6,73 |
6,80 |
6,81 |
6,76 |
6,80 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6,82 |
6,77 |
6,80 |
6,80 |
6,70 |
6,70 |
6,82 |
6,72 |
6,69 |
6,73 |
6,76 |
6,74 |
6,77 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6,76 |
6,72 |
6,76 |
6,78 |
6,78 |
6,73 |
6,76 |
6,80 |
6,76 |
6,72 |
6,76 |
6,76 |
6,70 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6,73 |
6,74 |
6,75 |
6,77 |
6,77 |
6,70 |
6,81 |
6,74 |
6,73 |
6,77 |
6,74 |
6,78 |
6,69 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6,76 |
6,76 |
6,76 |
6,72 |
6,78 |
6,77 |
6,70 |
6,81 |
6,74 |
6,74 |
6,77 |
6,75 |
6,80 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6,77 |
6,77 |
6,81 |
6,75 |
6,72 |
6,76 |
6,77 |
6,78 |
6,73 |
6,76 |
6,76 |
6,76 |
6,77 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6,77 |
6,74 |
6,77 |
6,72 |
6,75 |
6,77 |
6,80 |
6,82 |
6,75 |
6,77 |
6,74 |
6,75 |
6,71 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6,75 |
6,71 |
6,76 |
6,80 |
6,78 |
6,69 |
6,76 |
6,80 |
6,74 |
6,74 |
6.77 |
6,74 |
6,74 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6,73 |
6,74 |
6,74 |
6,76 |
6,82 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Чтобы избежать громоздкости вариационного ряда, полученные данные разбивают на 7 – 11 интервалов. Для определения величины интервала h можно использовать формулу Стерджеса:
|
|
|
|
|
h |
xmax xmin |
, |
|
|||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
1 log n |
|
||||
|
|
|
|
|
|
|
|
2 |
|
|
|
где 1 log2 n − |
количество интервалов, причем log2 n 3,3221 lgn . |
||||||||||
В данном случае |
h |
|
xmax xmin |
|
6,83 6,68 |
0,02 |
|||||
1 |
log2 200 |
1 3,3221 lg200 |
|||||||||
|
|
|
|
|
|||||||
|
7 |
За начало первого |
интервала рекомендуется брать величину |
xнач xmin 0,5h . |
|
В данном случае xнач |
6,67 . |
Промежуточные интервалы получают, прибавляя к концу предыдущего интервала длину частичного интервала h.
Просматривая результаты наблюдений, определяем, сколько значений mi признака попало в i-й интервал. При этом в интервал включают значения случайной величины, большие или равные нижней границе и меньшие верхней границы.
В данном случае интервальный вариационный ряд имеет вид: Таблица 2
|
Частичный |
Частота |
Относительная |
Плотность |
Плотность |
|
относительной |
||||
|
интервал |
частота |
частоты |
||
|
|
частоты |
|||
|
|
|
|
|
|
|
|
|
|
|
|
№ |
xi xi 1 |
ni |
wi ni |
ni / h |
wi / h |
|
|
|
n |
|
|
1 |
6,67 − 6,69 |
2 |
0,01 |
100 |
0,5 |
2 |
6,69 − 6,71 |
15 |
0,075 |
750 |
3,75 |
3 |
6,71 − 6,73 |
17 |
0,085 |
850 |
4,25 |
4 |
6,73 − 6,75 |
44 |
0,22 |
2200 |
11 |
5 |
6,75 − 6,77 |
52 |
0,26 |
2600 |
13 |
6 |
6,77 − 6,79 |
44 |
0,22 |
2200 |
11 |
7 |
6,79 − 6,81 |
14 |
0,07 |
700 |
3,5 |
8 |
6,81 − 6,83 |
11 |
0,055 |
550 |
2,75 |
9 |
6,83 − 6,85 |
1 |
0,005 |
50 |
0,25 |
|
|
200 |
1 |
|
|

8
Рис.1
Рис. 2
Рис. 3

9
Рис.4
Пример 2.
Построить эмпирическую функцию по данному распределению
выборки. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
хi |
|
|
|
|
|
2 |
|
6 |
10 |
|
|
|
|
ni |
|
|
|
|
|
12 |
|
18 |
30 |
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
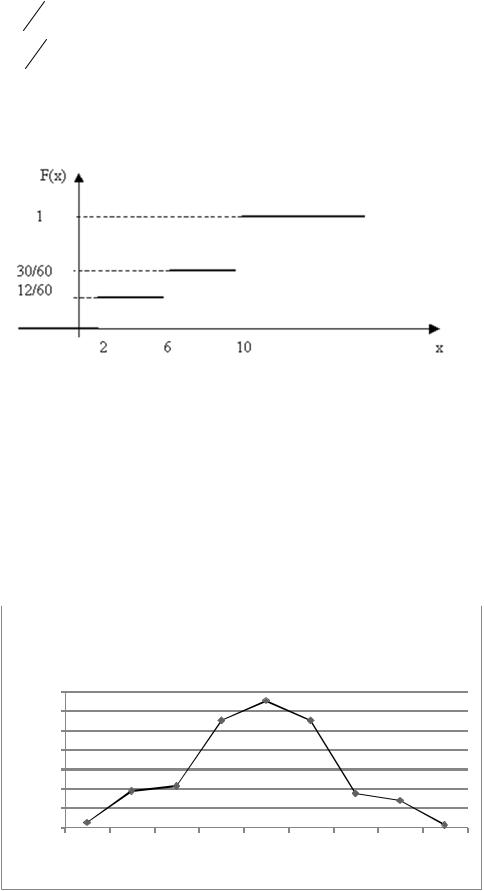
Объем выборки n 12 18 30 60. |
|
|
|
|
|||||||||
Так как xmin 2, то при x 2 |
F*(x) 0 |
60 |
0 (наблюдений меньше 2 нет). |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При 2 x 6 |
F (x) 12 |
60 |
. |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
При 6 x 10 |
F (x) 30 |
60 |
. |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
При x 10 F (x) 1, так как |
xmax 10. |
|
|
|
|
||||||||
Искомая эмпирическая функция имеет вид:
10
|
|
0, |
|
|
x 2, |
|
|
|
60, |
|
|
F |
|
12 |
2 x 6, |
||
|
(x) |
|
, |
6 x 10, |
|
|
|
30 |
60 |
||
|
|
|
|
x 10 |
|
|
|
1, |
|
|
|
График эмпирической функции представлен на рисунке 5: Рис. 5
.
Пример 3.
Построить график выборочной функции плотности распределения по данным примера 1.
Решение:
Значения выборочной функции плотности распределения записаны в последнем столбце таблицы 1, поэтому график будет иметь вид:
Рис.6
