Лабораторная работа № 2- Решение системы линейных уравнений. Разложение вектора по базису

Лабораторная работа №2

Решение системы линейных уравнений. Разложение вектора по базису

Цель работы. Изучение методов решения систем линейных уравнений.

Задание. 1. Разложить вектор по базису , , , где N - номер варианта. Записать выражение в векторной и скалярной формах.

2. Полученную систему линейных уравнений решить методами Гаусса (четные варианты) или Жордано-Гаусса (нечетные варианты). Решение проверить вручную методом Крамера.

Математическое описание. Разложить вектор по базису это значит представить его в виде линейной комбинации , (5)

где - неизвестные коэффициенты. Три вектора образуют базис, если они некомпланарны, то есть их смешанное произведение не равно нулю. Векторное равенство (5) запишем через проекции в виде системы трех линейных уравнений относительно трех неизвестных

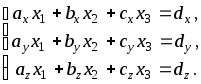(6)

Системой n линейных уравнений относительно n неизвестных называется выражение вида

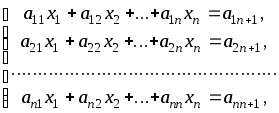, (7)

где -известные коэффициенты, -решение системы, . В матричной форме система может быть представлена в виде

, (8)

где B матрица размера n´n из коэффициентов при неизвестных, С матрица-столбец размера n´1 свободных членов, X - матрица-столбец размера n´1 из неизвестных. Решением системы (7) называется совокупность значений , которые при подстановке в систему обращают все уравнения в тождества. В общем случае система может иметь ноль, одно и бесконечное число решений. Для решения системы линейных уравнений используются прямые методы (Крамера, Жордано-Гаусса, Гаусса, Гаусса с выбором главного элемента и др.) и итерационные методы (простых итерации, Зейделя и др.). Рассмотрим некоторые методы решения системы линейных уравнений.

1. Метод Крамера. Решение системы (7) ищем по формуле

,

где -главный и вспомогательный определители системы. Главный определитель составляется из коэффициентов при неизвестных

.

Вспомогательный определитель системы получается заменой i-го столбца в главном определителе на столбец свободных членов

.

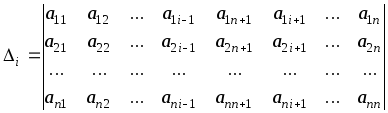2. Метод Жордано-Гаусса. Матрицу B из коэффициентов при неизвестных приводим к единичному виду: все элементы на главной диагонали равны единице, остальные элементы - нулю. Столбец свободных членов показывает при этом решение системы. Алгоритм вычислений следующий.

1). Составляем матрицу A размера n´n+1 из известных коэффициентов a_ij системы (7)

.

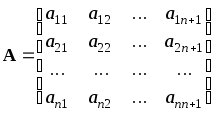2). Начиная с первой строки и первого столбца, выбираем главную строку и столбец. Главный элемент определяется пересечением главной строки и главного столбца.

3). Главную строку делим на главный элемент. При этом главный элемент обращается в единицу.

4). Выбираем текущую строку, которая не должна совпадать с главной. Из текущей строки вычитаем главную, умноженную на элемент, стоящий на пересечении текущей строки и главного столбца.

Рис.3

5). Повторяем п.4 для всех строк. При этом зануляются все элементы главного столбца кроме главного.

6). Пока главная строка не станет последней, повторяем п.2-5.

Алгоритм решения сис-темы методом Жордано-Гаусса приведен на рис.3.

3. Метод Гаусса. Решение системы методом Гаусса проводится в два этапа: прямой ход и обратный ход. При выполнении прямого хода порядок вычислений аналогичен методу Жордано-Гаусса. Однaко после прямого хода метода Гаусса матрица из коэффициентов при неизвестных приводится к треугольному виду. Алгоритм прямого хода метода Гаусса отличается от метода Жордано-Гаусса только организацией цикла по текущим строкам (цикл по j на рис.3): в рассматриваемом методе цикл выполняется от k до n, а не от 1 до n как в предыдущем методе (подумайте, почему?). После выполнения прямого хода система принимает вид:

.

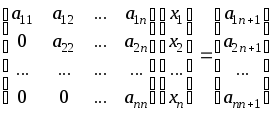При выполнении обратного хода находим значение корней системы: из последней строки определяем n-й корень , из предыдущей (n-1)-й строки - , из i-й - .

4. Метод Гаусса с выбором главного элемента. В общем случае некоторые коэффициенты при неизвестных системы (7) могут принимать нулевые или очень маленькие значения. Если такой элемент оказывается главным и приходится на него делить главную строку, возможен сбой в программе. Для исключения этого недостатка предварительно проводят перестановку строк в исходной системе таким образом, чтобы максимизировать главные элементы системы. После этого система решается методом Гаусса или Жордано-Гаусса.

5. Метод простых итераций (метод Якоби). Для решения системы (7) методом простых итераций представим ее в виде

Задаем начальное приближение корней и определяем первое. Зная k-е приближение, находим k+1

.

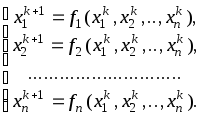Расчет заканчиваем, если k и (k+1) приближения отличаются не более, чем на заданную величину

или .

Итерации сходятся в том случае, если величина модуля каждого диагонального элемента матрицы коэффициентов при неизвестных больше суммы модулей остальных элементов.

6. Метод Зейделя (модифицированный метод простых итераций). Уточненное значение корня (x_i) используется для расчета следущего корня (x_i+1) в том же (k+1)-м приближении

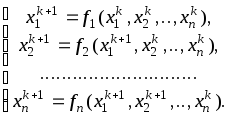
Сходимость метода Зейделя может быть как быстрее, так и медленнее метода простых итераций. Условие окончания расчета аналогично условию предыдущего метода.

Содержание отчета.

1. Название, цель работы и задание.

2. Математическое описание, алгоритм (структограмма) и текст программы.

3. Результаты расчета, проверка, выводы по работе.

- 10 -