Методы преобразования комплексного чертежа

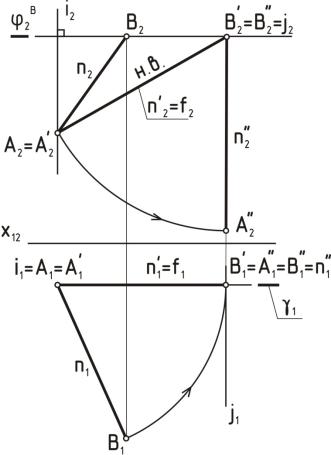
Алгоритм решения задачи на преобразование отрезка прямой общего положения в отрезок уровня

1)Через точку А (А1; А2) проведем ось вращения i π1 (i1=A1). Точка А при вращении останется на месте (А′=А).

2)Переведем отрезок АВ из общего положения в положение линии

уровня [А1 В1] → [А′1 В′1] = f1. Угол поворота точки В определяется условием параллельности [А′1 В′1] оси х12.

3)Из точки В′1 проведем линию связи, перпендикулярную оси х12 и найдем точку пересечения этой линии связи с прямой, проходящими через В2 параллельно х12.

4)Точки А′2 и В′2 будут концами фронтальной проекции отрезка [А′В′], параллельного π2. [А′2 В′2] = f2 – натуральная величина.

Рисунок 19

Преобразование 2. Отрезок уровня [А′В′] преобразовать в проецирующий.

21

Проецирующая прямая на одну плоскость проекций проецируется без искажения и проекция прямой на этой плоскости располагается перпендикулярно оси х12. Следовательно, вращение отрезка [А′В′] в новое положение будем осуществлять относительно оси j π2. В этом случае фронтальные проекции точек отрезка будут перемещаться по окружностям, а горизонтальные проекции точек этого же отрезка будут перемещаться по прямым, параллельным оси х12.

Алгоритм решения задачи на преобразование отрезка уровня в проецирующий

1)Через точку В′ (В′1; В′2) проведем ось вращения j π2 (j2=В′2). Точка В′ при вращении останется на месте (В′=В′′).

2)Переведем отрезок А′В′ из положения линии уровня в проецирующее

положение [А′2 В′2] → [А′′2 В′′2]. Угол поворота точки А′ определяется условием перпендикулярности [А′′2 В′′2] оси х12.

3)Из точки А′′2 проведем линию связи, перпендикулярную оси х12 и найдем точку пересечения этой линии связи с прямой, проходящей через А′1 параллельно х12.

4)Точки А′′2 и В′′2 будут концами фронтальной проекции отрезка [А′′В′′], перпендикулярного π1. А′′1=В′′1 = n′′1 –вырожденная проекция отрезка А′′В′′.

Задача 2. Последовательным вращением вокруг осей, перпендикулярных к плоскостям проекций заданную плоскость α (∆АВС)

общего положения сделать плоскостью уровня (рисунок 20).

Чтобы перевести плоскость из общего положения в уровня, необходимо последовательно выполнить два преобразования. Сначала преобразовать плоскость общего положения в проецирующую, а затем проецирующую плоскость - в плоскость уровня.

Преобразование 1. Плоскость общего положения α (∆АВС) преобразовать в проецирующую плоскость.

Алгоритм решения задачи на преобразование плоскости общего положения в проецирующую

1)В плоскости α(∆АВС) проведем линию уровня – горизонталь h (h1; h2) (h2║x12).

22

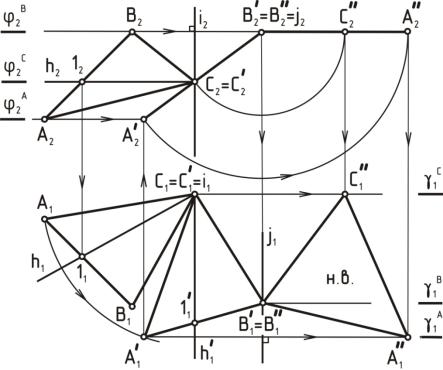
Рисунок 20

2)Переведем плоскость ∆АВС во фронтально проецирующее положение. Для этого горизонталь вращением доводим до положения прямой, перпендикулярной π2 (h′1 х12).

3)На плоскости π1 горизонтальные проекции точек А и В будут перемещаться по окружностям: А1→А′1; В1→В′1 Строим ∆А′1В′1С′1 = ∆АВС по трем сторонам (засечками).

4)На плоскости π2 проекции точек А и В будут перемещаться в плоскостях ϕ2А, ϕ2В, ϕ2С, перпендикулярных оси i2. Находим фронтальные проекции этих точек (А′ и В′) по линиям связи в соответствующих плоскостях.

5)Соединив проекции А′2; В′2; С′2, получаем вырожденную проекцию фронтально-проецирующей плоскости ∆А′В′С′.

Преобразование 2. Проецирующую плоскость α (∆А′В′С′) преобразовать в плоскость уровня.

Плоскость уровня на одну плоскость проекций проецируется в натуральную величину, а на другую в виде прямой, параллельной оси х12.

Алгоритм решения задачи на преобразование проецирующей плоскости в плоскость уровня

1)Через точку В′ (В′1; В′2) проведем ось вращения j π2 (j2=В′2). Точка В′ при вращении останется на месте (В′=В′′).

23

2)При вращении вокруг оси j фронтальные проекции точек А′2 и С′2 перемещаются по окружностям. Угол поворота точек определяется условием параллельности вырожденной проекции плоскости ∆А′′В′′С′′ оси х12 (А′2 → А′′2; С′2 → С′′2).

3)На плоскости π1 проекции точек А′ и С′ будут перемещаться в плоскостях γА, γС, перпендикулярных оси j. Находим горизонтальные проекции этих точек (А′′ и С′′) по линиям связи в соответствующих плоскостях.

4)∆А′′1В′′1С′′1 – натуральная величина плоскости.

3.4.2 Способ вращения вокруг прямой уровня (способ совмещения)

Способ применяется, когда плоскую фигуру требуется совместить с плоскостью уровня, т. е. определить натуральную величину фигуры.

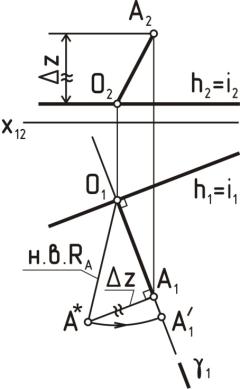
Рассмотрим суть способа на примере вращения точки А вокруг оси i (рисунок 21).

Дано:

точка А – заданный геометрический образ

i– ось вращения (горизонтальная прямая уровня)

1)γ i – плоскость вращения точки А

(γ1 i1)

2)i∩γ=О – центр вращения точки А

(i1∩γ1=О1)

3)[OA] – радиус вращения точки А

([О1 А1], [О2 А2])

4)[О1 А*] – натуральная величина радиуса вращения точки А

Рисунок 21

24

Алгоритм построения нового положения точки способом вращения вокруг линии уровня

1)Точка А, вращаясь вокруг горизонтали, опишет окружность. Плоскость этой окружности γ перпендикулярна оси вращения i и,

следовательно, перпендикулярна плоскости проекций π1. На плоскости π1 горизонтально-проецирующая плоскость γ имеет вырожденную проекцию в виде прямой. Через горизонтальную проекцию точки А (А1) проводим вырожденную проекцию плоскости γ (γ1 i1).

2)Находим точку О (центр вращения точки А), как точку пересечения оси i с плоскостью γ (i1∩γ1=О1; О2 h2 – по линии связи).

3)Соединив проекции О1→А1 иО2→А2 получим проекции радиуса вращения точки А.

4)Чтобы найти новое положение точки А, нужно определить натуральную величину радиуса вращения точки А. Определим ее способом прямоугольного треугольника: за один катет треугольника

примем горизонтальную проекцию радиуса вращения [О1 А1]=R1, другим катетом А1 А* будет разность координат ∆z точек А и О, взятая с плоскости π2. Гипотенуза О1 А* - натуральная величина радиуса вращения точки А.

5)Откладываем [О1 А′1] = [О1 А*].

4 Примеры решения домашних задач

Дан многогранник – пирамида SABC.

4.1 Задача. Определить натуральную величину основания пирамиды

∆ABC (рисунок 22).

Для решения этой задачи необходимо плоскость ∆ABC преобразовать из общего положения, которое она занимает, в положение плоскости уровня. Рационально решать задачу способом вращения вокруг линии уровня.

Алгоритм решения задачи

1)В плоскости ∆АВС через точку А проводим горизонталь h (h1, h2) и принимаем ее за ось вращения.

2)Точка А, лежащая на оси i при вращении остается на месте (А1=А1′). Совместим точку С с горизонтальной плоскость уровня, проходящей через h. Для этого:

а) проводим плоскость вращения точки С - γС h (γС1 h1);

25

Рисунок 22

б) находим центр вращения точки С – точку О (i∩γС=О; i1∩γС1=О1);

в) соединив точку С с центром вращения точкой О, получаем отрезок ОС (О1 С1, О2 С2), который и будет радиусом вращения точки С; г) так как отрезок ОС занимает общее положение, то определяем

натуральную величину радиуса вращения точки С способом прямоугольного треугольника [O1 C′]=[O1 C*]=RC;

д) вращаем точку С вокруг оси i до положения, когда радиус вращения точки С – отрезок [O C] займет положение параллельное π1, т. е. [O C] окажется в плоскости ϕ ║ π1 и на π1 этот отрезок спроецируется без искажения [O1 C′]=[O1 C*].

3)Новое положение точки В можно найти, выполнив построения аналогичные построениям рассмотренным выше для точки С. Однако решение можно упростить, приняв во внимание, то, что точка 1 (точка

26

пересечения горизонтали с [BC]) лежит на оси вращения и, значит, при вращении остается на месте (1=1′).

Точки С, 1, В лежат на одной прямой, следовательно, и точки С′, 1′, В′ будут тоже лежать на одной прямой. Проекцию этой прямой можно провести на плоскости π1 через точки С′1 и 1′1.

Проведя через точку В (В1) плоскость вращения γВ перпендикулярную оси вращения i=h (h1), в пересечении с прямой m(m1) получим точку В′, т. е. новое положение точки В.

Соединив проекции точек А′В′С′ получаем натуральную величину ∆АВС.

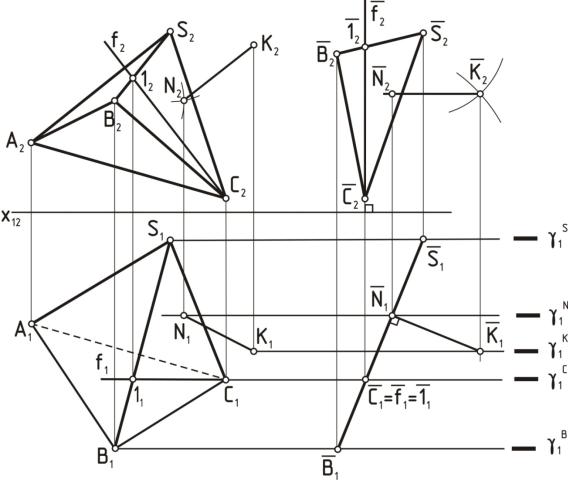
4.2 Задача. Определить натуральную величину угла между смежными гранями пирамиды (рисунок 23).

Двугранный угол (угол между двумя плоскостями) равен линейному углу, полученному при пересечении двугранного плоскостью, перпендикулярной его общему ребру.

Рекомендуется решать данную задачу методом замены плоскостей проекций. Ребро двугранного угла следует преобразовать в проецирующее положение. При этом и каждая грань становится проецирующей.

Найдем величину угла между гранями SCA и SCB. Общее ребро – SC. Чтобы решить данную задачу, нужно последовательно выполнить два преобразования.

Преобразование 1. Ребро SC переведем из общего положения, которое оно занимает, в положение уровня.

Преобразование 2. Переведем отрезок уровня SC в проецирующий.

Алгоритм решения задачи

Преобразование 1.

1)Заменим плоскость проекций π2 на π4 (π2→π4; π4║[SC]) и проведем новую ось координат х14, параллельную [S1 C1].

2)Из горизонтальных проекций А1, В1, С1 и S1 проведем линии связи, перпендикулярные оси х14.

3)Измерив на плоскости проекций π2 высоты точек А, В, С, S, отложим отрезки равные zA, zC, zB, zS по линиям связи от оси х14. Построим проекцию двугранного угла на плоскости π4. Ребро SC ([S4 C4]) стало занимать положение уровня.

27

Рисунок 23

Преобразование 2.

4)Заменим плоскость проекций π1 на π5 (π1→π5; π5 [SC]). Проведем новую ось координат х45, перпендикулярную [S4 C4].

5)Из проекций А4, В4, С4 и S4 проведем линии связи, перпендикулярные оси х45.

6)На этих линиях связи от оси х45 откладываем отрезки :

│А45 А5│=│А14 А1│; │В45 В5│=│В14 В1│ │С45 С5│=│С14 С1│; │S45 S5│=│S14 S1│.

А5С5В5 = ϕ – есть искомый угол.

28

4.3Задача. Определить натуральную величину расстояния от точки

Кдо одной из граней пирамиды (рисунок 24).

Искомое расстояние определяется длиной отрезка перпендикуляра, опущенного из точки на плоскость. Задача решается легче, если плоскость занимает проецирующее положение. Рекомендуется решать задачу способом плоскопараллельного переноса.

Определим расстояние от точки К до грани BSC. Для чего переведем плоскость ∆ BSC из общего положения в проецирующее.

Алгоритм решения задачи

1)В грани BSC проведем линию уровня – фронталь f (f1, f2); f1║x12.

2)Ставим фронталь в горизонтально-проецирующее положение. Для

этого на свободном поле чертежа располагаем f2 x12 и откладываем

[ C2 12] = [C212].

Рисунок 24

29

3)Строим новое положение фронтальной проекции ∆ BSC с помощью

засечек ∆B2 S2 C2 = ∆ B2 S2 C2

|С2В2| = | С2 В2 |; |12В2| = | 12 В2 |; |С2S2| = | С2 S2 |; |12S2| = | 12 S2 |.

4)Строим горизонтальную проекцию ∆B1 S1 C1 по линиям связи. Помня при этом, что горизонтальные проекции точек перемещаются параллельно оси х12.

5)Находим новое положение точки К(К2), также с помощью засечек.

|С2К2| = | С2 К2 |; |S2К2| = | S2 К2 | К1 – по линиям связи.

6)Проведем [ К1 N1] [ B1 S1] – это и будет натуральная величина искомого расстояния.

7)В плоскости π2 находим проекцию [ К2 N2] f2.

8)Строим отрезок [К2N2] с помощью засечек и находим его горизонтальную проекцию по линиям связи.

4.4 Задача. Определить натуральную величину одного из ребер пирамиды (рисунок 25).

Натуральная величина ребра (отрезка) определится, если его перевести в положение прямой уровня.

Найдем натуральную величину ребра AS. Задачу предлагается решать способом вращения вокруг проецирующей оси.

Алгоритм решения задачи

1)Через точку А (А1; А2) проведем ось вращения i π2 (i2=A2). Точка А при вращении останется на месте (А′=А).

2)Переведем отрезок АВ из общего положения в положение линии

уровня [А2 S2] → [А′2 S′2] = h2. Угол поворота точки S определяется условием параллельности [А′2 S′2] оси х12.

3)Из точки S′2 проведем линию связи, перпендикулярную оси х12 и найдем точку пересечения этой линии связи с прямой, проходящей через S1 параллельно х12.

4)Точки А′1 и S′1 будут концами горизонтальной проекции отрезка [А′S′], параллельного π1. [А′1 S′1] = h1 – натуральная величина.

30