Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Саратовский государственный технический университет
имени Гагарина Ю.А.»
Институт прикладных информационных технологий и коммуникаций
Направление «Информатика и вычислительная техника»
Кафедра «Информационно-коммуникационные системы и программная инженерия»
КОНТРОЛЬНАЯ РАБОТА
по дисциплине «Теория вероятностей, математическая статистика и случайные процессы»
Выполнил:
Саратов 2023
Контрольная работа №1
Вариант №2
Задание № 1.
В первой урне
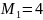белых и
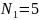черных шаров, а во второй урне
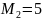белых и
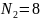черных
шаров. Из первой урны вынимают случайным
образом
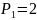шаров, а из второй
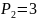шаров. Найти вероятность того, что среди
вынутых шаров:
а) все шары одного цвета;
б) только три белых шара;
в) хотя бы один белый шар.
Решение:
а) все шары одного цвета
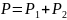
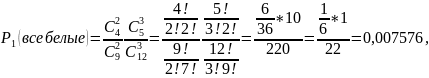
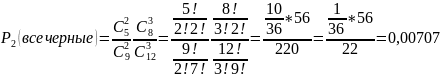
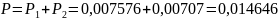
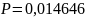
б) только три белых шара;
Возможные варианты вытаскивания 3-х белых шаров
1 {из первой урны 0 белых, из второй 3 белых},
2 {из первой урны 1 белых, из второй 2 белых},
3 {из первой урны 2 белых, из второй 1 белых}.
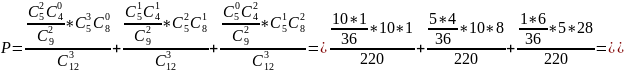
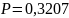
в) хотя бы один белый шар.
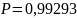
Задание № 2.
В первой урне
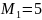белых и
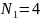черных шаров, а во второй урне
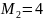белых и
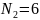черных шаров. Из первой урны случайным
образом вынимают
шаров и опускают во вторую урну. После
этого из второй урны также случайно
вынимают
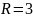шаров. Найти вероятность того, что все
шары, вынутые из второй урны, белые.
Решение:
Рассмотрим события:
H1 {из первой урны во вторую переложили три белых шара},
H2 {из первой урны во вторую переложили три черных шара},
H3 {из первой урны во вторую переложили один белый и два черных шара},
H4 {из первой урны во вторую переложили один черный и два белых шара},
A {из второй урны достали только белые шары}.
Вероятности гипотез равны:
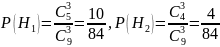
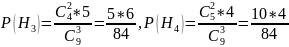
Подставляя найденные вероятности в формулу полной вероятности, получаем
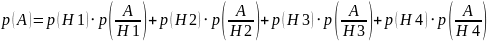
Шаров
во второй урне стало 7 белых и 6 черных
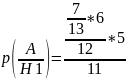
Шаров
во второй урне стало 4 белых и 10черных
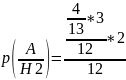
Шаров
во второй урне стало 5 белых и 8черных
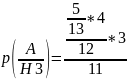
Шаров
во второй урне стало 6 белых и 7черных
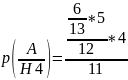
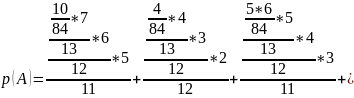
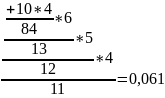
Таким образом, вероятность того, что из второй урны достали только белые шары равна
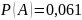
Задание № 3.
В каждом из n=120 независимых испытаний событие A происходит с постоянной вероятностью p=0.5. Найти вероятность того, что в данной серии испытаний событие A наступит:
а) ровно m=85 раз;
б) не менее k=60 и не более m=85 раз;
в) не менее m=85 раз
Решение:
а) При достаточно больших значениях воспользуемся локальной теоремой Лапласа.
,
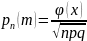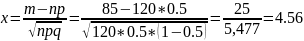
Определим значение функции в найденной точке по таблице
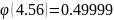
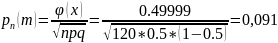
б) не менее k=60 и не более m=85 раз;
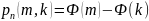
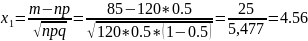
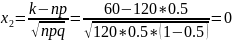
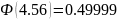
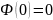
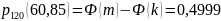
в) не менее m=85 раз
0значает следующее: число появлений события может быть равно либо 85, либо 86, …, либо 120.
m=85 раз
k=120 раз
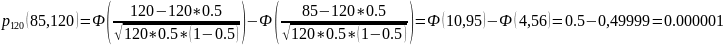
Задание № 4.
В урне M=7 белых и N= 5 черных шаров. Из урны вынимают случайным образом P=4 шаров. Для случайной величины X, равной разности между количеством вынутых белых и черных шаров, требуется:
а) найти закон распределения;
б) построить график функции распределения F(x);
в) найти математическое ожидание M(X) , дисперсию D(X) и среднее квадратическое отклонение (x) D(X) .
Решение:
Поскольку вынимается четыре шара, то возможны следующие элементарные исходы: тогда получаем,
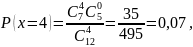
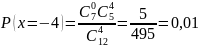
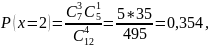
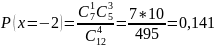
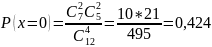
Можно построить ряд распределения
X |
-4 |
-2 |
0 |
2 |
4 |
P |
0,01 |
0,141 |
0,424 |
0,354 |
0,07 |
Функция распределения СВДТ X:
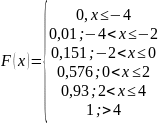
Вычислим математическое ожидание:
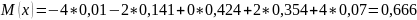
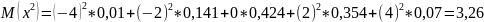
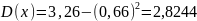
Ответ: М(х)=0,666; D(x)=2,8344
Задание № 5.
Непрерывная случайная величина X задана плотностью распределения
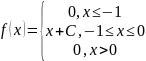
Требуется найти:
а) параметр c;
б) функцию распределения F(x); в) математическое ожидание M (X ) и дисперсию D(X ) .
Решение:
а) Воспользуемся условием нормировки плотности распределения
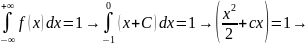
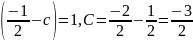
б) Для нахождения функции распределения воспользуемся формулой:
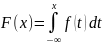
Тогда,
при
x
-1 :
;
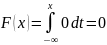при
-1
x 0
:
;
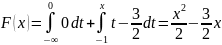при
x
0
: :
;
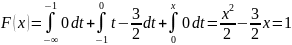Таким образом,
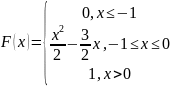
в) Найдем математическое ожидание и дисперсию величины X:
,
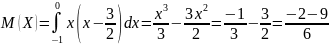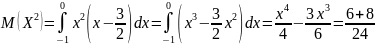
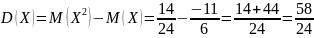
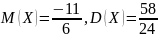
Задание № 6.
Для случайной величины, заданной выборкой, с надежностью и уровнем значимости , на отрезке [a, b] (с числом разбиений отрезка, равным 10 ) и при неизвестном среднем квадратическом отклонении:
а) составить интервальный статистический ряд;
б) построить гистограмму относительных частот;
в) найти точечные и интервальные оценки математического ожидания и среднего квадратического отклонения;
г) проверить гипотезу о нормальном распределении по критерию согласия Пирсона
Решение:
2,53 |
-2,63 |
1,27 |
1,59 |
-0,61 |
-0,67 |
2,92 |
0,63 |
2,88 |
-13,51 |
9,28 |
7,48 |
8,74 |
7,53 |
2,61 |
10,14 |
7,96 |
6,46 |
9,81 |
-10,52 |
-1,16 |
-5,58 |
-3,25 |
-3,86 |
-7,01 |
-5,23 |
-2,26 |
-5,95 |
-1,24 |
-9,25 |
3,34 |
-2,15 |
2,34 |
3,07 |
-0,53 |
0,49 |
4,13 |
1,16 |
3,68 |
-5,36 |
0,48 |
-3,44 |
0,01 |
0,75 |
-3,47 |
-1,82 |
0,04 |
-0,17 |
0,84 |
-4,09 |
4,62 |
1,81 |
3,71 |
5,15 |
-0,14 |
3,95 |
5,89 |
3,15 |
7,13 |
-2,58 |
-4,18 |
-7,73 |
-8,62 |
-6,33 |
-9,16 |
-7,86 |
-6,14 |
-9,82 |
-5,45 |
-2,34 |
4,19 |
0,51 |
3,27 |
3,84 |
-0,38 |
2,17 |
4,35 |
2,25 |
5,68 |
-2,02 |
0,24 |
-3,58 |
-0,35 |
-1,79 |
-3,56 |
-2,71 |
-0,87 |
-2,55 |
0,47 |
-1,64 |
-9,39 |
-14,76 |
-10,03 |
-13,15 |
-12,63 |
-14,23 |
-12,28 |
-12,74 |
-11,16 |
-0,03 |
-4,82 |
-11,52 |
-9,71 |
-6,81 |
-9,53 |
-8,93 |
-6,93 |
-10,60 |
-5,74 |
0,16 |
11,23 |
7,71 |
9,76 |
9,94 |
4,88 |
11,63 |
10,48 |
8,86 |
11,87 |
1,05 |
6,02 |
3,56 |
8,51 |
6,21 |
1,77 |
6,78 |
7,34 |
3,48 |
8,47 |
1,38 |
-8,18 |
-13,82 |
-9,96 |
-11,86 |
-10,75 |
-10,24 |
-8,84 |
-10,93 |
-7,49 |
2,79 |
5,37 |
1,94 |
6,35 |
5,29 |
0,28 |
4,58 |
6,88 |
3,35 |
8,16 |
4,59 |
2,46 |
-3,11 |
0,34 |
1,42 |
-0,76 |
-1,53 |
1,67 |
0,58 |
0,91 |
4,96 |
-1,47 |
-6,68 |
-5,13 |
-4,61 |
-8,25 |
-6,75 |
-2,94 |
-6,29 |
-1,68 |
5,49 |
12,05 |
9,35 |
12,84 |
10,58 |
12,34 |
13,68 |
10,89 |
9,56 |
14,69 |
5,76 |
-3,04 |
-7,19 |
-6,05 |
-5,87 |
-8,47 |
-7,62 |
-4,35 |
-7,28 |
-2,86 |
6,92 |
-0,24 |
-4,52 |
-1,41 |
-2,47 |
-4,06 |
-3,94 |
-1,39 |
-3,38 |
-0,95 |
13,45 |
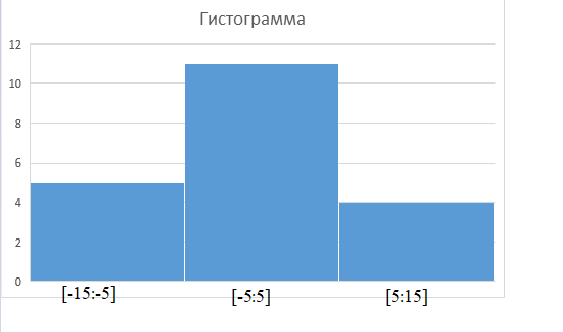
Ширина интервала: h=10
Интервал |
Середина интервала, xцентр |
Частота,fi |
xi·fi |
Накопленная частота |
|x-xср|·fi |
(x-xср)2·fi |
Относительная частота, fi/f |
|
-15 |
-5 |
10 |
53,00 |
530 |
53,00 |
274,54 |
1422,1172 |
0,265 |
-5 |
5 |
0 |
103,00 |
0 |
156,00 |
496,46 |
2392,9372 |
0,515 |
5 |
15 |
10 |
44,00 |
440 |
200,00 |
227,92 |
1180,6256 |
0,22 |
Итого |
|
|
970,00 |
|
998,92 |
4995,68 |
1 |
|
Средняя взвешенная (выборочная средняя) – точечное математическое ожидание.
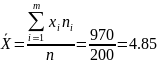
Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего)
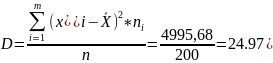
Среднее квадратическое отклонение.
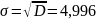
Доверительный интервал для генерального среднего
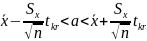
Определяем значение tkp по таблице распределения Стьюдента.
По
таблице Стьюдента находим:
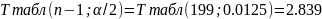Стандартная
ошибка выборки для среднего:
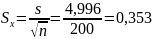
Стандартная ошибка среднего указывает, на сколько среднее выборки 4,85 отличается от среднего генеральной совокупности. Предельная ошибка выборки:
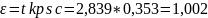
Доверительный интервал:
(
–
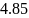1,002;
+
1.002) = (3,848;5,852)
С вероятностью 0,99 можно утверждать, что среднее значение при выборке большего объема не выйдет за пределы найденного интервала
Доверительный интервал для среднеквадратического отклонения.
S*(1-q) <σ <S*(1+q)
Найдем доверительный интервал для среднеквадратического отклонения с надежностью γ = 0.99 и объему выборки n = 200.
По таблице q=q (γ; n) определяем параметр q (0.99;200) = 0
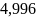(1-0) < σ <
(1+0)
< σ <
Таким образом, интервал ( ; ) покрывает параметр σ с надежностью
γ = 0.99
Проверим гипотезу о том, что Х распределено по нормальному закону с помощью критерия согласия Пирсона.
где pi — вероятность попадания в i-й интервал случайной величины, распределенной по гипотетическому закону
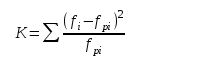
Для вычисления вероятностей pi применим формулу и таблицу функции Лапласа
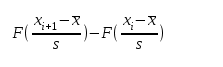
Где
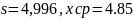
Теоретическая (ожидаемая) частота равна fi = fpi, где f = 200
Вероятность попадания в i-й интервал: pi = Ф(x2) - Ф(x1)
Определим границу критической области. Так как статистика Пирсона измеряет разницу между эмпирическим и теоретическим распределениями, то чем больше ее наблюдаемое значение Kнабл, тем сильнее довод против основной гипотезы.
Поэтому критическая область для этой статистики всегда правосторонняя: [Kkp; +∞).
Её границу Kkp = χ2(k-r-1; α) находим по таблицам распределения χ2 и заданным значениям s, k (число интервалов), r=2 (параметры xcp и s оценены по выборке).
Kkp = χ2(3-2-1;0.01) = 249.4451; Kнабл = 0.24
Наблюдаемое значение статистики Пирсона не попадает в критическую область: Кнабл <Kkp, поэтому нет оснований отвергать основную гипотезу.
Справедливо предположение о том, что данные выборки имеют нормальное распределение.
Выводы:
Каждое значение ряда отличается от среднего значения в среднем на 6.431.
Среднее значение примерно равно моде и медиане, что свидетельствует о нормальном распределении выборки.
Проверка гипотезы по критерию согласия Пирсона показала, что нет оснований отвергать гипотезу о нормальном законе распределения.
Работу выполнил: Никитин Константин Петрович
Дата: 12.06.2023г.
Подпись_______