
методичка из инета по мн-вам
.pdf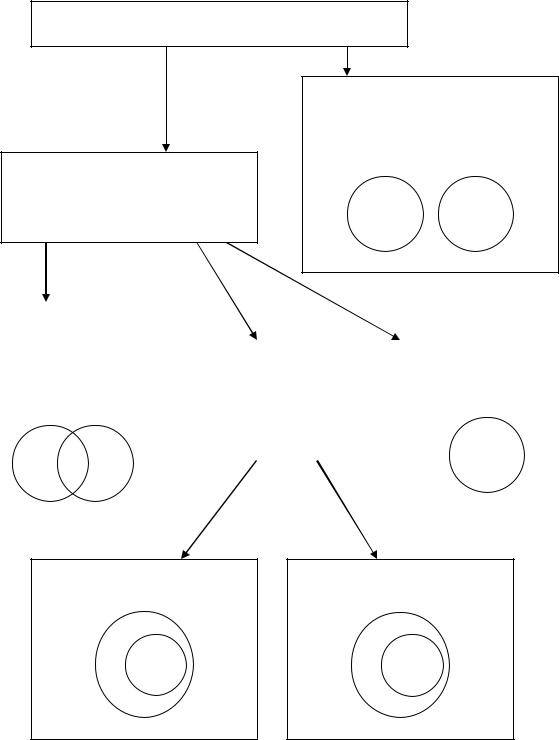
Отношения между множествами А и В
Множества А и В находятся в отношении
пересечения
Множества А и В находятся в отношении
непересечения
АВ
Множества А и В |
|
|
|
|
|
|
|
Множества А и В |
|||
находятся в |
|
|
|
||
|
Множества А и В |
|
|||
|
|
находятся в |
|||
отношении |
|
|
|||
|
находятся в |
|
отношении |
||
пересечения общего |
|
|
|||
|
отношении |
|
равенства |
||
положения |
|
|
|||
|
включения |
|
|
||
|
|
|
|
|
|
А |
В |
|
|
|
А=В |
|
|
|
|||
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Множество А включает |
Множество В включает |
в себя множество В |
в себя множество А |
АВ
ВА
11
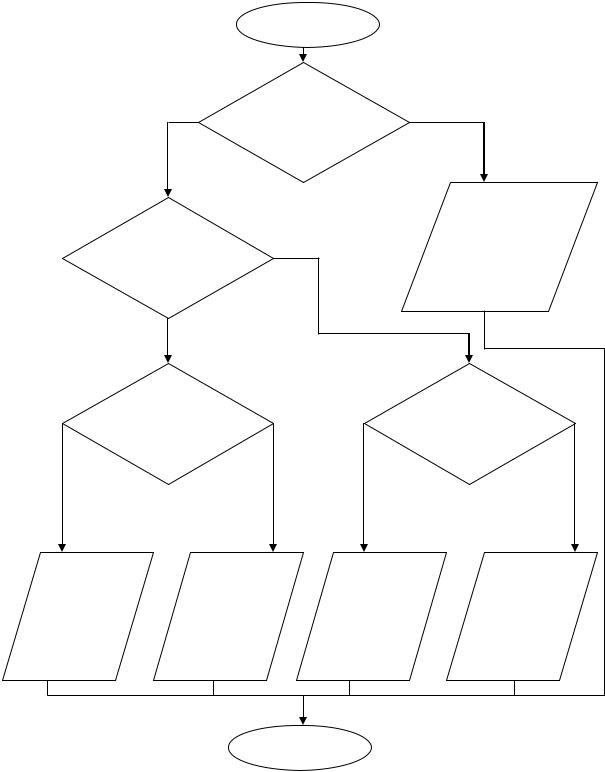
Алгоритм определения вида отношения между двумя |
||||||
|
множествами А и В |
|
|
|
||
|
|
Начало |
|
|
|
|
|
|
У |
|
|
|
|
|
ДА |
множеств А |
НЕТ |
|
||
|
|
и В есть общие |
|
|
|
|
|
|
элементы? |
|
|
|
|
|
|
|
|
|
Множества |
|
|
Все |
|
|
|
А и В |
|
|
|
|
|
находятся |
||
элементы |
НЕТ |
|
|
|||
|
|
в |
|
|||
множества В |
|
|
|
|
||
|
|
|
отношении |
|||
принадлежат |
|
|
|
|||
|
|
непересечения |
||||
|
А? |
|
|
|||
|
|
|
|
|
|
|
ДА |
|
|
|
|
|
|
|
Все |
|
|
|
Все |
|
элементы |
|
|
элементы |
|
||
множества А |
|
|
множества А |
|
||
принадлежат |
|
ДА |
принадлежат |
|
||
ДА |
В? |
НЕТ |
|
В? |
|
|
|
|
НЕТ |
||||
|
|
|
|
|
|
|
Множества |
Множество |
Множество |
Множества |
|||
А и В |
А включает |
В включает |
А и В |
|||
находятся |
в себя |
в себя |
|
находятся |
||
в |
множество |
множество |
в общем |
|||
отношении |
В |
А |
|
положении |
||
|
пересечения |
|||||
равенства |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Конец |
|
|
|
|
|
|
12 |
|
|
|
|

2. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
Над множествами, как и над многими другими математическими объектами, можно совершать различные операции. В результате операций из исходных множеств получаются новые. Операции бывают бинарные (которые выполняются над двумя множествами) и унарные (которые выполняются над одним множеством). К бинарным операциям относятся: пересечение, объединение, вычитание, симметрическая разность, декартово или прямое произведение и др. К унарным операциям можно отнести: нахождение мощности множества, разбиение множества и др. Рассмотрим основные из них.
2.1. Пересечением множеств А и В называется множество, содержащее все элементы, которые принадлежат множеству А и множеству В одновременно.
A B {x | x A и x B}.
На диаграммах Эйлера — Венна результат операций пересечения множеств изображается как общая часть геометрических фигур, представляющих эти множества.
А
А |
B |
В |
А |
А=В |
|
||||
В |
|
А |
В |
|
|
|
|
||
А В= |
|
|
|
|
Процесс нахождения множества |
А В называется |
операцией |
||
пересечения.
Операцию пересечения можно выполнить над любыми множествами, вне зависимости от того, в каких отношениях находятся сами множества, т. е. пересечение любых множеств всегда существует и единственно.
Рассмотрим пример.
A – множество однозначных натуральных чисел, кратных 3.
B = {1, 3, 5, 9, 11}
А В={3, 9}
2.2. Объединением множеств А и В называется множество, содержащее все элементы, которые принадлежат множеству А или множеству В.
13

A B {x | x A или x B}.
На диаграммах Эйлера —Венна результат операций объединения множеств изображается как часть плоскости, занимаемая геометрическими фигурами, представляющими эти множества.
А |
|
|
|
А |
В |
|
|
В |
В |
А |
А=В |
|
|
|
|
|
А |
В |
|
Процесс нахождения |
множества А В называется |
операцией |
|
объединения.
Операцию объединения можно выполнить над любыми множествами, вне зависимости от того, в каких отношениях находятся сами множества, т. е. объединение любых множеств всегда существует и единственно.
Рассмотрим пример.
A – множество однозначных натуральных чисел, кратных 3.
B = {1, 3, 5, 9, 11} А В={1, 3, 5, 6, 9, 11}
2.3. Разностью множеств А и В называется множество, содержащее все элементы, которые принадлежат множеству А и не принадлежат множеству В.
A \ B {x | x A и x B}.
На диаграммах Эйлера — Венна результат операций вычитания множества В из множества А изображается как часть геометрической фигуры, представляющей множество А после удаления фигуры, изображающей множество В.
А
АВ
В |
А |
А=В |
В |
|
|
А |
В |
|
Процесс нахождения множества А\В |
называется |
операцией |
вычитания. |
|
|
14

Операцию вычитания можно выполнить над любыми множествами, вне зависимости от того, в каких отношениях находятся сами множества, т. е. разность любых множеств всегда существует и единственна.
Пример 1.
A – множество однозначных натуральных чисел, кратных 3.
B = {1, 3, 5, 9, 11} А\В={6}, В\А={1, 5, 11},
Пример 2.
X={x, x R, x<4}, Y= {x, x N, x<4}. Найдем Х\Y. Изобразим их на координатной прямой.
Х |
|
|
|
|
Y |
4 |
|
|
1 |
2 |
3 |
|
|
|
Х \ Y |
|
|
1 |
2 |
3 |
4 |
|
|
В этом случае Х\Y записывается как объединение непересекающихся множеств Х\Y=(-∞, 1) (1, 2) (2, 3) (3, 4)
Если B A , то дополнением множества В до множества А называется множество, содержащее все элементы множества А, которые не принадлежат множеству В.
|
|
|
|
B |
/ |
{x | x |
A и x B}. |
|
|
|
|
A |
|||
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим пример. |
|
|
|
|
A |
|
= {1, 3, 5, 9, 11, |
|
13, 17, |
37}, B = {1, 3, 5, 9, 11}, |
||
B |
/ |
|
{13, |
17, 37}. |
|
|
|
A |
|
|
|
||||
|
|
|
|
|
|
||
2.4. Симметрическая разность двух множеств — это множество, включающее все элементы исходных множеств, не принадлежащие одновременно обоим исходным множествам. Другими словами, если есть два множества 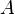 и
и  , их симметрическая разность есть объединение элементов
, их симметрическая разность есть объединение элементов  , не входящих в
, не входящих в 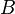 , с элементами
, с элементами 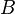 , не входящими в
, не входящими в  . На письме для обозначения симметрической разности множеств
. На письме для обозначения симметрической разности множеств 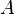 и
и 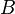 используется обозначение
используется обозначение
Симметрическую разность можно ввести двумя способами:
симметрическая разность двух заданных множеств  и
и 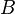 — это такое множество
— это такое множество 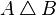 , куда входят все те элементы первого множества, которые не входят во второе множество, а, также те
, куда входят все те элементы первого множества, которые не входят во второе множество, а, также те
15

элементы второго множества, которые не входят в первое множество:
симметрическая разность двух заданных множеств  и
и  — это такое множество
— это такое множество  , куда входят все те элементы обоих множеств, которые не являются общими для двух заданных множеств.
, куда входят все те элементы обоих множеств, которые не являются общими для двух заданных множеств.
Понятие симметрической разности можно обобщить на число множеств, большее двух.
Пример. А={1, 2, 3, 4}, B={3, 4, 5, 6}. A∆B= {1, 2, 5, 6} A\B={1, 2}, B\A={5, 6}, A∆B=(A\B) (B\A)={1, 2, 5, 6}.
A B={1, 2, 3, 4, 5, 6}, A∩B={3, 4}, A∆B=(A B)\(A∩B)={1, 2, 5, 6}
Приоритет выполнения операций
Сначала выполняются операции дополнения и пересечения, а затем объединения и разности, которые имеют одинаковый приоритет
ивыполняются в порядке записи. Симметрическая разность рассматривается как комбинация операций объединения, вычитания
ипересечения. Последовательность выполнения операций может быть изменена скобками.
2.5.Декартовым произведением множеств А и В называется множество всех пар, первая компонента которых принадлежит множеству А, а вторая компонента принадлежит множеству В.
A B {(x; y) | x A и y B}
Если множества А и В конечны, то декартово произведение этих множеств можно изобразить при помощи графа и таблицы, а декартово произведение любых числовых множеств удобно изобразить на координатной плоскости.
Например, декартово произведение множеств А={3, 5, 7} и B={2, 4} можно представить следующим образом:
|
В |
1 |
3 |
А |
|
||
|
|
|
|
-1 |
|
(-1,1) |
(-1,3) |
|
|
|
|
1 |
|
(1,1) |
(1,3) |
|
|
|
|
3 |
|
(3,1) |
(3,3) |
|
|
|
|
А |
В |
|
-1 |
|
|
1 |
1 |
|
|
|
|
3 |
3 |
-3 -2 -1 0 1 2 3 x |
|
||
|
|
16

На рисунках изображены декартовы произведения множеств А и В:
1)А = {–3 –2, –1}, B= (–2; +∞); рис. 1.
2)A = {1, 2}, B = {–1, 0, 1, 2, 3}; рис. 2.
3)A = [–2; 3), B = {1, 2, 3}; рис. 3.
4)A = (-∞; 4], B = [-2; 2]; рис. 4.
5)A = [-1; 3), B = (-2; 3] рис. 5.
6)A = [–2; 3], B = [–2, 3]. рис. 6.
-3 -2 -1 0 1 2 3 x |
-3 -2 -1 0 1 2 3 x |
-3 -2 -1 0 1 2 3 x
рис.1 |
рис.2 |
рис.3 |
-3 -2 -1 0 1 2 3 x
-3 -2 -1 0 1 2 3 x
-3 -2 -1 0 1 2 3 x
рис.4. |
рис.5 |
рис.6 |
Разбиение множества на классы. Классификация
Классификация – это действие распределения объектов по классам на основании сходств внутри класса и их отличия от других объектов. Классификация широко применяется в математике.
Считают, что множество Х разбито на классы Х1, Х2, …, Хn, …, если:
1)подмножества Х1, Х2, …, Хn, … попарно не пересекаются;
2)объединение подмножеств Х1, Х2, …, Хn, … совпадает с множеством Х.
Например: а) Множество треугольников разбито на три класса: остроугольные, прямоугольные и тупоугольные. Действительно, выделенные подмножества попарно не пересекаются, а их объединение совпадает с множеством всех треугольников.
b) Из множества треугольников выделили подмножества равнобедренных, равносторонних и разносторонних треугольников.
17
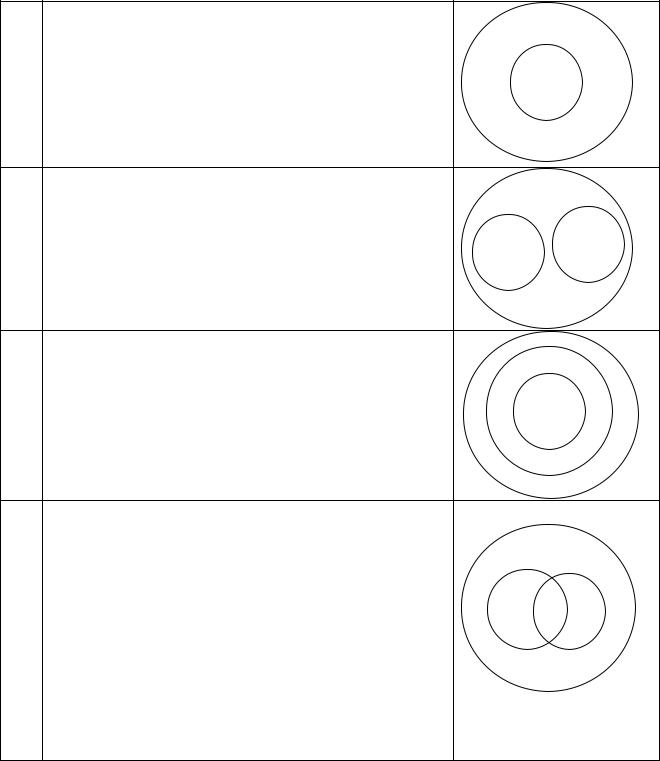
Так как множества равнобедренных и равносторонних треугольников пересекаются, значит, не выполнено первое условие классификации, и разбиения множества треугольников на классы мы не получили.
Разбить множества на два класса можно выделив собственное подмножество. Такое разбиение называется дихотомическим.
Пример 1
Пример 2
Пример 3
Пример 4
Дихотомическое разбиение на классы
А – множество натуральных чисел.
В – множество четных натуральных чисел.
Выделив из множества А подмножество В, мы А В произвели разбиение множества А на два класса:
В и А\В (множество нечетных натуральных чисел)
A=N |
|
|
|
|
|
|
|
|
|
B={x, x N, x<5} |
|
|
|
А |
|
|
|||
C={x, x N, x>10} |
|
|
|
|
|
||||
|
|
|
1 |
|
2 |
||||
Произошло разбиение на три класса: |
|
|
|
|
|||||
|
|
В |
|
|
С |
||||
1 |
класс: В={x, x N, x<5} |
|
|
|
|
||||
2 |
класс: С={x, x N, x>10} |
|
|
|
|
3 |
|
|
|
3 |
класс: А\(В С) ={x, x N, 5 x 10} |
|
|
|
|
|
|
|
|
A=N |
|
|
|
|
|
|
|
|
|
B={x, x N, x<30} |
|
|
|
|
|
|
|
||
C={x, x N, x<10} |
А |
В |
|
|
|
|
|||
Произошло разбиение на три класса: |
С |
1 |
|
||||||
|
|
|
|
||||||
1 |
класс: C={x, x N, x<10} |
|
|
|
|
|
|
2 3 |
|
2 |
класс: B\С={x, x N, 10 x<30} |
|
|
|
|
|
|
||
3 |
класс: А\В ={x, x N, x 30} |
|
|
|
|
|
|
|
|
В – множество натуральных чисел кратных 2. |
|
|
|
|
|
|
|
||
С – множество натуральных чисел кратных 3. |
|
|
|
|
|
|
|
||
Произошло разбиение на четыре класса. |
|
|
|
|
А |
|
|
||
1 |
класс: В С |
– множество натуральных чисел |
|
|
|
|
|
|
|
кратных 6. |
|
|
В |
|
1 |
|
С |
||
2 |
класс: В\С – множество натуральных чисел |
|
|
|
|||||
|
|
|
|
|
|||||
|
|
|
2 |
|
|
3 |
|||
кратных 2, но не кратных 3. |
|
|
|
|
|
||||
3 |
класс: С\В |
– множество натуральных чисел |
|
|
|
|
4 |
|
|
кратных 3, но не кратных 2. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
4 |
класс: А\(В С) – множество натуральных |
|
|
|
|
|
|
|
|
чисел не кратных ни 2, ни 3. |
|
|
|
|
|
|
|
||
18
3. СВОЙСТВА ОПЕРАЦИЙ НАД МНОЖЕСТВАМИ
Свойства |
Коммутативность |
Ассоциативность |
|
Операции |
|||
|
|
||
|
|
|
|
|
1 |
3 |
|
|
A B B A |
A (B C) |
|
Пересечение |
|
( A B) C |
|
2 |
4 |
|
Объединение |
A B B A |
A (B C) |
|
|
|||
|
( A B) C |
||
|
|
||
|
|
|
|
Вычитание |
Не обладает |
Не обладает |
|
|
|
|
|
Симметрическая |
5 |
6 |
|
разность |
|||
А∆В=В∆А |
А∆(В∆С)=(А∆В)∆С |
||
|
|||
|
|
|
|
|
|
Строго говоря, |
|
|
|
тождество |
|
|
|
ассоциативности |
|
|
|
не имеет места, но в |
|
|
|
силу существования |
|
Декартово |
Не обладает |
естественного взаимно |
|
произведение |
однозначного |
||
|
|||
|
|
соответствия между |
|
|
|
множествами |
|
|
|
и |
|
|
|
этим |
|
|
|
различием можно |
|
|
|
зачастую пренебречь |
7 Дистрибутивность объединения множеств относительно пересечения A (B C) ( A B) ( A C) .
8 Дистрибутивность пересечения множеств относительно объединения A (B C) ( A B) ( A C) .
19
9 Дистрибутивность пересечения множеств относительно разности A (B \ C) ( A B) \ ( A C) .
10Дистрибутивность пересечения множеств относительно симметрической разности: 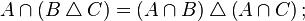
11Дистрибутивность декартова произведения относительно
объединения A (B C) (A B) (A C) .
12 Дистрибутивность декартова произведения относительно пересечения A (B C) (A B) (A C) .
13 Дистрибутивность
симметрической разности A
декартова
(B C)
произведения
(A B) (A
относительно
C) .
14 Дистрибутивность
вычитания множеств |
A |
декартова произведения
(B \ C) (A B) \ (A C)
относительно
.
|
Пересе- |
Объеди- |
|
Симметри- |
Декартово |
|
Вычитание |
ческая |
произведе- |
||
|
чение |
нение |
|||
|
|
разность |
ние |
||
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
20 |
|
15 |
16 |
17 |
19 |
|
А и |
А = |
А = |
А\ = А |
А∆ =А |
А = |
|
|
А |
18 |
|
|
|
|
|
\А = |
|
|
|
|
|
|
|
|
А и А |
21 |
22 |
23 |
24 |
|
А А=А |
А А = |
А \ А = |
А∆А= |
|
|
|
|
||||
|
|
=А |
|
|
|
|
|
|
|
|
|
А и А’ |
25 |
26 |
27 |
28 |
|
А А’ = |
A A’ = |
A \ A’ = A |
A ∆ A’ = |
|
|
|
|
||||
|
|
=U |
|
=U |
|
|
|
|
|
|
|
Законы |
29 |
30 |
|
|
|
Де |
(A B)’= |
(A B)’ |
|
|
|
Моргана |
A’ B’ |
= A’ B’ |
|
|
|
|
|
|
|
|
|
20
