
lec04
.pdf
Часть 3.
Интервалы булевой функции и покрытия.

Носитель элементарной конъюнкции K ранга r называется
интервалом NK ранга r.
Интервал NK ранга r содержит n-r векторов (вершин в Bn). | NK |= 2n-r. Т.е. все те вектора на r местах на которых сомножители в элементарной конъюнкции будут равны 1.
K = σ1 |
σ2 |
… σ |
|
|
|
1 |
2 |
|
N = … , |
|
|
, … |
|
|
|
1 |
|
, … |
||
K |
1 |
|
|
||
|
|
||||
12
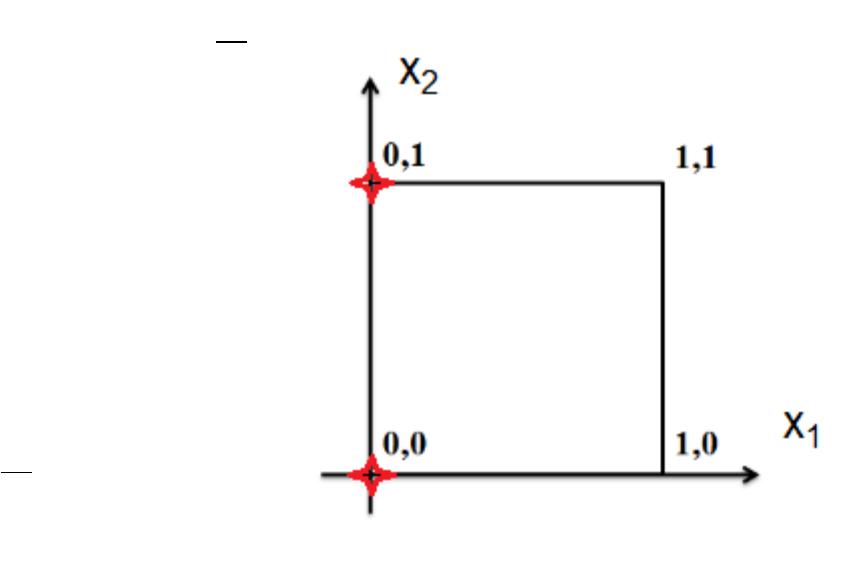
Пример. 4.4. БФ f (x1,x2).
а) Найти носитель для конъюнкта K = 1 2
n=2, r=2.
x1 = 1, x2 = 0.
NK = { (1,0) }. |NK|=2n-r=22-2=1.
б) если взять f (x1,x2,x3) для той же K.
n=3, r=2.
При x1 = 1, x2 = 0: x3 - любое.
NK = { (1,0,0); (1,0,1)}. |NK|=23-2=2.
в) если взять f (x1, x2). K = 1.
при x1 = 0: x2 – любое, т.е. (x2 = 0 или x2 = 1).
NK = { (0,0); (0,1) }. |NK|=22-1 =2.
Что образует NK в B3 ?
13
Утверждение 4.1. Для n переменных (x1,x2, … xi, … xn) интервал для конъюнкции K ранга r - грань в Bn, размерность которой равна:
n – r, (количество вершин в интервале).
Совокупность интервалов N1, N2, … Ni, … NS образует покрытие для функции , если выполняется условие:
Nf = N1 N2 … Ni … NS
в частности отсюда вытекает, что целиком содержится Ni Nf.
Интервал Ni называется допустимым, если Ni Nf.
14
Теорема о покрытии БФ интервалами конъюнктов.
Теорема 4.1.
Если D = K1 K2 … KS есть некоторая ДНФ для булевой функции, то соответствующие интервалы для конъюнктов
1, 2 , … ,
образуют покрытие для функции .
Доказательство.
Следует из определения покрытия.
15
Из теоремы 4.1 следует:
Утверждение 4.2.
Nf g = Nf Ng
т.е. фактически наблюдаем связь между операциями над носителями с операциями для функций.
Пусть Вn – вершина булева куба, Вn в точке, где
g( ) = 1 ( ) = 1 или g( ) = 1 Nf или Ng
Nf Ng. Показано, что левая часть лежит в правой
Nf g Nf Ng
Аналогично справа налево показывается и обратное включение:
Nf Ng Nf g Nf g = Nf Ng
16

Часть 4.
Максимальные интервалы и сокращённая ДНФ.
Рассмотрим (x1,x2, … xn) представленную суммой ДНФ. Минимизируем ее ранг. Имеет смысл рассматривать покрытие
Nf = 1 2 …
которое будет соответствовать
Dmin = 1 2 …
Для булевой функции интервал NK называется максимальным, если:
NK Nf ; NK': NK NK' Nf
(т.е. другого допустимого интервала целиком содержащего в себе исходный).
Логическая сумма всех конъюнкций, отвечающей максимальным интервалам NK для функции называется сокращенной ДНФ - DC.
18
Теорема о равенстве БФ ее сокращенной ДНФ.
Теорема 4.2.
Имеет место = DC.
Доказательство.
Совокупность всех интервалов покрывает ДНФ, что очевидно.
19
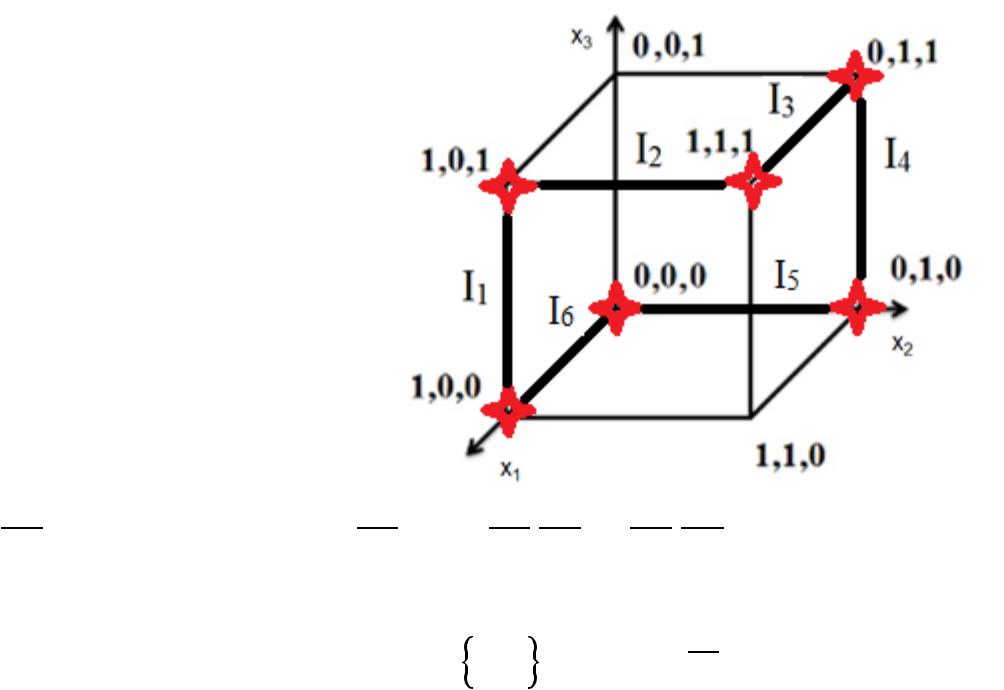
Пример 4.5а.
= (1011 1101); n = 3.
Найти сокращенную ДНФ. DC = ?
Решение геометрическое.
Находим max интервалы.
Nf = I1 I3 I5 I2 I4 I6
n = 3, |NK|=2(=2n-r). n – r = 1. r = 2.
DC = 1 2 1 3 2 3 1 2 1 3 2 3
DC – СокрДНФ, т.к. Ii грани, содержащей интервал Ii и общей для других вершин (например, интервал (ребро) I1 = 101100 ↔ K1 = 1 2).
