
lec08
.pdf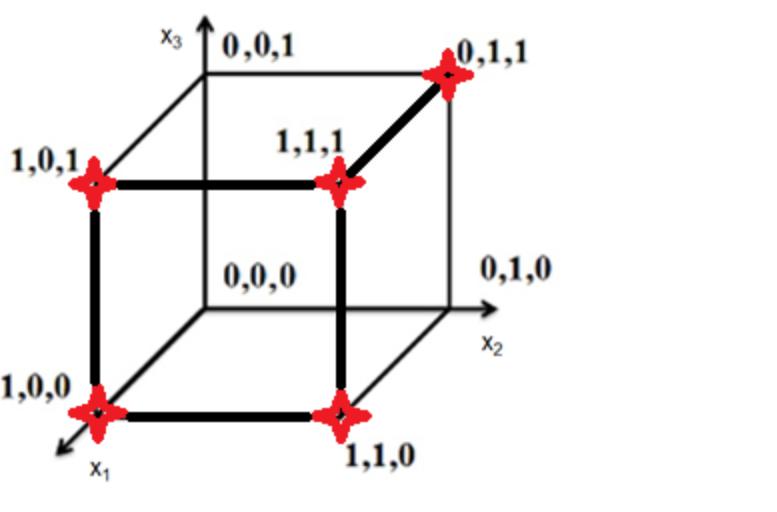
Пример 8.5. Монотонность в B3.
б) f1 = (0001 1111);
макс интервалы:
DC = |
x |
x x |
3 |
|
1 ?2 |
||
DC |
|
Нет. |
D |
|
? |
C |
Итог: f2 – монотонна
x1 |
x2 |
x3 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
11
Теорема 8.1. Множество всех монотонных функций является замкнутым классом и обозначает M. [M] = M.
Доказательство:
Рассмотрим суперпозицию любых БФ из M, то есть функцию
(x1, … xn) = 0( 1(x1, … xn), …, m(x1, … xn)).
Подставим в суперпозицию любую пару ( , ):
= (x1, x2, … xn), = (x1, x2, … xn); , M; . Получим
( ) = 0( 1( ), …, m( )) = 0(γ),( ) = 0( 1( ), …, m( )) = 0(δ),
где γ, δ Вn. Т.к. и 1(x1, … xn), …, m(x1, … xn) – монотонны, то γ δ. Т.к. 0(x1, … xn) также монотонна, то 0(γ) 0(δ).
Т.е. ( ) ( ) М замкнут.
12

Часть 3.
Самодвойственные функции.

Самодвойственные БФ.
(x1, x2, … xn) – произвольная булева функция.
Напоминание: двойственной к функции называется БФ:
(x1, x2, … xi, … xn) ( 1, 2, … , … ).
БФ (x1, x2, … xn) называется самодвойственной, если *= :
(x1, x2, … xn) = ( 1, 2, … )
или
(x1, x2, … xn) = ( 1, 2, … ).
14
Утверждение 8.2.
Если булева функция (x1,x2,…xn) самодвойственна, то – самодвойственна.
Утверждение 8.3.
Функция (x1,x2,…xn) самодвойственна на всяких двух противоположных наборах ( , ) она принимает разные значения.
( , ) при ρ( , )=n:
( ) ≠ ( )
15
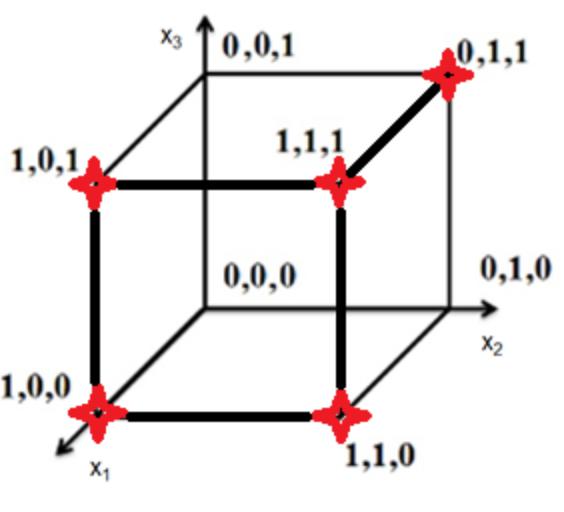
Пример 8.6. Самодвойственность в B3.
а) f1 = (0001 1111); (из примера 8.5б)
Какое число единичных вершин в B3 является необходимым условием
самодвойственности |N?| = 4
f
а в Bn |?Nf| = 2n-1
Итог: f1 – не самодвойственна
16

Пример 8.6. Самодвойственность в B3.
б) f2 = (0111 0001);
Необходимое условие числа единичных Да? вершин в B3 выполняется
, при ρ( , )=3: f( ) ≠ f( ) |
Нет |
|
? |
=(001), =(110), (ρ( , )=3): |
|
f( ) = f (001) = 1 = f (110) = f ( ). |
|
Итог: f2 – не самодвойственна
x1 |
x2 |
x3 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
17
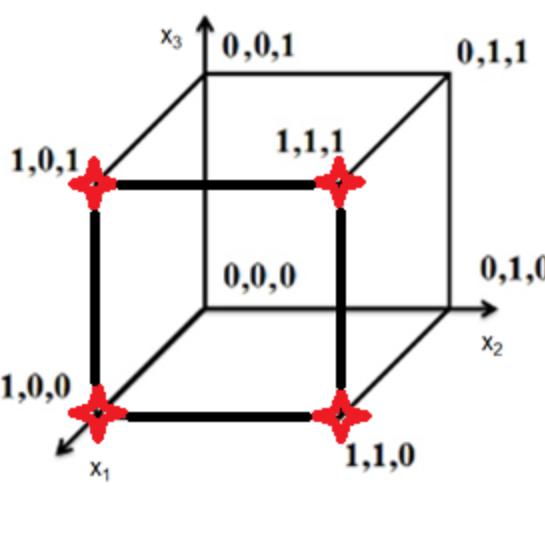
Пример 8.6. Самодвойственность в B3.
в) f2 = (0000 1111);
Необходимое условие числа единичных
вершин в B3 выполняется |
? |
|
Да |
, при ρ( , )=3: f( ) ≠ f( ) |
? |
|
Да |
Итог: f3 – самодвойственна |
|
Т.е. во всех парах противоположных вершин задана только 1 единичная вершина !
18
Утверждение 8.4. Число различных самодвойственных БФ, зависящих от n переменных, равно 22n 1.
Доказательство: Рассмотрим самодвойственную функцию n аргументов, заданную ТИ. Если на первом наборе она принимает значение a, то, согласно свойству самодвойственной функции, на последнем наборе (противоположном первому) она принимает значение a. То же можно сказать о втором и предпоследнем наборах, и так далее. Таким образом, самодвойственная функция полностью определяется верхней половиной своего столбца значений ТИ, то есть булевым вектором длины 2n/2=2n-1.
Согласно теореме о числе 22n для (x1, x2, … xn) БФ однозначно задается вектором длины 2n. Если БФ однозначно задается вектором длины 2n-1, то
число таких БФ = 22n 1.
Пример 8.7.
Из всех 16 булевых функций (x1,x2) 4 функции (22) принадлежат классу S: тождественные функции x1 и x2 и их инверсии.
19

Часть 3.
Классы функций, сохраняющих константу.
