1214

Пропускная способность непрерывных каналов связи

Непрерывным называется канал, который обеспечивает передачу непрерывных (аналоговых) сигналов.

Непрерывные сигналы, поступающие в канал связи из передатчика (Пд), описываются некоторой непрерывной функцией времени U(t).

Ограничения на значения этой функции задаются величиной средней мощности передаваемых сигналов P_v. Другой характеристикой непрерывного канала, как и канала дискретного, является полоса пропускания — интервал частот сигналов, которые могут распространяться в данном канале tt>mi_n — co_max. Если по своему физическому смыслу U является напряжением или силой электрического тока, то при неизменном электрическом сопротивлении канала связи Р_и ~ U², т.е. мощность сигнала определяет его амплитуду и средний квадрат значения параметра сигнала.

Сигнал на выходе канала V(t), поступающий в приемник (Пм), также является аналоговым. Он формируется в результате наложения помех, которые можно описать некоторой непрерывной функцией времени S(t), на входной сигнал; в результате: V(t) = U(t) ^п 5(f) (рис. 3.16). Под символом «и» понимается какая-либо композиция полезного сигнала и помехи. Чаще применяется аддитивная модель помех, когда информационный сигнал складывается с помехой, реже — мультипликативная модель, когда сигналы перемножаются.

Явный вид функции помех заранее неизвестен. Поэтому для количественного описания прохождения сигналов по непрерывному каналу приходится принимать ту или иную модель помех и модель канала. Наиболее распространенной является модель гауссовского канала: принимается, что помехи, будучи непрерывными случайными величинами, подчиняются нормальному (гауссовскому) статистическому распределению с математическим ожиданием (средним значением), равным нулю (т[8] = 0):

Пусть сигнал   на выходе канала представляет собой сумму полезного сигнала   и шума  , т.е.  , причем   и   статистически независимы. Допустим, что канал имеет ограниченную полосу пропускания шириной  . Тогда в соответствии с теоремой Котельникова (см. п. 1.5) функции  ,   и   можно представить совокупностями отсчетов  ,  , и  ,  , где  . При этом статистические свойства сигнала   можно описать многомерной ПРВ  , а свойства шума – ПРВ  .

Пропускная способность непрерывного канала определяется следующим образом:

,

где      – количество информации о какой-либо реализации сигнала   длительности T, которое в среднем содержит реализация сигнала   той же длительности  , а максимум ищется по всем возможным распределениям  .

Когда сигнал на входе канала имеет нормальное распределение и отсчеты независимы величина   максимизируется [6]. Поэтому пропускная способность гауссовского канала с дискретным временем, рассчитанная на единицу времени, с учетом (4.16) может быть записана в виде

.

(4.17)

Полученное выражение показывает, что пропускная способность гауссовского канала с дискретным временем определяется числом импульсов, передаваемых в секунду, и отношением сигнал/шум ( ).

С учетом взаимосвязи скорости передачи информации и полосы частот непрерывного канала от (4.17) можно перейти к формуле Шеннона, которая устанавливает связь пропускной способности гауссовского канала с полосой пропускания непрерывного канала и отношением мощности сигнала к мощности помехи:

.

(4.18)

График отношения   изображен на рис. 4.6. Заметим, что при малом отношении 

,

а пропускная способность канала связи прямо пропорциональна этому отношению.

При большом отношении   в (4.18) можно пренебречь единицей и считать, что

,

т.е. зависимость пропускной способности непрерывного канала от отношения сигнал/шум логарифмическая.

Пропускная способность канала, как предельное значение скорости безошибочной передачи информации, является одной из основных характеристик любого канала.

Определим пропускную способность стандартного канала тональной частоты, имеющего границы эффективно передаваемых частот   кГц, среднюю мощность сигнала на выходе 56 мкВт при средней мощности помехи 69000 пВт.

Согласно (4.18), при заданных параметрах

[бит/с].

Эпсилон-энтропия источника непрерывных сообщений

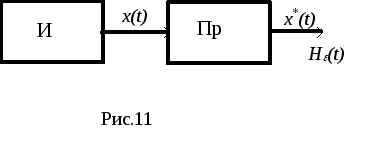
Сигнал на выходе источника(И) рис.11 непрерывных сообщений (например, микрофона, телефона, датчика температуры и пр. ) представляет собой непрерывный случайный процесс, энтропия которого в любом из сечений в общем случае равна бесконечности как это было показано в разделе 12. Такое количество информации не может быть передано по реальному каналу связи, пропускная способность которого всегда ограничена. Это и не нужно, так как скорость восприятия информации любым потребителем на выходе канала всегда ограничена его физическими возможностями. Поэтому непрерывный сигнал на выходе канала связи даже без помех отличается от сигнала на входе, так как содержит не всю информацию о нем (причем под каналом связи можно понимать любое преобразование одного ансамбля сигналов в другое: модуляцию, усиление, дискретизацию и пр.). Уже преобразование непрерывного сообщения в сигнал соответствующим устройством( микрофоном или др. датчиком сигнала) связано с потерей части информации, а сигнал отображает сообщение лишь с некоторой точностью

e(t)= x(t)- x*(t),

где x(t)-сигнал на входе преобразователя;

x*(t)- сигнал на выходе преобразователя(Пр) или оценка входного сигнала преобразователем, который всегда представляет собой некоторое решающее устройство, работающее по определенному правилу и заданному критерию качества.

Критерий качества, как известно, определяется потребителем информации, например, среднеквадратическое отклонение

e_ср=m{[ x(t)- x*(t)]²} , (42)

или дисперсия ошибки

.

Эпсилон-энтропией H_e(x)( e- энтропией) называется минимальное количество информации, которое должно содержаться в выходном сигнале x*(t) о входном сигнале x(t), чтобы этот сигнал можно было восстановить с заданной точностью e_ср.

H_e(x)=min I(x,x^*)=H(x)- max H(x/x^*), (43)

где

I(x,x^*)-взаимная информацияx и x^*;

H(x)и H(x/x^*)- соответственно, дифференциальная энтропия сигналаx(t) и условная энтропияx(t), когдаx*(t) известно;

min иmax берутся по всевозможным условным распределениямw(x/x^*).

В общем случае, когда сигнал (или сообщение) x(t)является гауссовским с дисперсией , ошибкаe(t) также является гауссовской с дисперсией , а с учетом аддитивного характера ошибкиe(t)условная энтропияH(x/x^*) полностью определяется дифференциальной энтропиейH(e).Соответственно,max H(x/x^*)= max H(e)= .

Тогда e- энтропия одного сечения гауссовского источника (e- энтропия одного отсчета)

H_e(x)=  - = 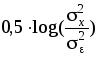.(44)

Величина  показывает отношение мощности(дисперсии) сигналаx(t)к мощности (дисперсии) ошибки, при котором среднеквадратическое отклонение сигналовx(t)иx^*(t) не превышаетs_e.

Следовательно, производительность источника непрерывных сообщений можно определить как количество информации, которое необходимо передавать в единицу времени, чтобы восстановить сообщение с заданной точностью.

H^’_e(x)=v× H_e(x),(45)

где v=1/Dt - скорость передачи отсчетов на выходе источника,Dt - интервал между отсчетами.

Для стационарного сигнала с ограниченным спектром Dt=1/(2F_max), тогдаH^’_e(x)= 2F_max × H_e(x).

Если, кроме того, источник является гауссовским, то

H^’_e(x)= F_max .(46)

Количество информации, выдаваемое гауссовским источником за время T_c , равноT_c× H^’_e(x)= T_c× F_max ,(47)

что совпадает с формулой для объёма сигнала, когда динамический диапазон сигнала D_c= .

Это значит, что объем сигнала на выходе источника равен количеству информации (46), которое содержится в сигнале для его воспроизведения с заданной точностью .

Для канала с пропускной способностью С, на входе которого подключен источник с производительностьюH^’_e(x), теорема К.Шеннона для канала с шумами принимает вид:

Если при заданном критерии точности источника (например,s_e) его эпсилон- производительность меньше пропускной способности канала H^’_e(x)< С, то существует способ кодирования (преобразования сигнала), при котором неточность воспроизведения сколь угодно близка к s_e; при H^’_e(x)> С такого способа не существует.

Теорема К.Шеннона определяет предельные возможности согласования источника непрерывных сообщений с каналом связи. Практически это достигается применением помехоустойчивых видов модуляции и кодирования.

Теорема Котельникова.

   Для того, чтобы восстановить исходный непрерывный сигнал из дискретизированного с малыми искажениями (погрешностями), необходимо рационально выбрать шаг дискретизации. Поэтому при преобразовании ана­логового сигнала в дискретный обязательно возникает вопрос о величине шага дискретизации  . Интуитивно нетрудно понять следующую идею. Ес­ли аналоговый сигнал обладает низкочастотным спектром, ограниченным некоторой верхней частотой F_e, (т.е. функция u(t) имеет вид плавно изме­няющейся кривой, без резких изменений амплитуды), то вряд ли на некото­ром небольшом временном интервале дискретизации   эта функция может существенно изменяться по амплитуде.    Совершенно очевидно, что точность восстановления аналогового сиг­нала по последовательности его отсчетов зависит от величины интервала дискретизации  . Чем он короче, тем меньше будет отличаться функция u(t) от плавной кривой, проходящей через точки отсчетов. Однако с уменьшени­ем интервала дискретизации   существенно возрастает сложность и объем обрабатывающей аппаратуры. При достаточно большом интервале дискре­тизации   возрастает вероятность искажения или потери информации при восстановлении аналогового сигнала.

   Оптимальная величина интервала дискретизации устанавливается тео­ремой Котельникова (другие названия — теорема отсчетов, теорема К. Шеннона, теорема X. Найквиста: впервые теорема была открыта в мате­матике О. Коши, а затем описана повторно Д. Карсоном и Р. Хартли), дока­занной им в 1933 г. Теорема В. А. Котельникова имеет важное теоретическое и практическое значение: дает возмож­ность правильно осуществить дискре­тизацию аналогового сигнала и опреде­ляет оптимальный способ его восста­новления на приемном конце по отсчетным значениям.

 Рис.14.1. Представление спектральной плотности

  Согласно одной из наиболее из­вестных и простых интерпретаций тео­ремы Котельникова, произвольный сиг­нал u(t), спектр которого ограничен некоторой частотой F_e может - быть полностью восстановлен по последо­вательности своих отсчетных значений, следующих с интервалом времени

                                            (1)

   Интервал дискретизации   и частоту F_e (1) в радиотехнике часто называют соответственно интервалом и частотой Найквиста. Аналитически теорема Котельникова представляется рядом

                         (2)

где k — номер отсчета;   — значение сигнала в точках отсчета;   — верхняя частота спектра сигнала.

   Для доказательства теоремы Котельникова рассмотрим произвольный непрерывный сигнал и(t), спектральная плотность   которого сосредото­чена в полосе частот   (сплошная линия на рис.14.1).

   Мысленно дополним график спектральной плотности   симметрично значениям, повторяющимся с периодом  , (штриховые линии на рис.14.1). Полученную таким образом периодическую функцию разложим в ряд Фу­рье, заменив в формуле

аргумент t на с  , частоту   на   и (фор­мально) п на k. Тогда

                                   (3)

Полагая, что в соотношении

период — это  , а интервал дис­кретизации   запишем

                             (4)

   Воспользуемся формулой обратного преобразования Фурье  и представим исходный непрерывный сигнал в следующем виде:

                 (5)

   Таким же образом запишем значение дискретизированного сигнала для некоторого k-то отсчета времени. Поскольку время  , то

   Сравнив это выражение с формулой для C_k , замечаем, что   С учетом этого соотношения спектральная функция (3), после несложных преобра­зований, примет вид:

             (7)

   Затем проделаем следующее: подставим выражение  в соотношение  , изменим порядок интегрирования и суммирования, представим отно­шение как  , и вычислим интеграл.

   В результате получим такую фор­мулу:

   Из этого соотношения следует, что непрерывная функция u(t) дейст­вительно определяется совокупностью ее дискретных значений амплиту­ды в отсчетные моменты времени  , что и доказывает теорему Ко­тельникова.

   Простейшие сигналы вида   ортогональные друг другу на интерва­ле времени - ,  , называются функ­циями отсчетов, базисными функция­ми, или функциями Котельникова. График k-й функции Котельникова представлен на рис. 2. Каждая из ба­зисных функций s_k(t) сдвинута относи­тельно подобной ближайшей функции s_k-1(t) или s_k+1(t) на интервал дискрети­зации  . Элементарный анализ фор­мулы (10) и графика на рис. 14.3 пока­зывает, что сигнал s_k(t) отражается

 Рис. 14.2. График базисной функции Котельникова

Рис.14.3. Аппроксимация непрерывного сигнала рядом Котельникова функцией sinx/x, которая также характеризует огибающую спектральной плотности прямоугольного импульса.

  Представление (точнее, аппроксимация) заданного непрерывного сигнала u(t) рядом Котельникова (2) иллюстрируется диаграммами на рис. 14.3. графике (здесь базисные функции  для упрощения показаны без аргумента t построены четыре первых члена ряда, соответствующие отсчетам сигнала в моменты времени 0,  , 2  и 3 , взятым в соответствии с теоремой Котельникова. При суммировании этих членов ряда в любые отсчетные моменты времени kDt, непрерывный сигнал абсолютно точно аппроксимируется независимо от числа выбранных отсчетов. В интервале же между любыми отсчетами сигнал u(t) аппроксимируется тем точнее, чем больше суммируется членов ряда Котельникова (2).

Оценим возможность применения теоремы Котельникова к импульсному сигналу u(t) конечной длительности T_х. Как известно, такие сигналы теоретически обладают бесконечно широким спектром. Однако на практике  можно ограничиться некоторой верхней частотой F_в за пределами которой в спектре содержится пренебрежительно малая доля энергии по сравнению с энергией всего исходного сигнала. В радиотехнике таким критерием является содержание 90% средней мощности сигнала в границах спектра. В этом случае сигнал u(t) длительностью T_х с верхней граничной частотой спектра F_в может быть представлен рядом Котельникова с определенным, ограниченным числом отсчетов

                    (10)

   Здесь  — число отсчетов.

 Рис.14.4. Представление прямоугольного импульса отсчетами:

о—двумя; б—тремя