новая папка 1 / 773161

УДК 517.9(07)

ББК 22.161.6я7

Р49

Печатаются по решению методической комиссии факультета управления и автоматизации

Рецензенты: проф. Ю. В. Малышев проф. Н. К. Нуриев

Составитель доц. В. Р. Ризаев

Дифференциальные уравнения первого порядка Клеро и Лагранжа

Р49 и методы их решения : методические указания / сост. В. Р. Ризаев; Минобрнауки России, Казан. нац. исслед. технол. ун-т.

– Казань : Изд-во КНИТУ, 2017. – 28 с.

Рассмотрены методы решения дифференциальных уравнений первого порядка, не разрешенных относительно производных типа Клеро и Лагранжа, которые используются при выполнении расчетов аппаратов химических производств.

Предназначены для бакалавров технологической направленности, изучающих дисциплины «Математика», «Высшая математика».

Подготовлены на кафедре высшей математики.

УДК 517.9(07)

ББК 22.161.6я7

2

Цель работы: освоение методов решения дифференциальных уравнений І порядка, не разрешенных относительно производных и дифференциальных уравнений в полных дифференциалах, которые используются при выполнении расчетов аппаратов химических производств.

В1969 году И. Бернулли поставил и решил следующую задачу о кривой скорейшего спуска, имеющую естественно-научную значимость.

Ввертикальной плоскости даны две точки А и В, не лежащие на одной вертикали. Требуется найти такую кривую, соединяющую эти две точки, по которой под действием силы тяжести скатывается материальная точка за кратчайшее время и при спуске проходит через среду с возрастающей плотностью.

Эта задача связана с аналогичной задачей в оптике о траектории луча света, когда последний проходит через среду переменной плотности. При этом луч света при переходе от слоя к слою преломляется все более и более, а его скорость падает, но при этом величина

(а)

остается постоянной (α — угол между лучом и нормалью к слою среды). Для того чтобы задачу записать через дифференциальное уравнение,

представим, что материальная точка (подобно лучу света) способна выбрать себе такую траекторию спуска, чтобы время спуска было наименьшим. Тогда справедлива приведенная формула (а). Введем систему координат, как показано на рисунке.

Исходя из закона сохранения энергии потенциальная энергия материальной точки в точке А ( ) равна ее кинетической энергии в

точке траектории с ординатой y.

3

Copyright ООО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

где g — ускорение свободного падения. С другой стороны, из рисунка

Уравнение (г) и определяет вид траектории материальной точки. Решив его, можно показать, что такой кривой линией является циклоида.

Изучив методические указания, найдите решение уравнения (г).

4

1. ОСНОВНЫЕ ПОНЯТИЯ

Общий вид дифференциального уравнения І порядка:

), придав конкретное численное значение константе С.

Определение. Решение (интеграл) дифференциального уравнения, которое не получается из общего решения (общего интеграла) ни при каком значении С, называется особым.

Геометрический смысл особого решения — огибающая однопара-

от параметра С, называется линия, которая в каждой своей точке касается какой-нибудь из линий семейства. В различных своих точках она касается разных линий семейства.

Пусть

и в этой точке удовлетворяют уравнению. Но для огибающей значения и в той же точке 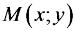будут теми же.

Рис. 1.1

5

Следовательно, огибающая также является интегральной кривой, и притом особой, поскольку через каждую точку огибающей по одному направлению проходят две интегральные кривые: сама огибающая и ка- кая-либо из кривых семейства.

Чтобы получить особое решение (особый интеграл) уравнения (1.1), надо исключить С из системы уравнений:

где φ(x; y;c)= 0 — общий интеграл уравнения (1.1). Особый интеграл будет иметь вид ϕ(x; y)= 0.

Замечание. Надо иметь в виду, что эта система уравнений может вообще не определять никакой кривой; тогда уравнение не будет иметь особого интеграла.

2. УРАВНЕНИЕ КЛЕРО

Определение. Уравнением Клеро называется дифференциальное

Уравнение решается методом введения параметра. Он заключается в том, что рассматриваемые переменные выражаются через параметр и ре-

Для выражения x через p продифференцируем по x:

y′ = p + x dpdx +ϕ′( p) dpdx ,

6

или

p = p + x dpdx +ϕ′( p) dpdx .

Отсюда

dpdx (x +ϕ′( p))= 0.

Возможны два случая:

1. dpdx = 0, p = c.

Подставив с вместо p:

y = xc +ϕ(c),

получим общее уравнение Клеро.

Геометрически его решение представляет собой семейство кривых. 2. Приравниваем нулю второй сомножитель:

x +ϕ′( p) = 0.

Это уравнение совместно с (2.2) тоже дает решение уравнения Клеро в параметрической форме:

Исключая из двух уравнений (2.3) параметр p, получим интеграл уравнения Φ(x; y)= 0. Этот интеграл не содержит С и, следовательно, не

может быть общим интегралом.

Он не может быть также получен из общего ни при каких значениях С, так как не является линейной функцией. Это так называемый особый интеграл.

Пример 1. Найти общее и особое решение уравнения

7

y = xy′+ y1′.

1) Положим y′ =C. Получим общее уравнение

y = Cx + C1 .

Это множество прямых.

2) Для получения особого решения положим y′ = p :

y = px + 1p .

Продифференцируем по x:

Получим решение в параметрической форме:

x = 1 ;p2

y = 2 .p

Это особое решение.

8

Исключаем параметр p. Для этого возведем обе части второго уравнения в квадрат и разделим их на соответствующие части первого урав-

Геометрически особый интеграл представляет параболу (рис. 2.1).

Рис. 2.1

Из чертежа видно, что особый интеграл (парабола) оказался огибающей семейства интегральных прямых, определяемых общим решением.

Пример 2. Решить уравнение

Решение

1) Общий интеграл получаем, заменяя y′ на с:

y = xc + 1ac+c2 .

2) Особое решение. Положим y′ = p.

9

y = xp + 1ap+ p2 .

Продифференцируем по x:

Особое решение в параметрической форме:

в степени 2/3 и, складывая почленно, получаем астроиду:

10