
новая папка 1 / 231950
.pdfМинистерство сельского хозяйства Российской федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Саратовский государственный аграрный университет имени Н.И. Вавилова»
МЕТОДЫ РЕШЕНИЯ МАТРИЧНЫХ ИГР
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ЗАДАНИЯ ДЛЯ РАССЧЁТНО-ГРАФИЧЕСКОЙ РАБОТЫ
для студентов-бакалавров аграрного университета направлений подготовки землеустройство и кадастры, экономика и менеджмент
Саратов 2014

УДК 51-7(519.2/.6) ББК 22.18
У 32
У32 Методы решения матричных игр: методические указания и задания для рассчётно-графической работы для студентов-бакалавров аграрного университета направлений подготовки землеустройство и кадастры, экономика и менеждмент / Сост. Н.Б. Уейская //ФГБОУ ВПО «Саратовский ГАУ». - Саратов, 2014 – с. 15.
Данные указания для выполнения рассчётно-графической работы по теме «Методы решения матричных игр» составлены в соответствии с программами дисциплин: «Математические методы принятия решений» для студентов-бакалавров направления Землеустройство и кадастры, «Методы оптимальных решений» для направления Экономика и «Теория игр в менеджменте» направления Менеджмент. Приведены необходимые сведения, образец выполнения работы и варианты заданий.
УДК 51-7(519.2/.6) ББК 22.18
© Уейская Н.Б., 2014 © ФГБОУ ВПО «Саратовский ГАУ», 2014
2
Введение.
В условиях рыночной экономики полагаться только на качественный анализ явлений и интуицию становится очень ненадёжно, поэтому возрастает роль математических методов, используемых в задачах принятия управленческих решений. Механизмы функционирования рынка, конкуренции, возникновения или распада монополий, а также способы принятия решений в условиях конкурентной борьбы, игры монополий, действующие в экономической реальности, не могут быть исследованы и поняты без теории игр.
Данные указания для выполнения рассчётно-графической работы по теме «Методы решения матричных игр» составлены в соответствии с программами дисциплин: «Математические методы принятия решений» для студентов-бакалавров направления Землеустройство и кадастры, «Методы оптимальных решений» для направления Экономика и «Теория игр в менеджменте» направления Менеджмент. Приведены необходимые сведения, образец выполнения работы и варианты заданий.
Содержит следующие разделы: решение матричных игр в чистых стратегиях, а также графоаналитическим методом, методами линейного программирования и методом Брауна в смешанных стратегиях. Кроме того, проводится оценка стратегий игрока для игр с природой по различным критериям.
Данные указания ориентированы на формирование у студентов ключевых компетенций, связанных с пониманием основных понятий по указанным разделам, на применение теоретико-игровых методов в профессиональной деятельности.

ПРИМЕР ВЫПОЛНЕНИЯ РАБОТЫ
Задание 1. Фирма может выставить на рынок три вида товара. В зависимости от состояния рынка её доходы в денежных единицах представлены в таблице:
Виды |
Состояния рынка |
|
|
|
товаров |
1 |
2 |
3 |
4 |
1 |
1 |
0 |
-2 |
2 |
2 |
2 |
1 |
3 |
1 |
3 |
-3 |
-2 |
4 |
-2 |
Требуется составить модель матричной игры и найти а) нижнюю цену игры и все максиминные стратегии игрока 1;
б) верхнюю цену игры и все минимаксные стратегии игрок 2; в) цену игры и седловые точки, если они существуют;
г) рассматривая её как игру с природой, найти оптимальные стратегии игрока 1 по
критериям Вальда, Гурвица (полагая коэффициент пессимизма |
= 0,2 и =0,5), |
Сэвиджа и Лапласа. |
|
Решение. Составим модель матричной игры. |
|
Множество игроков I={1, 2}, где 1 – фирма, 2 – рынок. Множество стратегий |
|
(возможных действий) игрока 1 обозначим S1 {1,2,3} , элементы которого есть виды |
|
товаров. Для игрока 2 его множество стратегий S2 {1,2,3,4} , |
элементы которого |
представляют собой состояния рынка, а матрица игры, элементы которой равны доходам в денежных единицах игрока 1 в во всевозможных ситуациях (определяются
|
1 |
0 |
2 |
2 |
|
парой стратегий выбранных игроками), равна |
А= 2 |
1 |
3 |
1 |
. Если |
|
3 |
2 |
4 |
2 |
|
предположить, что среда ведёт себя наихудшим образом по отношению к принимающему решение, то игру можно рассматривать как матричную.
а). Для нахождения нижней цены игры и максиминных стратегий игрока 1 в каждой строке платёжной матрицы выбираем минимальный элемент (наименьший возможный выигрыш игрока 1 при применении соответствующей стратегии) и выписываем его в отдельный столбец. Затем выбираем в построенном столбце максимальный элемент или элементы, если их окажется несколько, и отметим их звёздочкой. Он (они) и будут равны нижней цене игры, а номера строк, в которых расположены эти элементы будут соответствовать максиминным стратегиям игрока 1. В нашем случае имеем:
|
|
|
|
minaij |
|
|
|
|
j |
1 |
0 |
2 |
2 |
2 |
2 |
1 |
3 |
1 |
1* |
3 |
2 |
4 |
2 |
3 |
Таким образом, нижняя цена игры v = m a xm i naij =1, а максиминная стратегия игрока |
|
i |
j |
1 (соответствует номеру строки, отмеченной звёздочкой): i* 2 .
4

б). Для нахождения верхней цены игры и минимаксных стратегий игрока 2 находим в каждом столбце платёжной матрицы максимальный элемент (наибольший возможный проигрыш игрока 2 при применении соответствующей стратегии) и выписываем его в отдельную строку, а затем выбираем в построенной строке минимальный элемент или элементы, если их окажется несколько, и также отметим их звёздочкой. Он (они) и будут равны верхней цене игры, а номера столбцов, в которых расположены эти элементы будут соответствовать минимаксным стратегиям игрока 2.
|
1 |
0 |
2 |
2 |
|
|
|
|
2 |
1 |
3 |
1 |
|
|
|
|
3 |
2 |
4 |
2 |
|
|
|
maxaij |
2 |
1* |
4 |
2 |
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|||||
Таким образом, верхняя цена игры v = m i nm ax aij =1. Минимаксная стратегия |
|||||||
|
|
|
|
|
|
j |
i |
игрока 2: j* |
2 . |
|
|
|
|
|
|
в). Седловая точкаэто ситуация, выигрыш первого игрока в которой есть элемент, являющийся одновременно самым маленьким в своей строке и самым большим в своём
столбце. Такая ситуация существует, если v = v = v и образуется любой парой соответственно максиминной и минимаксной стратегий, при этом v называют ценой игры, а седловую точку её решением, так как ни одному из игроков невыгодно отклониться от неё в одностороннем порядке.
В нашем случае v=1. Седловая точка (2, 2).
г). Поскольку игрок 2 – рынок (стихийная сила), то игру можно рассматривать как игру с природой.
Оценим стратегии игрока 1, используя Критерий Вальда, основаный на гипотезе крайнего пессимизма игрока по отношению к поведению среды, а именно: предполагается, что среда ведёт себя наихудшим образом по отношению к принимающему решение.
Оптимальной стратегией по данному критерию является максиминная стратегия. В нашем случае это стратегия 2.
|
|
|
|
|
|
|
|
|
Таблица 1 |
|
Виды |
Состояния рынка |
Кр. |
maxaij |
Критерий Гурвица |
|
Кр. |
||||
товаров |
|
|
|
|
Вальда |
j |
|
|
|
Лапласа |
|
1 |
2 |
3 |
4 |
|
α =0,2 |
α =0,5 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
minaij |
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
-2 |
2 |
-2 |
2 |
1,2 |
0 |
|
0,25 |
2 |
2 |
1 |
3 |
1 |
1* |
3 |
2,6* |
2* |
|
1,75* |
3 |
-3 |
-2 |
4 |
-2 |
-3 |
4 |
2,6* |
0,5 |
|
-0,75 |
Критерий Гурвица. Гипотеза о поведении среды: наихудшее состояние наступает с вероятностью α, а наилучшее с вероятностью (1-α). α называют также коэффициентом пессимизма. Оптимальной по этому критерию считается та стратегия, для которой
среднеожидаемый выигрыш m i naij (1 |
)m a xaij является наибольшим. |
j |
j |
Оценим стратегии игрока при α=0,2 и 1- α=0,8:
5

Для стратегии 1: |
0,2 |
( |
2) |
0,8 |
2 |
1,2 |
Для стратегии 2: |
0,2 1 |
|
0,8 3 |
|
2,6 |
|
Для стратегии 3: |
0,2 |
( |
3) |
0,8 |
4 |
2,6 . |
Оптимальные стратегии: 2 и 3.
Аналогично, оценим стратегии игрока при α=0,5и 1- α=0,5:
Для стратегии 1: |
0,5 |
( |
2) |
0,5 |
2 |
0 . |
Для стратегии 2: |
0,5 1 |
|
0,5 3 |
|
2 . |
|
Для стратегии 3: |
0,5 |
( |
3) |
0,5 |
4 |
0,5 . |
Оптимальная стратегия: 2.
Критерий Лапласа. Гипотеза о поведении среды: предполагается, что все состояния среды равновероятны. Оптимальной по этому критерию является та стратегия, для которой среднее арифметическое возможных выигрышей будет наибольшим.
Для стратегии 1: |
(1 |
0 |
2 |
2) : 4 |
0,25 . |
Для стратегии 2: |
(2 |
1 |
3 |
1) : 4 |
1,75 . |
Для стратегии 3: |
( 3 |
2 |
4 |
2) : 4 |
0,75 . |
Оптимальная стратегия: 2. |
|
|
Результаты вычислений занесём в табл. 1. |
|
|
Критерий Сэвиджа основан на преобразовании матрицы |
выигрышей (aij ) в |
|
матрицу рисков (rij ) , где rij |
m a xaij aij . Риски показывают, |
какие потери понёс |
|
i |
|
игрок из-за незнания истинного состояния среды. Заметим, что матрица рисков всегда неотрицательна.
Оптимальной по данному критерию считается стратегия, минимизирующая максимальный риск.
Составим матрицу рисков и найдем минимаксную стратегию игрока 1. Результаты вычислений занесём в табл. 2. Оптимальная стратегия: 2.
|
|
|
|
|
|
|
|
Таблица 2 |
|
|
Виды |
Состояния рынка |
|
|
|
|
Критерий |
|
|
|
товаров |
|
|
|
|
|
|
Сэвиджа |
|
|
|
1 |
2 |
3 |
|
|
4 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
maxrij |
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
6 |
|
|
0 |
6 |
|
|
2 |
0 |
0 |
1 |
|
|
1 |
1* |
|
|
3 |
5 |
3 |
0 |
|
|
4 |
5 |
|
|
|
|
|||||||
Ответ: а) v =1; максиминная стратегия: 2; б) |
v =1; минимаксная стратегия: 2; в) |
||||||||
цена игры 1; седловая точка (2,2); г) оптимальная по критерию Вальда стратегия 2, выигрыш 1; оптимальные стратегии по критерию Гурвица ( = 0,2) 2 и 3, выигрыш 2,6; ( =0,5) стратегия 2 выигрыш 2; оптимальная по критерию Лапласа стратегия 2, выигрыш 1,75; оптимальная по критерию Сэвиджа стратегия 2, наибольший риск 1.
6
Задание 2. Требуется найти решение матричной игры а) графоаналитическим методом; б) методами линейного программирования; в) методом Брауна (10 итераций)
для игры, заданной матрицей |
2 |
3 |
11 . |
|
7 |
5 |
2 |
Решение. |
|
а) Найдём решение игры графоаналитическим методом. |
|
Построим на промежутке [0;1] отрезки прямых: |
|
v=2p+7(1-p) |
(I) |
v=3p+5(1-p) |
(II) |
v=11p+2(1-p), |
(III) |
задающих выигрыш v игрока 1, при условии, что игрок 2 примет чистую стратегию
соответственно 1, 2 и 3. |
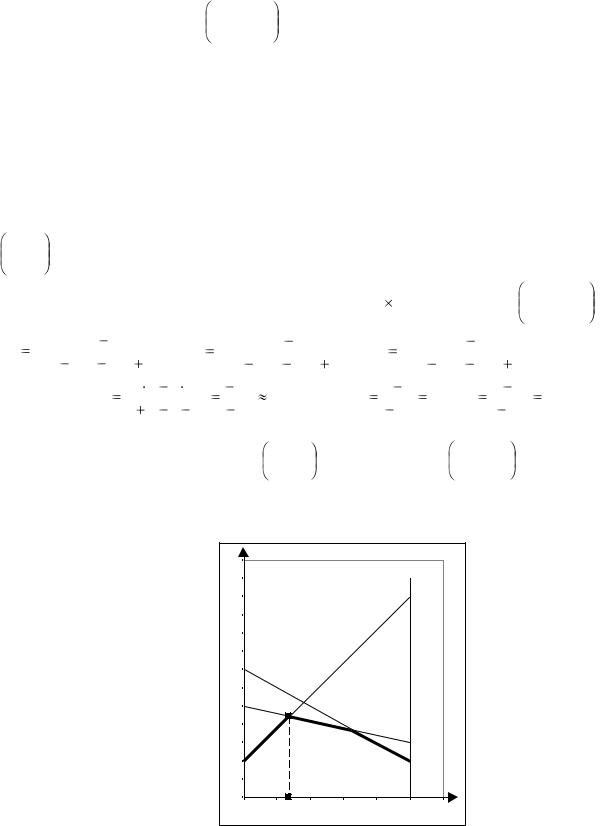
Затем построим нижнюю огибающую и найдём её наивысшую |
||||||||||||||||||||||||||||||||||||||||
точку М (см. рис. 1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Так как точка М есть точка пересечения прямых (II) и (III), то, исходя из матрицы |
||||||||||||||||||||||||||||||||||||||||
3 |
11 , |
найдём решение |
по |
формулам |
|
для нахождения |
|
оптимального |
решения |
||||||||||||||||||||||||||||||||
5 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a11 |
|
a12 |
|||
Х*=(р*, 1-р*) и |
|
|
У*=(q*, 1-q*) матричной игры |
2 |
2 с матрицей А= a21 |
|
a22 : |
||||||||||||||||||||||||||||||||||
p* |
|
a22 |
a21 |
|
|
; |
q* |
|
|
a22 |
a12 |
|
; |
v |
|
|
a11a22 |
|
a12a21 |
. |
|
|
|||||||||||||||||||
a11 |
a12 |
a21 |
a22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
a11 |
a12 |
a21 |
a22 |
|
|
|
a11 |
|
a12 |
|
a21 |
|
a22 |
|
|
|
|
||||||||||||||||||
|
Цена игры: v |
3 2 |
5 11 |
|
49 |
|
4,45 . |
|
p* |
2 |
5 |
|
3 |
|
; q* |
2 |
11 |
|
|
9 |
. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
3 |
2 |
5 |
11 |
11 |
|
|
|
|
|
|
|
|
|
|
11 |
|
11 |
|
|
|
|
|
|
11 |
|
11 |
|||||||||||
Оптимальная стратегия игрока 1: Х*= |
|
3 |
, |
8 |
|
, а игрока 2 - У*= |
0, |
|
9 |
, |
2 |
|
, так как его |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 11 |
|
|
|
|
|
|
|
|
|
|
|
11 11 |
|
|
|
|
|
||||||||||
чистая стратегия 1 не входила в решение.
|
|
|
|
Рис..1. |
|
|
13 |
|
|
|
|
|
|
12 |
|
|
|
|
|
|
11 |
|
|
|
|
|
11 |
10 |
|
|
|
|
|
|
9 |
|
|
|
|
|
|
8 |
|
|
|
|
|
|
7 |
7 |
|
|
|
|
|
6 |
|
|
|
|
|
|
5 |
5 |
|
|
|
|
|
4 |
|
|
|
|
|
|
3 |
|
|
|
|
|
3 |
2 |
2 |
|
|
|
|
2 |
1 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
0,2 |
0,4 |
0,6 |
0,8 |
1 |
1,2 |
7

б). Найдём решение методами линейного программирования.
Так как все элементы матрицы игры положительны, то цена игры v>0. Приходим к паре взаимно двойственных задач:
L=u1+u2+u3 (max) |
|
|
L1=t1+t2 (min) |
|
|
||||
2u1 |
3u2 |
11u3 |
1 |
|
2t1 |
7t2 |
1 |
|
|
|
3t1 |
5t2 |
1 |
|
|||||
7u1 |
5u2 |
2u3 |
1 |
и |
. |
||||
11t1 |
2t2 |
1 |
|||||||
u1 |
0,u2 |
0, u3 |
0 |
|
|
||||
|
t1 |
0, t2 |
0 |
|
|||||
|
|
|
|
|
|
||||
Решим эти задачи симплекс–методом. Для чего приведём первую задачу к канонической форме:
2u1 |
3u2 |
11u3 |
u4 |
1 |
|
|
|
|
|
7u1 |
5u2 |
2u3 |
u5 |
1 , где u4 ≥0 и u5 ≥ 0. |
|
|
|
||
L |
u1 |
u2 u3 |
0 |
|
|
|
|
|
|
Составим симплексную таблицу: |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
БП |
|
|
СЧ |
|
u1 |
u2 |
u3 |
u4 |
u5 |
u4 |
|
|
1 |
|
2 |
3 |
11 |
1 |
0 |
u5 |
|
|
1 |
|
7 |
5 |
2 |
0 |
1 |
L |
|
|
0 |
|
-1 |
-1 |
-1 |
0 |
0 |
Выберем разрешающий столбец, который соответствует наименьшему отрицательному коэффициенту в строке L. Возьмём, например, u2. Выбираем вторую строку разрешающей, так как для неё отношение свободного члена к положительному элементу разрешающего столбца минимально.
Составим вторую таблицу, в которой первая строка получена делением разрешающей строки на разрешающий элемент 5; вторая есть результат сложения первой строки второй таблицы, умноженной на(-3) с первой строкой первой таблицы. Строка L есть сумма соответствующей строки первой таблицы с первой строкой второй таблицы.
БП |
СЧ |
u1 |
u2 |
u3 |
u4 |
u5 |
u2 |
0,2 |
1,4 |
1 |
0,4 |
0 |
0,2 |
u4 |
0,4 |
-2,2 |
0 |
9,8 |
1 |
-0,6 |
L |
0,2 |
0,4 |
0 |
-0,6 |
0 |
0,2 |
Во второй таблице разрешающий столбец u3, а разрешающая строка вторая. Поделим её на разрешающий элемент 9,8 и запишем в первой строке третьей таблицы, а затем преобразуем её так, чтобы в столбце u3 остальные элементы обратились в нуль. Для этого первую строку третьей таблицы умножим на (-0,4) и сложим с первой строкой второй таблицы. Строка L третьей таблицы получается сложением соответствующей строки второй таблицы с первой строкой этой же таблицы, умноженной на 0,6. В результате получаем таблицу
БП |
СЧ |
u1 |
u2 |
u3 |
u4 |
u5 |
u3 |
2/49 |
- 11/49 |
0 |
1 |
5/49 |
-3/49 |
u2 |
9/49 |
73/49 |
1 |
0 |
-2/49 |
11/49 |
L |
11/49 |
13/49 |
0 |
0 |
3/49 |
8/49 |
8

Так как все коэффициенты в строке L неотрицательны, то преобразования закончены. Из последней таблицы можно найти решение двойственных задач, а именно: в двойственных задачах свободные члены в неравенствах и коэффициенты в целевой функции меняются местами, и поэтому решение двойственной задачи
находится в строке L последней таблицы в столбцах u4 и u5. Таким образом, Lmax= 4911 ,
t*= |
|
3 |
, |
8 |
, |
|
u*= 0, |
9 |
, |
2 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
49 49 |
|
|
|
|
|
|
|
49 49 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Следовательно, цена игры v = |
49 |
≈4,45. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
р*1= |
|
3 49 |
|
3 |
; р*2= |
8 |
|
49 |
|
8 |
и Х*= |
|
3 |
, |
8 |
. |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
49 |
|
11 |
|
11 |
|
|
11 |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
49 |
|
|
11 |
|
11 11 |
|
|
|||||||||||||||||||||||
|
|
q*1=0; |
q*2= |
9 |
|
49 |
|
|
|
9 |
; q*3= |
|
2 |
|
49 |
и У*= 0, |
9 |
, |
2 |
. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
49 |
11 |
|
11 |
|
|
|
|
|
|
|
49 |
11 |
|
|
|
|
11 11 |
|||||||||||||
в). Найдём методом Брауна приближённое решение игры после 10 итераций. Игроки по очереди выбирают свои стратегии. Первый начинает с максиминной. Его
возможные выигрыши (проигрыши игрока 2) записываем в отдельную строку, расположенную ниже матрицы. Второй игрок выбирает стратегию, обеспечивающую ему наименьший проигрыш. Теперь возможные выигрыши первого игрока записываем в отдельный столбец справа от матрицы. Он выбирает стратегию, обеспечивающую ему наибольший выигрыш. Каждый раз выбранные стратегии отмечаем звёздочкой. Затем подсчитываем сумму возможных проигрышей игрока 2 за две партии и записываем в следующую строку ниже предыдущей. Для игрока 2 снова отмечаем звёздочкой стратегию, гарантирующую ему наименьший суммарный проигрыш за две партии. Записываем суммарные выигрыши первого игрока за две партии, и отмечаем звездочкой стратегию, обеспечивающую ему наибольший суммарный выигрыш за две партии и т.д.
Вычисления поместим в таблицу, крайний левый столбик которой служит для определения максиминной стратегии игрока 1.
2* |
2 |
3 |
11 |
2 |
5 |
8 |
19* |
22 |
25 |
28 |
39* |
42* |
45 |
2 |
7 |
5 |
2 |
7* |
12* |
17* |
19 |
24* |
29* |
34* |
36 |
41 |
46* |
|
2* |
3 |
11 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
9 |
8* |
13 |
2 |
|
|
|
|
|
|
|
|
|
|
16 |
13* |
15 |
3 |
|
|
|
|
|
|
|
|
|
|
23 |
18 |
17* |
4 |
|
|
|
|
|
|
|
|
|
|
25 |
21* |
28 |
5 |
|
|
|
|
|
|
|
|
|
|
32 |
26* |
30 |
6 |
|
|
|
|
|
|
|
|
|
|
39 |
31* |
32 |
7 |
|
|
|
|
|
|
|
|
|
|
46 |
36 |
34* |
8 |
|
|
|
|
|
|
|
|
|
|
48 |
39* |
45 |
9 |
|
|
|
|
|
|
|
|
|
|
50 |
42* |
56 |
10 |
|
|
|
|
|
|
|
|
|
По количеству звёздочек в достроенных строках и столбцах соответственно
находим: |
|
Х10 = (0,3; 0,7); |
У10= (0,1; 0,7; 0,2). |
9 |
|

|
|
|
|
|
|
2 |
3 |
11 |
|
0,1 |
|
|
|
2 |
3 |
|
11 |
|
1 |
|
|
|
|
|
v10=X10AУ10Т=(0,3;0,7) |
|
0,7 |
=0,1·0,1 (3;7) |
|
|
7 |
= |
|
|
|||||||||||||
|
7 |
5 |
2 |
|
7 |
5 |
|
2 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
0,2 |
|
|
|
|
|
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
=0,01 (3;7) 2 1 |
3 7 |
|
11 2 |
=0,01(3;7) |
45 |
=0,01(3·45+7·46)= 4,57. |
|
|
|
|||||||||||||
|
|
7 1 |
5 |
7 |
|
2 |
2 |
|
|
|
|
46 |
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: а) и б) v |
4,45 : Х*= |
3 , |
8 |
, |
У*= |
0, 9 |
, 2 |
. в) v10= 4,57 ; Х10 |
= (0,3; 0,7); |
|||||||||||||
|
|
|
|
|
|
|
|
|
11 11 |
|
11 11 |
|
|
|
|
|
|
|
|
|
|||
У10= (0,1; 0,7; 0,2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Пример выполнения задания 2а), когда игра имеет формат m |
2 . |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть игра задана матрицей |
3 |
5 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
11 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Построим на промежутке [0;1] отрезки прямых: |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
v=2q+7(1-q) |
|
|
|
|
|
|
|
|
|
|
|
(I`) |
|
|
|||||
|
|
|
|
v=3q+5(1-q) |
|
|
|
|
|
|
|
|
|
|
|
(II`) |
|
|
|||||
|
|
|
|
v=11q+2(1-q), |
|
|
|
|
|
|
|
|
|
|
|
(III`) |
|
|
|||||
задающих выигрыш v игрока 1, при условии, что он примет чистую стратегию |
|||||||||||||||||||||||
соответственно 1, 2 и 3, а второй игрок примет стратегию У= (q,1 |
q) . Затем построим |
||||||||||||||||||||||
верхнюю огибающую и найдём её низшую точку N (см. рис.2). Так как точка N есть |
|||||||||||||||||||||||
точка пересечения прямых (I`) и (III`), то, исходя из матрицы |
|
2 |
7 |
, найдём решение |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
2 |
|
|
|
|
|
по тем же формулам, |
что и для игр формата 2 |
n : |
v |
2 |
2 |
7 11 |
73 |
5,21; |
|||||||||||||||
2 |
|
2 |
7 |
|
11 |
14 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
p* |
2 11 9 ; q* |
|
2 7 5 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
14 |
14 |
|
|
14 |
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0,2 |
|
0,4 |
0,6 |
0,8 |
1 |
1,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.2. |
|
|
|
|
|
|
|
|
|
|
|
||
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
