новая папка 1 / 231808
.pdfМинистерство сельского хозяйства Российской Федерации.
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Саратовский государственный аграрный университет имени Н.И. Вавилова»
Методические указания и задания для выполнения самостоятельной работы
по курсу «МАТЕМАТИКА»
Ч1. линейная алгебра
Направление подготовки
080200.62. Менеджмент
Профиль подготовки
Производственный менеджмент (агропромышленного комплекса) Маркетинг
Производственный менеджмент (природопользования) Управленческий и финансовый учёт
Производственный менеджмент предприятий (пищевой промышленности)
Саратов 2013
Математика: методические указания и задания для выполнения самостоятельной работы по направлению подготовки 080200.62 Менеджмент/ Сост.:Г. Н. Камышова, Н. Н. Терехова// ФГБОУ ВПО «Саратовский ГАУ». – Саратов, 2013. –19 С.
Методические указания для выполнения самостоятельной работы по направлению подготовки 080200.62 Менеджмент содержат теоретический материал, примеры и задания к выполнению самостоятельной работы по курсу «Математика». Направлены на формирование у студентов навыков расчёта математических задач. Материал ориентирован на вопросы общекультурной и профессиональной компетенций будущих специалистов.
© ФГБОУ ВПО «Саратовский ГАУ», 2013
3
ВЕДЕНИЕ
Вметодическом указании для выполнения самостоятельной работы по направлению подготовки 080200.62 Менеджмент изложен необходимый материал по курсу “Математика”, применяемый при решении конкретных задач: линейной алгебры. Авторы приводят основные понятия по курсу “Математика”, приёмы расчётов. Материал раздела проиллюстрирован примерами и сопровождается подборкой задач для самостоятельной работы.
Вметодическом указании для выполнения самостоятельной работы по направлению подготовки 080200.62 Менеджмент использованы материалы, прошедшие практическую проверку при преподавании курса “Математика”.
При изложении материала применяются традиционные обозначения и термины. Данное методическое указание, позволит будущим специалистам менеджерам
приобрести необходимые базовые навыки, расширить кругозор, повысить уровень мышления и общую культуру. Всё это понадобится для ориентации в профессиональной деятельности и успешной работе.
4
1. ЛИНЕЙНАЯ АЛГЕБРА Цель: изучение понятия матрицы, действия над матрицами, решение систем
линейных уравнений различными методами. |
|
|||
1.1 . Действия с матрицами |
|
|||
Теоретический материал |
|
|||
Определение: Матрицей размера |
m n называется совокупность |
m n чисел, |
||
расположенных в виде прямоугольной таблицы из m строк и n столбцов. |
|
|||
Определение: Матрица размера 1 |
n называется матрицей – строкой. |
|
||
Определение: Матрица размера m 1 называется матрицей – столбцом. |
|
|||
Определение: Матрица размеров n |
n называется квадратной матрицей порядка n . |
|||
Определение: Числа, из которых состоит матрица, называют ее элементами. |
||||
Для записи матрицы в общем виде используют символ A |
|
, где |
i указывает |
|
aij |
||||
|
|
|
|
|
номер строки, j – номер столбца, в которых содержится элемент.
Определение: Матрицы A и B размеров m n называются равными, если равны их
соответствующие элементы, то есть aij bij , для всех i 1, m ; j 1, n .
Определение: Суммой матриц A и B размеров m n называется матрица C
размеров m |
n , |
каждый элемент которой определяется равенством: cij aij bij для |
||||
|
|
|
|
|
|
|
всех i 1, m; |
j |
1, n . |
||||
Сложение матриц имеет обратную операцию – вычитание, то есть для каждой из
матриц A и B размеров m n существует единственная |
матрица C |
размера |
m |
n |
||||||||||
такая, |
что |
B |
A |
C . |
Матрица |
C |
называется разностью матриц |
A |
и |
B |
||||
обозначается следующим образом: C A |
B . |
|
|
|
|
|
|
|
||||||
Определение: |
Произведением матрицы |
A |
размера |
m |
n на число |
называется |
||||||||
матрица C размера m |
n , элементы которой получены умножением соответствующих |
|||||||||||||
элементов aij на число . |
|
|
|
|
|
|
|
|
|
|
||||
Определение: Произведением матрицы |
A |
размера |
m |
l на матрицу B |
размера |
|||||||||
l n называется матрица C размера m n , каждый элемент Cij |
которой |
равен |
||||||||||||
произведению i |
- й |
строки |
матрицы |
A |
на |
j - й |
столбец матрицы B , |
то есть |
||||||
cij ai1b1 j |
ai 2b2 j |
... |
|
ail blj . |
|
|
|
|
|
|
|
|
|
|
Операция умножения обладает свойствами:
1) A 
B B 
A ;
2) (A B)C A(B C) ;
3) (A B) 
C A 
C B 
C .
Операция умножения матриц соответствующим образом распространяется на случай нескольких сомножителей. В силу определения произведения матриц умножать матрицу A на себя можно только в том случае, если она является квадратной.
5
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
|
1 |
0 ... |
0 |
0 |
|
Определение: Квадратная матрица порядка n E |
0 |
1 ... |
0 |
0 |
, у которой |
|
... ... ... |
... ... |
|
||
|
0 |
0 ... |
0 |
1 |
|
элементы aii 1 для всех i 1, n , а остальные равны нулю, называется единичной
матрицей порядка n .
Определение: Транспонированием матрицы A называется перемена ролями строк и столбцов с сохранением их номеров.
Транспонированную матрицу принято обозначать символом AT . Укажем свойства операции транспонирования:
1) |
AT |
T |
A ; |
|
|
|
|
|
|
|
|
|
|
|
|||
2) |
A B T |
AT |
BT ; |
|
|
|
|
|
3) ( A B)T |
AT |
BT ; |
|
|
|
|
||
4) |
( A)T |
AT , где |
постоянная величина; |
|||||
5) |
AB T |
BT AT . |
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание |
|
Транспонировать матрицу A |
1 |
4 |
3 . |
|||||
|
|
|
|
|
|
1 |
5 |
6 |
|
|
|
|
|
|
|
Решение |
|
|
|
1 |
1 |
|
|
|
|
|
AT |
|
4 |
5 . |
|
|
|
|
|
|
|
3 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание |
|
|
|
|
|
|
|||
|
|
|
|
|
|
3 |
1 |
4 , |
|
1 |
3 |
0 |
0 |
|
|
|
|
|
Найти A B , если A |
B |
1 |
2 |
0 |
0 . |
|
|
|
|
|||||||||
|
|
|
|
|
|
2 |
0 |
5 |
|
0 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
Решение |
|
|
|
|
|
|
|||
|
|
3 |
1 |
4 |
1 |
3 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
. A B |
1 |
2 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
||||
2 |
0 |
5 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
0 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3 1 |
1 1 |
4 0 |
3 3 |
1 2 |
4 0 |
3 0 |
1 0 |
4 1 |
3 0 |
1 0 |
4 1 |
4 |
11 |
4 |
4 . |
|
||
2 1 |
0 1 |
5 0 |
2 3 |
|
0 2 |
5 0 |
2 0 |
0 0 |
5 1 |
2 0 |
0 0 |
5 1 |
2 |
6 |
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
Задание |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
2 |
Найти значение матричного многочлена 2A2 3A |
5E при A |
1 |
3 |
1 , если E – |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
1 |
единичная матрица третьего порядка.
Решение
.
6
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
|
1 |
1 |
2 |
1 |
1 |
2 |
|
10 |
6 |
|
5 |
|
A2 |
1 |
3 |
1 |
1 |
3 |
1 |
|
8 |
11 |
|
6 |
, |
|
4 |
1 |
1 |
4 |
1 |
1 |
|
9 |
8 |
10 |
|
|
|
|
20 |
12 |
10 |
|
|
|
3 |
3 |
6 |
|
|
2 A2 |
|
16 22 12 , 3A 3 9 3 |
, |
|
||||||||
|
|
18 |
16 |
20 |
|
|
12 |
3 |
3 |
|
|
|
|
|
|
1 |
0 |
0 |
|
5 |
0 |
0 |
|
|
|
|
5E |
5 |
0 |
1 |
0 |
|
0 |
5 |
0 , |
|
|
|
|
|
|
0 |
0 |
1 |
|
0 |
0 |
5 |
|
|
|
|
28 |
15 |
16 |
|
|
|
|
|
|
2 A2 3A 5E 19 36 15 . |
|
|
|
|
|
|
|||
|
30 |
19 |
28 |
|
|
|
|
|
|
ВОПРОСЫ ЗАДАНИЙ |
|
|
|
|
|
|
|||
3 |
1 |
0 |
6 |
8 |
1 |
|
4 |
1 |
2 |
1) Найти 3A 2B 6C BT , если A 2 |
0 |
1 ; B |
1 |
0 |
4 |
; C |
0 |
1 |
0 . |
2 |
0 |
5 |
3 |
1 |
2 |
|
2 |
5 |
1 |
|
|
|
|
1 |
0 |
3 |
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2) |
Найти A B |
, если A |
; B |
|
1 |
|
4 . |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
1 |
1 |
1 |
|
|
4 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
1 |
2 |
3 |
1 |
|
|
7 |
5 |
0 |
|
|
1 |
2 |
6 |
|
|
|
|
|
|
|
|
|
|
1 |
2 |
8 |
|
|
|
|
|||||||
3) |
Найти A B |
C CT , если A |
|
7 |
4 |
1 |
2 ; B |
; C |
|
5 |
1 |
2 . |
|
|
|||||||
|
|
|
|
|
|
3 |
1 |
1 |
3 |
|
|
3 |
1 |
2 |
|
|
4 |
3 |
1 |
|
|
|
|
|
|
|
|
|
|
2 |
0 |
1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
3 |
4 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4) |
Найти 2A2 |
A3 |
2E , где A |
0 |
1 |
4 . |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
6 |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
0 |
|
|
6 |
8 |
1 |
|
4 |
1 |
2 |
5) |
Найти 2A |
B |
5C |
BT , если A |
|
2 |
0 |
|
1 ; B |
|
1 |
0 |
4 ;C |
0 |
1 |
2 . |
|||||
|
|
|
|
|
|
|
|
|
2 |
0 |
|
4 |
|
|
3 |
1 |
1 |
|
2 |
5 |
1 |
|
|
|
|
1 |
|
0 |
3 |
|
|
|
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
6) |
Найти A B |
, если A |
|
; B |
|
|
1 |
5 . |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
2 |
|
1 |
1 |
|
|
|
4 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
7
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
|
|
|
0 |
2 |
3 |
1 |
|
7 |
5 |
0 |
|
1 |
2 |
6 |
|
|
|
|
|
1 |
2 |
1 |
|
|
|||||||
7) |
Найти A B |
C CT , если A |
7 |
3 |
1 |
2 ; B |
;C |
5 |
1 |
3 . |
|
||||
|
|
|
3 |
1 |
1 |
1 |
|
3 |
1 |
2 |
|
4 |
3 |
1 |
|
|
|
|
|
2 |
5 |
1 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
2 |
3 |
1 |
|
7 |
5 |
0 |
|
1 |
2 |
6 |
|
|
|
|
|
1 |
4 |
8 |
|
|||||||
8) |
Найти 2A B 3C CT , если A |
7 |
4 |
1 |
2 ; B |
;C |
5 |
1 |
2 . |
||||||
|
|
|
|
3 |
1 |
1 |
3 |
|
3 |
1 |
2 |
|
4 |
3 |
1 |
|
|
|
|
|
2 |
1 |
1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
3 |
4 |
1 |
|
|
|
|
|
|
|
|
|
|
9) |
Найти A2 |
2A3 E , где A |
1 |
0 |
4 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
4 |
9 |
|
|
|
|
|
|
|
|
|
|
|
10) Найти 2A2 |
E , где A 0 |
1 |
4 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
2 |
7 |
|
|
|
|
|
|
|
|
|
|
|
1. 1.2 Разложение определителя по строке или столбцу. Вычисление определителей высших порядков. Обратная матрица
|
|
|
|
Теоретический материал |
|
|
|
|
Рассмотрим квадратную матрицу |
A второго порядка A |
a11 |
a12 . |
|
||||
|
|
|
|
|
|
a21 |
a22 |
|
Определение: Определителем второго порядка, соответствующим |
матрице A , |
|||||||
называется число: a11a22 |
a21a12 , |
которое обозначается |
одним |
из символов |
||||
det A |
a11 |
a12 |
a11a22 |
a21a12 . |
|
|
|
|
a21 |
a22 |
|
|
|
|
|||
|
|
|
|
|
|
|
||
Укажем основные свойства определителя:
1) определитель квадратной матрицы A равен определителю ее транспонированной матрицы AT ;
2)при перестановке столбцов (или строк) определитель изменит знак на противоположный;
3)если все элементы столбца (или строки) равны нулю, то определитель равен
нулю;
4)определитель, имеющий два одинаковых столбца (или строки), равен нулю;
5)если все элементы одного столбца (или строки) определителя умножить на одно и
то же число , то определитель изменится в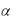 
раз;
6)определитель, у которого элементы двух столбцов (или строк) соответственно пропорциональны, равен нулю;
7)определитель не изменится, если к элементам какого-либо столбца (или строки) прибавить соответствующие элементы другого столбца (или строки), умноженные на одно и то же число.
Рассмотрим квадратную матрицу третьего порядка
8
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
a11 |
a12 |
a13 |
A a21 |
a22 |
a23 . |
a31 |
a32 |
a33 |
Определение: Определителем третьего порядка, соответствующим матрице (А), называется число
a |
a22 |
a23 |
a |
|
a12 |
a13 |
a |
|
a12 |
a13 |
. |
11 |
a32 |
a33 |
|
21 |
a32 |
a33 |
|
31 |
a22 |
a23 |
|
Определение: Минором любого элемента определителя третьего порядка называется определитель второго порядка, соответствующий матрице, полученной из данной матрицы вычеркиванием строки и столбца, на пересечении которых находится выбранный элемент.
Минор элемента aij принято обозначать M ij .
Определение: Алгебраическим дополнением элемента aij определителя третьего
порядка называется минор |
этого |
элемента M ij , умноженный на ( 1)i j , который |
|||
обозначается символом |
A |
( 1)i j |
M |
ij |
. |
|
ij |
|
|
|
|
Теорема: Определитель равен сумме произведений элементов любого его столбца
(или строки) на соответствующие им алгебраические дополнения. |
|
|
|||||||
Определение: Обратной к квадратной |
матрице |
A |
называется матрица |
того |
же |
||||
порядка, удовлетворяющая соотношению: |
AA 1 |
A 1 |
A |
E . |
|
|
|||
Обратная матрица обладает следующими свойствами: |
|
|
|
||||||
1) |
A 1 |
1 |
A ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2) |
( AB) 1 |
B 1 A 1 ; |
|
|
|
|
|
|
|
3) ( AT ) 1 |
( A 1 )T . |
|
|
|
|
|
|
||
Определение: Квадратная матрица |
A |
называется вырожденной, |
если |
ее |
|||||
определитель равен нулю, в противном случае матрицу называют невырожденной. Теорема: Для любой невырожденной матрицы существует обратная, определяемая
равенством:
|
|
|
A11 |
|
A21 |
... |
|
An1 |
|
||
|
|
|
A12 |
|
A22 |
|
An2 |
|
|||
|
1 |
|
|
|
... |
|
|
||||
A |
|
|
|
|
|
|
|
. |
|||
|
|
|
|
|
|
|
|
|
|
||
|
... ... ... ... |
|
|||||||||
|
|
|
A1n |
|
A2n |
|
|
... |
|
Ann |
|
|
|
|
|
|
|
|
|
|
|
||
Определение: Рангом матрицы A размера m n называется наивысший порядок отличных от нуля миноров матрицы A .
Задание
2 4 6
Найти определитель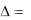 
5 12 19 . 3 9 17
9
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение |
|
|
||
|
19 |
|
5 |
19 |
|
|
5 |
12 |
|
|
|
|
|||||||
2 |
12 |
4 |
|
6 |
|
2 12 17 |
9 19 |
|
|||||||||||
|
9 |
17 |
|
3 |
17 |
|
|
3 |
|
9 |
|
|
|
|
|
|
|
||
4 5 17 |
3 19 |
|
6 5 9 |
3 12 |
|
2(204 |
171) |
4(85 |
57) |
||||||||||
|
6(45 |
36) |
|
2 33 |
4 28 |
6 9 |
66 |
112 |
54 |
8 . |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
0 |
1 |
|
Найти определитель матрицы A |
|
2 |
1 |
3 |
4 . |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
2 |
1 |
0 |
|
Решение
Разложим данный определитель по элементам его третьего столбца.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
4 |
|
|
|
|
|
|
|
|
|
2 |
2 |
1 |
|
|
|
|
|
|
|
A |
|
a A a |
23 |
A a |
|
A a |
43 |
A |
|
1 1 3 0 |
1 1 2 |
|
|
1 2 3 3 |
1 1 2 |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
13 |
|
13 |
|
|
|
|
23 |
|
|
|
33 |
|
33 |
|
43 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
2 |
0 |
|
|
|
|
|
|
|
|
|
5 |
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
1 3 |
3 |
0 |
|
2 |
|
1 |
4 |
|
|
|
|
|
|
1 4 |
3 |
1 |
|
2 |
1 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
5 |
|
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
3 (0 2 |
20 |
5 |
|
8 |
|
0) |
|
1 (4 |
2 |
|
8 1 |
8 |
8) |
|
3 9 |
1 ( |
3) |
|
24 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Дана матрица A |
|
1 |
|
|
|
3 |
|
1 |
. Найти обратную матрицу. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
3 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Вычислим определитель матрицы A : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
|
3 |
|
|
1 |
|
|
27 |
2 |
|
|
24 |
5 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
5 |
|
3 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Находим алгебраические дополнения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
A11 |
|
|
1 |
|
|
|
9 , A21 |
|
|
|
2 |
2 |
|
|
2 , |
A31 |
|
2 |
2 |
|
|
4 , A12 |
|
1 |
|
1 |
|
1 |
, |
A22 |
|
3 |
2 |
|
2 |
, |
||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
3 |
|
4 |
|
|
|
|
|
|
3 |
4 |
|
|
|
3 |
1 |
|
|
|
5 |
|
4 |
|
|
5 |
4 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
A32 |
|
|
|
|
|
2 |
|
|
|
|
1, A13 |
|
1 |
|
3 |
|
12 , A23 |
|
3 |
2 |
|
1 |
, A33 |
|
3 |
2 |
|
7 . |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
1 |
|
1 |
|
|
|
|
|
5 |
|
3 |
|
|
5 |
3 |
|
|
|
1 |
3 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
10
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
|
9 / 5 |
|
2 / 5 |
|
4 / 5 |
Следовательно, A 1 |
1/ 5 |
2 / 5 |
|
1/ 5 . |
|
|
12 / 5 |
1/ 5 |
|
7 / 5 |
|
|
|
|
Задание |
||
|
3 |
1 |
1 |
2 |
8 |
Найти ранг матрицы A |
7 |
1 |
2 |
1 |
12 . |
|
11 |
1 |
3 |
0 |
16 |
|
10 |
2 |
3 |
3 |
20 |
Решение
После вычитания первой строки из остальных получаем эквивалентную матрицу
|
3 |
1 |
1 |
2 |
8 |
|
|
|
|
|
|
A ~ |
4 |
0 |
1 |
1 |
4 |
~ |
3 |
1 |
1 |
2 |
8 . |
|
8 |
0 |
2 |
2 |
8 |
|
4 |
0 |
1 |
1 |
4 |
|
4 |
0 |
1 |
1 |
4 |
|
|
|
|
|
|
Поскольку три строки промежуточной матрицы были пропорциональны, то из них можно получить две нулевые строки, которые можно отбросить. Так как,
M 2 |
3 |
1 |
4 , то RangA |
2 . |
|
|
|
|
|
|
|
|
4 |
0 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
ВОПРОСЫ ЗАДАНИЙ |
|||||||
|
|
|
|
|
|
4 |
6 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||
1) |
Найти определитель |
|
|
5 |
11 |
15 |
. |
|
|
|
||
|
|
|
|
|
|
1 |
6 |
13 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
0 |
1 |
|
2) |
Найти определитель матрицы A |
2 |
1 |
3 |
4 . |
|||||||
|
|
|
|
|
|
|
|
1 |
3 |
1 |
2 |
|
|
|
|
|
|
|
|
|
5 |
2 |
4 |
1 |
|
|
|
|
5 |
1 |
2 |
|
|
|
|
|
|
|
3) |
Дана матрица A 1 |
3 |
7 |
. Найти обратную матрицу. |
||||||||
|
|
|
5 |
2 |
4 |
|
|
|
|
|
|
|
|
3 |
1 |
1 |
2 |
8 |
4) Найти ранг матрицы A |
7 |
1 |
2 |
1 |
12 . |
|
11 |
1 |
3 |
0 |
16 |
|
10 |
2 |
3 |
3 |
20 |
11