
новая папка 1 / 278642
.pdf
Для определения доверительного интервала необходимо задаться доверительной вероятностью, затем для данной вероятности определить квантиль нормированного распределения Лапласа [1]. . Результат эксперимента запишется в виде:
|
|
x |
x |
z0,5P S |
x |
. |
|
|
|
(15) |
|
Таблица 4 – Значения |
и P |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
II 0,01 |
II |
0,02 |
II |
0,05 |
|||||
|
|
|
|
||||||||
10 |
1 |
|
0,98 |
|
|
|
0,98 |
|
0,96 |
||
|
|
|
|
|
|
|
|
|
|
||
11 – 14 |
1 |
|
0,99 |
|
|
|
0,98 |
|
0,97 |
||
|
|
|
|
|
|
|
|
|
|
||
15 – 20 |
1 |
|
0,99 |
|
|
|
0,99 |
|
0,98 |
||
|
|
|
|
|
|
|
|
|
|
||
21, 22 |
2 |
|
0,98 |
|
|
|
0,97 |
|
0,96 |
||
|
|
|
|
|
|
|
|
|
|
||
23 – 27 |
2 |
|
0,98 |
|
|
|
0,98 |
|
0,97 |
||
|
|
|
|
|
|
|
|
|
|
||
28 – 32 |
2 |
|
0,99 |
|
|
|
0,98 |
|
0,97 |
||
|
|
|
|
|
|
|
|
|
|
||
33 – 35 |
2 |
|
0,99 |
|
|
|
0,98 |
|
0,98 |
||
|
|
|
|
|
|
|
|
|
|
||
36 – 49 |
2 |
|
0,99 |
|
|
|
0,99 |
|
0,98 |
||
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 5 – Верхняя квантиль нормированного распределения Лапласа
P |
0,90 |
0,95 |
0,96 |
0,97 |
0,98 |
0,99 |
|
|
|
|
|
|
|
z0,5P |
1,65 |
1,96 |
2,06 |
2,17 |
2,33 |
2,58 |
11
2 Пример выполнения лабораторной работы
Имеем ряд результатов измерений прогиба балки (записанных в микрометрах), полученный с помощью индикатора перемещений часового типа: 2490, 2460, 2470, 2540, 2470, 2290, 2500, 2520, 2370, 2430, 2550, 2460, 2470, 2480, 2470, 2970, 2480, 2500, 2540, 2450, 2610, 2000, 2650, 2470.
Расположим данный ряд в порядке возрастания, присвоив каждому значению порядковый номер. Полученный вариационный ряд представим в виде таблицы 6.
Таблица 6 – Вариационный ряд
х1 |
х2 |
х3 |
х4 |
х5 |
х6 |
х7 |
х8 |
х9 |
х10 |
х11 |
х12 |
|
2000 |
2290 |
2370 |
2430 |
2450 |
2460 |
2460 |
2470 |
2470 |
2470 |
2470 |
2470 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х13 |
х14 |
х15 |
х16 |
х17 |
х18 |
х19 |
х20 |
х21 |
х22 |
х23 |
х24 |
|
2480 |
2480 |
2490 |
2500 |
2500 |
2520 |
2540 |
2540 |
2550 |
2610 |
2650 |
2970 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Количество результатов эксперимента: n=24. |
|
|
|
|
|||||||
|
Среднее арифметическое |
х |
результатов эксперимента: |
|
|
|
||||||
х1 n xi =2485 мкм. ni 1
Дисперсия:
|
1 |
|
n |
|||
|
|
(xi |
x |
)2 =159,2 мкм. |
||
n 1 |
||||||
|
i 1 |
|||||
|
|
|
||||
Проведем проверку на наличие промахов по критерию 3 .
Подозрительными результатами измерения являются результаты, наиболее удаленные от среднего арифметического (х1 и х24 ). Проверяем х1:
x1 x 2000 2485 485мкм; 3 3 159,2 477,6мкм.
Так как 485 477,6, следовательно, х1 является промахом и исключается из
вариационного ряда.
12
Вычисляем среднее арифметическое и дисперсию для нового вариационного ряда, включающего 23 результата эксперимента:
х 2506,1 мкм, 123,9 мкм.
Проверяем х24 :
x24 x 2970 2506,1 463,9мкм; 3 3 123,9 371,7мкм.
Так как 463,9 371,7, следовательно, х24 является промахом и исключается из вариационного ряда.
Проверим х2 и х23. Вычисляем среднее арифметическое и дисперсию для нового вариационного ряда, включающего 22 результата эксперимента:
х 2485 мкм, 73,3 мкм.
x2 x 2290 2485 195мкм; 3 3 73,3 219,9мкм.
Так как 195 219,9, следовательно, х2 не является промахом. x23 x 2650 2485 165мкм.
Так как 165 219,9, следовательно, х23 также не является промахом.
Проведем проверку на наличие промахов по критерию Романовского. При проведении проверки зададимся вероятностью 0,05. Проверяем х1. По таблице 1
определим для значения n=24 квантиль распределения Стьюдента t=2,112:
x1 x 2000 2485 485мкм; t 2,112 159,2 336,2мкм.
Так как 485 336,2, следовательно, х1 является промахом и исключается из вариационного ряда.
Вычисляем среднее арифметическое и дисперсию для нового вариационного ряда, включающего 23 результата эксперимента, определяем квантиль распределения:
х 2506,1 мкм; 123,9 мкм; t=2,119.
Проверяем х24 :
x24 x 2970 2506,1 463,9мкм; t 2,119 123,9 262,5мкм.
Так как 463,9 262,5, следовательно, х24 является промахом и
исключается из вариационного ряда.
13

Проверим х2:
х 2485 мкм, 73,3 мкм, t=2,127 (для n=22).
x2 x 2290 2485 195мкм; t 2,127 73,3 155,9мкм.
Так как 195 155,9, следовательно, х2 - промах.
Проверим х23:
х 2494,3 мкм, 60,4 мкм, t=2,135 (для n=21).
x23 x 2650 2494,3 155,7мкм; t 2,135 60,4 129мкм.
Так как 155,7 129, следовательно, х23 - промах.
Проверим х3:
х 2486,5 мкм, 50 мкм, t=2,145 (для n=20).
|
x3 |
x |
|
2370 2486,5 |
116,5мкм; t |
2,145 50 107,3мкм. |
Так как 116,5 107,3, следовательно, |
х3 - промах. |
|||||
Проверим х22 :
х 2492,6 мкм, 42,9 мкм, t=2,156 (для n=19).
x22 x 2610 2492,6 117,4мкм; t 2,156 42,9 92,3мкм.
Так как 117,4 92,3, следовательно, х22 - промах.
Проверим х4:
х 2486,1 мкм, 33,1 мкм, t=2,168 (для n=18).
x4 x 2430 2486,1 56,1мкм; t 2,168 33,1 71,8мкм.
Так как 56,1 71,8, следовательно, х4 не является промахом.
Проверим х21:
x21 x 2550 2486,1 63,9мкм; t 2,168 33,1 71,8мкм.
Так как 63,9 71,8, следовательно, х21 не является промахом.
Оценка среднего квадратичного отклонения среднего арифметического:
S |
x |
|
|
|
|
33,1 |
|
7,8мкм. |
|
|
18 |
|
|||||
|
|
|
n |
|
|
|||
Вариационный ряд без промахов представим в таблице 7.
14

Таблица 7 – Вариационный ряд без промахов
х1 |
х2 |
х3 |
х4 |
х5 |
х6 |
х7 |
х8 |
х9 |
2430 |
2450 |
2460 |
2460 |
2470 |
2470 |
2470 |
2470 |
2470 |
|
|
|
|
|
|
|
|
|
х10 |
х11 |
х12 |
х13 |
х14 |
х15 |
х16 |
х17 |
х18 |
2480 |
2480 |
2490 |
2500 |
2500 |
2520 |
2540 |
2540 |
2550 |
|
|
|
|
|
|
|
|
|
Разобьем вариационный ряд на интервалы. Количество интервалов:
m 1 3,31 lg18 5,15 5.
Ширина интервала:
l xmax xmin 2550 2430 24 мкм. m 5
Используя формулы (8), (9) и (10), определим границы интервалов, средние значения интервалов, частоты попадания и статистическую вероятность попадания в интервал. Результаты представим в таблице 8, на основании полученных данных построим гистограмму результатов эксперимента.
Таблица 8 – Промежуточные значения интервального ряда
Номер |
Границы |
Среднее |
Частота |
Статистическая |
интервала |
интервала |
значение |
попадания в |
вероятность |
|
xmin k xmaxk |
интервала |
интервал |
Pk |
|
|
xk0 |
vk |
|
1 |
2430 – 2454 |
2442 |
2 |
0,11 |
|
|
|
|
|
2 |
2454 – 2478 |
2466 |
7 |
0,39 |
|
|
|
|
|
3 |
2478 – 2502 |
2490 |
5 |
0,28 |
|
|
|
|
|
4 |
2502 – 2526 |
2514 |
1 |
0,05 |
|
|
|
|
|
5 |
2526 – 2550 |
2538 |
3 |
0,17 |
|
|
|
|
|
15
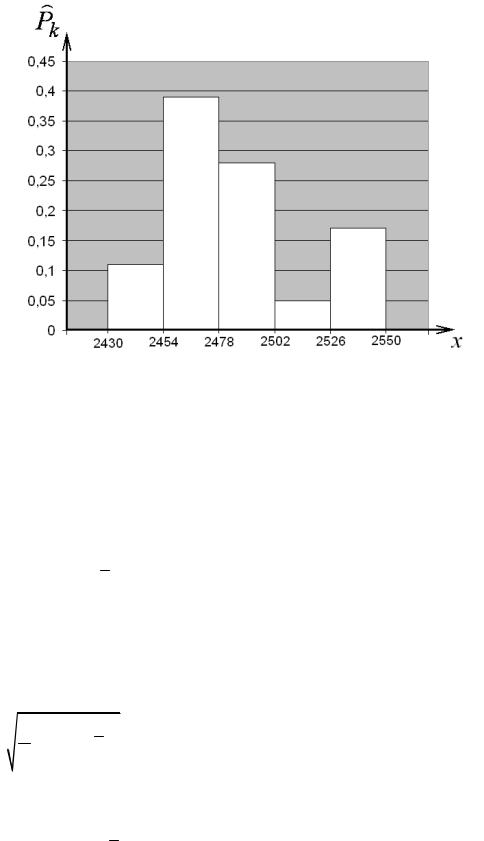
Рисунок 1 – Гистограмма результатов эксперимента
Из рисунка 1 видно, что гистограмма имеет вид, близкий к колоколообразному. Это свидетельствует о возможности принадлежности распределения экспериментальных данных нормальному закону.
Проверим нормальность распределения результатов эксперимента по
составному критерию d . Принимая уровни значимости по критериям I 0,02 и
II 0,02, определим уровень значимости по составному критерию:
I II 0,04.
Смещенная оценка среднего квадратичного отклонения:
* 
 1n n (xi x)2 =32,2 мкм.
1n n (xi x)2 =32,2 мкм.
i1
Критерий:
|
|
|
1 |
|
m |
||||||
|
|
|
|
|
|
xk0 |
|
|
|
vk =0,745. |
|
d |
|
|
x |
|
|||||||
n |
* |
||||||||||
|
|
|
|
k 1 |
|||||||
16

Имеем n=18, из таблицы 3 находим для |
n=16: d0,01 0,9137, |
d0,99 0,6829; для n=21: d0,01 0,9001, d0,99 0,695. Следовательно, для n=18:
d0,01 0,9137 0,9137 0,9001 2 0,9083, 5
d0,99 0,6829 0,695 0,6829 2 0,6877. 5
Так как 0,6877 0,745 0,9083, следовательно, гипотеза о нормальном распределении по критерию I для заданного уровня значимости подтверждается.
Проверяем выполнение критерия II. По таблице 4 для n=18 и II 0,02
определяем: =1, P=0,99. Из таблицы 5 находим z0,5P =2,58.
Тогда z0,5P =85,4 мкм.
x10 x =|2442-2486,1|=44,1мкм < 85,4 мкм. x50 x =|2538-2486,1|=51,9мкм < 85,4 мкм.
Ни одна из разностей не превышает значение z0,5P , следовательно,
гипотеза о нормальности распределения подтверждается по обоим критериям для принятого уровня значимости.
Зададимся доверительной вероятностью P=0,95, затем для данной вероятности по таблице 5 определим квантиль нормированного распределения Лапласа z0,5P =1,96. Результат эксперимента:
x x z0,5P Sx 2486,1 1,96 7,8 мкм, x 2486,1 15,3 мкм.
17
Список использованных источников
1 Основы научных исследований: методическое пособие для студентов-
магистрантов/ под ред. В. Н. Евсюкова. – Оренбург: ИПК ГОУ ОГУ, 2011. – 316 с. 2 Третьяк, Л.Н. Обработка результатов наблюдений: учебное пособие /
Л.Н. Третьяк. – Оренбург: ГОУ ОГУ, 2004. – 171 с.
3 Метрология и радиоизмерения. Статистическая теория погрешностей измерения. Методы статистической обработки: учебно-методическое пособие к самостоятельной работе студентов специальностей 210302.65 «Радиотехника», 210301.65 «Радиофизика», 210304.65 «Радиоэлектронные системы»; направления
210300.62 «Радиотехника» / сост. А.М. Алешечкин. – Красноярск: Сиб. федер.
ун-т, 2012. – 49 с.
4 Новицкий, П.В. Оценка погрешностей результатов измерений / П.В.
Новицкий, И.А. Зограф. – М : Энергоатомиздат, 1985. – 248 с.
5 Колоколов, С.Б. Основы научных исследований: учебное пособие / С.Б.
Колоколов. – Оренбург: ИПК ГОУ ОГУ, 2008. - 115 с.
18
