2546

цифровых фильтров с одновременно заданными произвольными АЧХ и ФЧХ (ГВЗ), а также в ряде других случаев задача НЛП (3.1) очень часто формулируется как нелинейная минимаксная [37]:

фиксированный набор индексов. В дальнейшем будем пользоваться также понятиями набора

-активных функций и ограничений [21]:

где

F ( X ) max max gi ( X ),0 .

i 1:P

Так же, как и при решении гладкой задачи НЛП (3.1.), существуют два подхода для учета ограничений в задаче (3.24). В первом исходная задача преобразуется к безусловной путем добавления к целевой функции некоторой скалярной функции штрафа, зависящей от функций ограничений и параметров (метод штрафных функций). При этом решается последовательность задач безусловной оптимизации, в промежутках между которыми выполняется коррекция параметров штрафной функции (коэффициентов штрафа). Другой подход основывается на непосредственном учете ограничений: стратегии набора активных ограничений и необходимых условий оптимальности. В дальнейшем при решении нелинейной минимаксной задачи для учета ограничений будем использовать, как и в п.3.2

стратегию набора активных ограничений и необходимых условий оптимальности.

В зависимости от степени учета структуры и особенностей функции максимума Q(X )

можно выделить несколько групп методов, которые можно использовать для решения задачи

(3.24): методы сглаживания функции максимума (МСФМ) [11]; методы обобщенного градиентного спуска (ОГС) [99] или 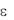- субградиента; методы 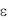- наискорейшего спуска

(МНС) [25]; методы выравнивания максимумов (МВМ) [48, 90]; методы возможных направлений (МВН) [28, 48, 69 - 71]; комбинированные методы (КМ) [54, 67].

124

В МСФМ негладкая функция Q(X ) аппроксимируется некоторой гладкой целевой функцией, которая затем минимизируется одним из подходящих методов оптимизации. Эти методы аналогичны методу штрафных функций со всеми свойственными ему недостатками.

Наиболее часто в качестве сглаженной целевой функции используется среднестепенной критерий (2.14) при больших степенях q, либо его модификации (2.15), (2.22). Для минимизации критериев (2.14), (2.15) и (2.22) в данной работе применяется алгоритмы,

рассмотренные в п.3.1 и п.3.2 данной главы. Сглаженная целевая функция, как правило, хуже учитывает свойства функции максимума Q(X) и имеет достаточно сложный "овражный"

характер. Поэтому в алгоритмах данной группы многое зависит от эффективности и

надежности используемых алгоритмов.

МСФМ являются наиболее простыми при решении задачи (3.24), однако вычислительный опыт показывает [54], что алгоритмы, построенные на основе методов этой группы являются очень трудоемкими по числу оценок целевой функции и достаточно медленно сходятся из-за овражного характера целевой функции. Поэтому наиболее часто эти

алгоритмы используют для решения задач малой и средней размерности.

Методы ОГС или -субградиента предназначены для минимизации выпуклых не дифференцируемых функций общего вида и слабо учитывают структуру функции максимума. Методы -субградиента, с одной стороны, близки к МНС [21], а с другой стороны, в формальном отношении примыкают к методам сопряженных направлений.

Однако скорость сходимости методов этой группы весьма низкая, и в лучшем случае является линейной. Методы ОГС не отличаются свойствами релаксационности, но просты в реализации, экономичны в вычислениях и имеют хорошую скорость сходимости. В этих

методах итерационный процесс осуществляется по следующей формуле:

точке минимума X*, чем точка Xk, т. е. ||Xk+1 – Xk|| < ||Xk+1 – X*||. Данный метод выигрывает в

125

простоте, но проигрывает за счет этого в скорости сходимости. По этой причине метод ОГС в данной работе не используется для решения нелинейных минимаксных.

В МНС минимум функции Q( X ) max Qi ( X ) ищется с помощью итерационного

i

процесса типа (3.7) [21]. Шаг k определяется путем одномерного поиска, а вектор спуска

G(k ) находится из решения следующей вспомогательной задачи. Для малого фиксированного

i

минимума, то L(Xk) не содержит начала координат, и вектор G(k ) , исходящий из Xk,

направленный на ближайшую точку L(Xk) и взятый со знаком минус, указывает направление наискорейшего убывания функции Q(X ) в точке Xk. Описанный метод аналогичен методу наискорейшего спуска для гладких функций и характеризуется всеми его недостатками и достоинствами.

После шага в направлении наискорейшего спуска часто бывает полезным возвратится на поверхность равных максимумов задачи (3.24) Для этой цели используется МВМ [48]. В

итерации определяется из решения задачи линейного программирования (ЛП) [4, 69 - 71] min Z

126

где сj - вектор коэффициентов; bj - скалярный коэффициент линейных ограничений,

задающих область допустимых значений D.

Шаг вдоль найденного направления G(k ) определяется с помощью одномерного поиска.

Метод вырабатывает последовательность значений {Zk} 0. Условие Zk = 0 эквивалентно

необходимому условию минимакса [71], однако на практике, как правило, ограничиваются условием |Zk| 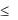0, где 0 - требуемая точность решения. Однако вычислительный опыт автора свидетельствует, что МВН, так же, как и другие ранее рассмотренные методы,

обладает малой скоростью сходимости при решении задачи оптимизации УЦОС (3.24).

Анализ показал, что причиной плохой сходимости рассмотренных методов является существенная «овражность» целевой функции (3.24). Одной из причин существенной овражности является плохая масштабированность вектора варьируемых параметров.

При неоднородности варьируемых параметров меньшие составляющие градиентов в градиентных методах фактически нивелируются в процессе формирования направления поиска. Поэтому эти методы решения задачи НЛП при оптимизации УЦОС становятся либо алгоритмически ненадежными, либо скорость их сходимости уменьшается, так как меньшие составляющие градиентов являются определяющими при формировании направления

поиска.

Для преодоления указанных выше трудностей предлагается перед формированием

В ряде случае исходное пространство переменных целесообразно преобразовать в пространство логарифмических переменных. В преобразованном пространстве новые

переменные определяются по формуле

где Ki - нормализующий коэффициент.

В условиях неоднородности управляемых переменных для ускорения сходимости рассмотренных выше методов целесообразно производить растяжение пространства по координатным осям, в результате которого выравниваются компоненты векторов градиентов. При этом гиперповерхности функций Qi ( X ) в окрестности точки X

127

приобретают форму, близкую к сферической, а направление наискорейшего спуска грубо, в

первом приближении, указывает на минимум целевой функции.

Во всех рассмотренных методах на протяжении всего процесса минимизации функции Q(X ) применялся один и тот же алгоритм поиска. Вместе с тем характер поведения этой функции существенно меняется на различных этапах поиска. Эту особенность и пытались учесть авторы различных комбинированных методов. Так, в работе [67]

предлагалось в случае одной активной функции использовать метод переменного порядка. В

работе [54] предложено использовать двухэтапную процедуру поиска. На первом этапе происходит движение методом наискорейшего спуска до попадания в окрестность гребня,

образованного пересечением гиперповерхностей нескольких активных функций. Поиск на втором этапе осуществляется в соответствии со стратегией метода проекции вектора-

градиента и требует последовательности выполнения пар шагов. Первый шаг выполняется в сторону гребня, а второй - вдоль него. Этот метод успешно применяется для решения некоторых задач оптимизации электронных схем, однако из-за ряда недостатков вычислительного характера непригоден для решения задач оптимизации УЦОС. Процедура идентификации гребней предусматривает добавление только одной активной функции. На каждой итерации второго этапа дважды выполняется перемножение матриц и дважды решается система линейных уравнений. Если же гребень существенно нелинейный, то перемещение по касательной к нему приведет к тому, что на первом шаге последующей итерации придется неоднократно решать систему линейных уравнений, чтобы снова попасть в -окрестность. Скорость сходимости метода только линейная. В работах [67, 101 - 106]

также рассматриваются двухэтапные методы решения задачи (3.24), однако они также не учитывают особенности и специфику задач оптимального проектирования УЦОС.

Таким образом, качественное исследование существующих методов минимаксной оптимизации показало, что наиболее эффективными являются комбинированные методы,

использующие растяжение пространства по координатным осям для устранения существенной «овражности» ЦФ. В коллектив оптимизирующих алгоритмов для решения задачи (3.24) целесообразно включить методы ВМ и ВН.

3.4 Комбинированный проблемно – адаптивный алгоритм оптимизации

обобщенных критериев оптимальности УЦОС

128

В процессе решения задачи оптимизации (3.1) возникает большое количество не предсказуемых заранее ситуаций. Предсказать эти ситуации на этапе разработки алгоритма оптимизации практически невозможно из за различного субъективного отношения пользователей к способам выхода из этих ситуаций. Совокупность таких ситуаций порождает задачу, относящуюся к трудно формализуемым. Построить жесткий алгоритм решения задачи (3.1) невозможно. Наиболее эффективным средством решения трудно формализуемых задач являются методы и программы искусственного интеллекта (ИИ), в

частности экспертные системы (ЭС). Подходы, используемые в ИИ, позволяют легко учитывать эвристические знания проектировщиков, накопленные ими при решении большого числа практических задач. Однако стандартные ЭС содержат в своем составе большое количество сложных блоков, таких, например, как блок отбора знаний от экспертов,

объясняющий блок и т. д. Быстродействие таких ЭС невелико. В то же время в процессе оптимизации требуется принимать решение либо достаточно быстро, либо оперативно

(сверхбыстро). Следовательно, стандартная ЭС для принятия решений в этих случаях не годится.

Одним из путей построения гибких алгоритмов оптимизации УЦОС может служить проблемно – адаптивный подход, который неоднократно использовался целым рядом автором при решении разноплановых задач оптимального проектирования [32, 60, 75, 81, 97]. Этот подход достаточно целесообразен при построении комбинированных алгоритмов оптимизации УЦОС, так как предполагает наличие коллектива конкурирующих алгоритмов оптимизации, с помощью комбинирования которых можно строить гибкие стратегии оптимизации.

В коллектив оптимизирующих алгоритмов вошли: алгоритм поискового метода (ПМ), использующий ЛПτ-последовательности; алгоритм метода статистического градиента; алгоритм метода деформируемого многогранника; алгоритм метода сопряженных градиентов; модифицированный алгоритм метода ВН; алгоритм метода ВМ;

модифицированный второй алгоритм Е.Я. Ремеза.

На основании результатов качественного исследования методов решения задачи (3.1)

и (3.24), а также на основании опыта решения практических задач оптимизации можно предложить комбинированный проблемно адаптивный алгоритм оптимизации обобщенных критериев оптимальности при оптимальном проектировании УЦОС.

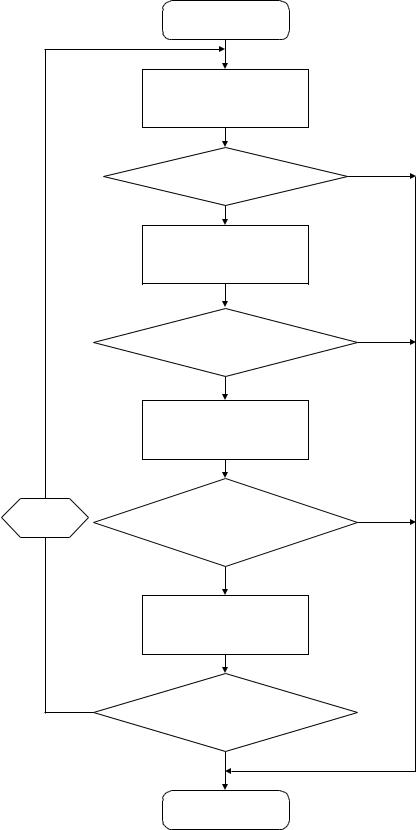
Процедура минимизации с использованием комбинированного проблемно– адаптивного алгоритма включает в себя четыре этапа, приведенные на рис. 3.3.

129

1. Анализ исходной точки с использованием алгоритма ПМ. Осуществляется минимизация среднеквадратичного обобщенного критерия Q(X ) . Алгоритм работает в соответствии с описанием, приведенным в п. 3.1. Процесс изменения размеров области поиска продолжается до тех пор, пока либо ее размеры не превысят размеров области допустимых значений (ОДЗ),

130

либо пока диаметр гиперпараллелепипеда, образованного параметрическими

ограничениями, не станет меньше требуемой точности вычислений. Результат первого этапа

-опорное решение, которое используется на втором этапе.

2.Спуск по статистическому градиенту. Спуск по статистическому градиенту осуществляется по следующей схеме:

а) в точке X(k) рассчитывается направление статистического градиента

..., L 1 , - независимые случайные векторы, равномерно распределенные на сфере заданного радиуса вокруг точки X(k); L1 – число пробных вычислений целевой функции.

б) рассчитывается значение целевой функции Q в точке

остается прежним и процесс повторяется, начиная с пункта а). Если Q( X 2(k 1) ) < Q( X 1(k 1) ) , то

многогранника.

Начальный размер многогранника определяется достигнутым на предыдущем

этапе шагом поиска. В качестве начальной точки берется последняя успешная точка,

полученная в процессе поиска по статистическому градиенту. Точность поиска задается пользователем. Стандартный алгоритм деформируемого многогранника модифицирован путем введения порога аналогично тому, как это сделано в алгоритме ПМ в п. 3.1. Для случая, когда производные конкретного обобщенного критерия вычисляются аналитически,

а размерность вектора X относительно невелика, вместо метода деформируемого многогранника используется метод сопряженных градиентов, алгоритм которого приведен в п. 3.2.

132

Результат третьего этапа - опорное решение, которое используется на четвертом шаге.

4. Минимизация минимаксного критерия. Опорное решение, полученное на третьем этапе, оптимизируется либо с использованием алгоритма метода ВМ, либо - ВН.

Алгоритм метода ВМ используется в том случае, если на третьем этапе найден валле-

пуссеновский альтернанс, в противном случае используется алгоритм метода ВН. Если минимаксный критерий линейный, то на третьем этапе используется модифицированный алгоритм Ремеза.

Общая схема маршрута проектирования приведена на рис. 3.4.

Структурная схема алгоритма Ремеза приведена на рис. 3.5.

Весовые коэффициенты (см. рис. 3.6) в свертке либо задаются пользователем, либо вычислены на основе комбинированного алгоритма, включающего в себя три известных метода: вычисления весовых коэффициентов по коэффициентам относительного разброса ЛКО, на основе теоретико-игровой модели и “энтропийной” модели. В ряде случаев расчет весовых коэффициентов производится путем решения задачи линейного программирования.

Кроме того для расчета весовых коэффициентов использован метод зондирования пространства векторов весовых коэффициентов, основанный на построении ЛП -

последовательностей.

133