m0936

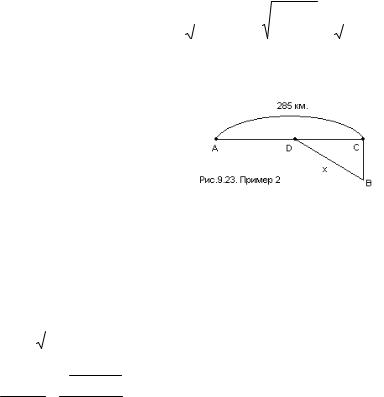
Из условия задачи ясно, что минимального значения площадь принимать не может, так как вписанный прямоугольник можно сделать как угодно узким («горизонтальным» или «вертикальным»). Более того, понятно, что максимальное значение площади обязательно где-то достигается: представим себе достаточно узкий «горизонтальный» прямоугольник, вписанный в эллипс, и будем увеличивать переменную x. При этом, если прямоугольник остается вписанным, величина y будет уменьшаться, и в ка- кой-то момент x y мы получим квадрат. Будем продолжать уменьшать переменную x – прямоугольник, оставаясь вписанным, станет «вертикальным», и площадь его будет уменьшаться, значит, где-то при изменении переменной x мы имели хотя бы одно максимальное значение площади. Проведенные выше вычисления показывают, что максимальное значение площади ров-

t x 285 x x2 602 . 52 20

141

По условию задачи общее время t x должно быть мини-

мальным. Определяем критические точки функции t x :

Читателю предоставляется возможность самостоятельно проверить, что полученное значение действительно является точкой минимума функции t x .

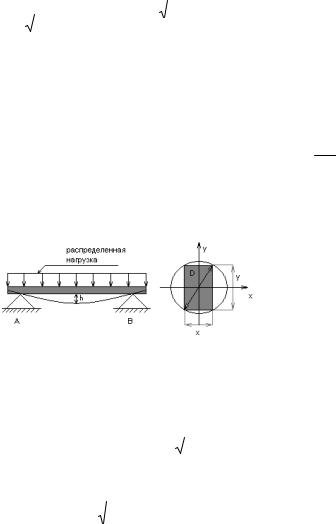
Пример 3. Балка прямоугольного сечения со свободно опертыми концами равномерно нагружена по всей длине (рис. 9.24).

Стрела прогиба h обратно пропорциональна величине J xy3 , 12

где x, y – поперечные размеры балки. Определить значения раз-

меров x, y балки, изготовляемой из бревна диаметра D, чтобы прогиб h балки был минимальным.

Рис. 9.24. Нагруженная балка

Решение. Из курса сопротивления материалов известно, что

Определяем критические точки первого рода, в которых возможен минимум. Для упрощения вычислений используем логарифмическое дифференцирование:

142

D2 4x2 0 x D, y 3 D. 2 2

Проверка. Используем первое достаточное условие экстремума. Из физического смысла задачи следует, что для нагруженной балки всегда h x 0, D x, x 0. Поэтому знак производ-

ной h x зависит только от знака числителя. Используем метод

в точке стационарности x D в соответствии с первым доста- 2

точным условием экстремума имеем минимум.

Задачи к разделу 9.6

9.6.1.Из стального листа размером 2,4 1,5 м2 необходимо изготовить прямоугольную емкость без крышки максимального объема. Найти длину сторон квадратов, вырезаемых в углах стального листа при изготовлении емкости, и ее объем.

9.6.2.Балка со свободно опертыми концами нагружена по всей длине (рис. 9.25) равномерно распределенной нагрузкой интенсивностью

q, Н/м. Найти максимальный прогиб балки, если уравнение изогнутой балки как линии имеет вид:

где l – длина балки, C – некоторая константа.

143

Замечание. В расчетной схеме (см. рис. 9.25) условно показано, что конструкция крепления балки в точке А позволяет ей свободно поворачиваться, а в точке В – поворачиваться и смещаться в горизонтальном направлении.

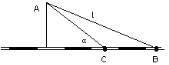
9.6.3.Вблизи завода A проходит железная дорога (рис. 9.26)

кпункту B. Под каким углом необ-

ходимо построить шоссе, чтобы комбинированная доставка изделий с завода A была наиболее дешевой, если

стоимость доставки на один километр

по шоссе в m раз дороже, чем по же- Рис. 9.26. Схема дорог лезной дороге?

9.6.4.Труба для стока воды под железной дорогой имеет в сечении форму прямоугольника с основанием x и высотой h, который завершается сверху полукругом. Определить, при каких значениях x и h площадь сечения будет наибольшей, если периметр сечения равен P.

9.6.5.Сечение тоннеля имеет форму прямоугольника, завершенного сверху полукругом. Периметр сечения – 18 м. При каком радиусе полукруга площадь сечения будет максимальной?

Ответы к задачам темы «Основные свойства функций»

9.2.1. а) Четные: 3, 6, 12; нечетные: 2, 5, 7, 8, 10, 11; б) функция является четной, если ее график симметричен относительно оси ординат; функция является нечетной, если ее график симметричен относительно начала координат; в) многочлен является четной функцией, если он содержит только четные степени переменной (включая, возможно, нулевую степень); многочлен является нечетной функцией, если он содержит только нечетные степени переменной; г) может, но такая функция единственна:

этом равенстве первое слагаемое – четная функция, второе – нечетная.

9.2.2. а) f x nT f x n 1T T f x n 1T

f x n 2 T T ... f x ; б) область значений функции f x должна

144

9.4.2. а) x0 2 – точка минимума; б) x1 3 – точка минимума, x2 5 –

точка максимума; в) x1 3 – точка максимума, x2 1 – точка минимума. 4

145

максимума; г) xn n,n N – точки минимума, xn 2 n,n N – точки

9.5.3.а) 2,09; б) 0,82; в) –0,57.

9.5.4.а) x1 2,60; x2 0,34; x3 2,26; б) x1 0,72; x2 1,22.

Требования к практическому усвоению темы «Основные свойства функций»

Студент должен знать:

–общие свойства функций (непрерывность и гладкость, чет- ность-нечетность, периодичность, ограниченность) и способы их определения;

–частные свойства функций (знакопостоянство, монотонность, выпуклость-вогнутость); способы нахождения интервалов знакопостоянства; определение интервалов возрастания и убыва-

146

ния функций с помощью первых производных; нахождение интервалов выпуклости-вогнутости с помощью вторых производных;

–определения локальных свойств функций (нули функций, экстремумы, перегибы, наибольшие и наименьшие значения функций); геометрические интерпретации локальных свойств функций;

–необходимые и достаточные условия наличия экстремумов

вслучае гладких функций; условия существования «острых» экстремумов у негладких непрерывных функций;

–определение перегиба функции, нахождение критических точек, в которых возможен перегиб функции, достаточное условие наличия перегиба в окрестности критической точки;

–алгоритм нахождения наибольших и наименьших значений непрерывных функций в заданном интервале.

Студент должен уметь:

–проверять непрерывность, четность-нечетность и периодичность функции по ее аналитическому выражению (формуле);

–находить интервалы знакопостоянства функции и знаки функции в этих интервалах;

–выявлять интервалы возрастания-убывания функции с помощью первой производной и метода пробных точек;

–определять интервалы выпуклости вверх или вниз с помощью второй производной функции;

–находить точно или приближенно нули функции, критические точки первого или второго рода;

–определять возможные экстремумы функции в критических точках первого рода (точках стационарности) и перегибы функции в критических точках второго рода;

–находить наибольшее и наименьшее значения функции в заданном интервале;

–определять вертикальные, наклонные и горизонтальные асимптоты кривых.

147

Тема 10: Полное исследование функции и построение графика

10.1. Исходные положения

Полным исследованием будем называть исследование поведения функции в области ее естественного существования. Такое исследование целесообразно разбивать на два этапа:

–определение существенных свойств функции без использования производных (первый этап);

–то же с использованием производных функции (второй

этап); По результатам первого этапа строится предварительный эс-

киз графика функции, на котором в графической форме отражаются изученные на первом этапе свойства функции и прогнозируемые (предполагаемые) особенности ее поведения.

После этого выполняют второй этап исследования функции с использованием производных и затем строят окончательный график функции.

10.2. Общая схема полного исследования функции и построение графика в области существования

Пусть функция задана своим аналитическим выражением в явной форме y f x .

1. Исследование функции без использования производных. 1.1. Находим область существования функции X D f .

Замечание. У большинства функций, с которыми предстоит работать инженерам, областью существования является интервал (конечный, бесконечный или полубесконечный) или объединение конечного числа непересекающихся интервалов.

К области существования будем относить все значения аргумента, при которых функция непрерывна. Следовательно, в область существования элементарной функции не входят:

–значения аргумента, приводящие к делению на ноль, где функция терпит разрыв, в частности, отдельные значения аргумента для тангенса и котангенса;

–значения аргумента, при которых под корнем четной степени подкоренное выражение становится отрицательным;

–значения аргумента, при которых под знаком логарифма выражение отрицательно или равно нулю;

148

– значения аргумента, при которых под знаком арксинуса или арккосинуса выражение превосходит по модулю единицу.

После исключения указанных значений аргумента область существования представляют в виде объединения интервалов непрерывности, в которых значения функции являются действительными числами. Интервалы непрерывности разделяются точ-

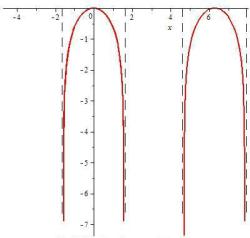
ками разрыва или интервалами разрыва. Например, область су-

ществования функции y lncosx имеет области разрыва, в кото-

Рис. 10.1. График функции y = ln cos x

1.2.Определяем вертикальные асимптоты на концах интервалов непрерывности и исследуем асимптотическое поведение функции на основе односторонних пределов в окрестности каждого из концов интервалов непрерывности.

1.3.Находим наклонные и горизонтальные асимптоты. При их наличии исследуем асимптотическое поведение функции.

Замечание. Для дробно-рациональных функций, представляющих собой отношение многочленов, левая и правая асимптоты совпадают (если хотя бы одна из них существует).

После определения уравнений асимптот исследуют асимпто-

149

lim f x kx b 0, то график функции расположен над пра-

x

вой асимптотой, если lim f x kx b 0, то под правой асим-

x

птотой. Для определения поведения функции относительно левой асимптоты аналогично рассматривается предел

lim f x kx b .

x

Пример. Найти асимптоты и исследовать асимптотическое

вертикальная асимптота x 0.

Левой асимптоты быть не может, так как функция не опреде-

Таким образом, имеет место наклонная асимптота y 1 x, 2

проходящая через начало координат.

Исследуем асимптотическое поведение функции около наклонной асимптоты при x :

значит, функция расположена выше асимптоты.

Для проверки асимптотического поведения функции можно использовать способ пробных точек. Для этого в случае вертикальной асимптоты выбирают значения аргумента, приближающиеся к точке разрыва и определяют знак и числовое значение функции. По этим данным судят о правильности вычисления одностороннего предела. Для рассмотренного примера в окрестно-

150