Моделирование электротехнических систем и систем автоматики

ном участке приращения аргумента. Как и прежде, вычисленное значение элементарной площади сохраняется в переменной S, значение которой увеличивается на каждом цикле приращения аргумента.

Рис. 23. Алгоритм интегрирования функции методом «трапеций»

51

Во всем остальном этот алгоритм аналогичен алгоритму предыдущего метода, в том числе и методу оценки точности полученного решения.

6.5. Принципы численного определения корней дифференциального уравнения

Корнем дифференциального уравнения называют такую функцию, дифференциал которой равен исходному уравнению. Решение дифференциального уравнения точным аналитическим методом не всегда возможно, а иногда бывает достаточно сложным. Это обстоятельство вызвало необходимость разработки приближенных методов решения дифференциального уравнения. Актуальность использования приближенных методов решения дифференциальных уравнений возросла с развитием вычислительной техники.

Для приближенного численного решения дифференциального уравнения существует несколько методов. Рассмотрим некоторые из них.

6.5.1. Принцип приближенного определения корней дифференциального уравнения методом Тейлора

Этот метод пригоден для решения любых дифференциальных уравнений. Суть этого метода состоит в том, что общее решение исходного уравнения представляет собой многочлен следующего вида:

Если известно х0 как начальное значение аргумента искомого решения, то его последующие значения в поиске решения находятся по формуле

где h – шаг дискретного приращения аргумента.

52

С учетом уравнения (32) общее решение дифференциального уравнения по методу Тейлора можно представить как

Чем больше значений ряда Тейлора будет присутствовать в выражении (33), тем точнее будет результат решения дифференциального уравнения. Однако решение дифференциальных уравнений этим методом сопряжено с трудностью определения производных, и особенно производных высших порядков. Поэтому этот метод мало применим для численного определения корней дифференциального уравнения.

6.5.2. Принцип приближенного определения корней дифференциального уравнения методом Эйлера

Принцип приближенного определения корней дифференциального уравнения методом Эйлера рассмотрим на графике некоторой функции, представленном на рис. 24.

Рис. 24. Схема графического дифференцирования по методу Эйлера

53

Начальное значение функции y = f(x) в точке x0, y0 заранее известно как начальное условие. Если провести через эту точку касательную к функции y = f(x), то все точки, лежащие на ней, будут производными этой функции. Поэтому производная в точке приращения аргумента (x0 + h)

где y′ − производная в точке (x0 + h).

Однако в точке (x0, y0) производная функции равна ее на-

Точки y1 и y2 являются производными функции y = f(x) с отклонениями ε1 и ε2 от истинного значения результата. Причем с увеличением аргумента это отклонение увеличивается, так как ε1 < ε2. Для уменьшения величины этой ошибки Эйлер усовершенствовал этот метод.

6.5.3. Принцип приближенного определения корней дифференциального уравнения усовершенствованным методом Эйлера

Графическая интерпретация усовершенствованного метода Эйлера представлена на рис. 25.

По этому методу Эйлер предложил угол между двумя смежными направлениями производных (например, L1 и L2) делить пополам, и в этом направлении проводить луч L3, который затем параллельно перенести в начальную точку (x0, y0) и продлить его до пересечения с ординатой x0 + h. Точку этого пересечения принять за искомый результат y2 на интервале очередного приращения аргумента. Величина отклонения ε2 этого результата намного

54

Рис. 25. Схема графического дифференцирования по усовершенствованному методу Эйлера

меньше первоначальной ошибки ε1. Для дальнейшего повышения точности определения корней дифференциального уравнения Эйлер модифицировал и этот метод.

6.5.4. Принцип приближенного определения корней дифференциального уравнения модифицированным методом Эйлера

Графическая интерпретация модифицированного метода Эйлера представлена на рис. 26.

Суть модифицированного метода Эйлера состоит в том, что в этом случае диапазон приращения аргумента на очередном шаге делится пополам и производная L2 вычисляется уже в точке А, находящейся на пересечении ординаты (x0 + h)/2 с лучом производной L1. После этого из точки (x0, y0) параллельно лучу L2 проводится луч L3 до пересечения с ординатой (x0 + h). Точка этого пересечения принимается за искомый результат y2 на интервале очередного приращения аргумента. Величина ошибки ε2 при этом минимальна.

55

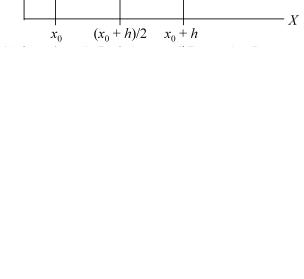
Рис. 26. Схема графического дифференцирования по модифицированному методу Эйлера

Этот метод Эйлера был успешно реализован Рунге и Куттом в алгоритме, названном их именами. В основу этого метода положен изложенный выше модифицированный метод Эйлера приближенного определения корней дифференциального уравнения.

6.5.5. Принцип и алгоритм численного определения корней дифференциального уравнения по методу Рунге–Кутта

Рунге и Кутт представили модифицированный метод Эйлера системой следующих уравнений:

56

В этой системе уравнение (38) описывает направление луча L1 из точки начального отсчета. Соответственно уравнение (39) это луч L2, проведенный из точки (x0 + h), а уравнение (40) это перенесенное а точку А направление луча L2. И, наконец, уравнение (41) это направление L3, проведенное из точки начального отсчета.

Алгоритм вычисления корней дифференциального уравнения по методу Рунге–Кутта представлен на рис. 27. После запуска этого алгоритма происходит ввод следующих исходных данных:

X0 − начальное значение аргумента;

Y0 − начальное значение результата; Xk − конечное значение аргумента; Кp − кратность вывода результата;

N − порядок дифференциального уравнения.

После ввода исходных данных параметрам X и Y присваиваются начальные значения, затем вводится параметр Zi, в котором сохраняется значение корня, полученного на предыдущей итерации. Первоначально Zi = Y0. Одновременно параметру К присваивается нулевое значение. С помощью этого параметра регулируется кратность вывода результата. После этих присвоений алгоритм обращается к подпрограмме «RGK», структура которой показана на рис. 28.

После выхода из подпрограммы «RGK» к параметру К добавляется единица, и его значение сравнивается с параметром Кр В случае равенства К и Кр производится вывод результата (X и Y), после чего параметр обнуляется К. Если условие К= Кр

57

не выполняется, то алгоритм, прежде чем выйти на очередную итерацию, проверяет другое условие, по которому параметр X не должен превышать параметр Xk, в противном случае приращение аргумента достигнет своего конечного значения и алгоритм должен остановиться.

Рис. 27. Алгоритм Рунге–Кутта вычисления корней дифференциального уравнения

58

Рис. 28. Структура подпрограммы «RGK» алгоритма Рунге–Кутта

Алгоритм работы подпрограммы «RGK», представленный на рис. 26, начинается с обращения к другой подпрограмме «ППЧ», в которой вычисляются правые части системы дифференциальных уравнений. Числовое значение правых частей уравнений используется при вычислении соответствующих коэффициентов по следующим формулам:

59

Расчет этих коэффициентов для системы уравнений производится в цикле, число повторений которого равно порядку N этой системы. В каждом цикле по формуле yi = zi + fk1, i/2 рассчитывается промежуточное значение параметра yi, значение которого уточняется в каждом из этих циклов.

Подпрограмма правых частей «ППЧ» представляет собой последовательность присвоений переменной совокупности алгебраических вычислений, соответствующих правым частям

Этот процесс повторяется четыре раза при каждом вычислении коэффициента fkj.

Вычисление корней системы дифференциальных уравнений методом Рунге–Кутта обеспечивает точность вычисления пропорциональной пятой степени шага интегрирования, т.е.

ε= h5.

Кнедостатку метода Рунге–Кутта нужно отнести невозможность использовать его для решения уравнений высших порядков (два и более). Поэтому в случае наличия таких уравне-

60