Теплофизические явления в полимерных материалах при интенсивном и кр

Объяснение этих фактов можно найти в так называемой аналогии свойств. Например, известна диффузионная аналогия [91], существо которой состоит в том, что уравнения стационарной теплопроводности и стационарной диффузии совпадают и отличаются только обозначениями. В то же время явление диффузии более наглядно, так как его можно рассматривать, наблюдая за поведением отдельной частицы.

В работе [91] отмечается идентичность математической постановки задач теплопроводности и электрофизических свойств (диэлектрической восприимчивости, электропроводности и др.) композиционных материалов с высокоасимметричными (иглообразными) включениями. В табл. 3.1 приведено соответствие терминов, употребляемых в задачах электро- и теплопроводности.

Таблица 3 . 1

Соответствие характеристик теплопроводности и электропроводности

Г.А. Гринберг [92] отмечает формальное совпадение дифференциальных уравнений скалярных и векторных полей для ста-

51

ционарных потоков тепла, электрического тока, электрической

имагнитной индукций. На этом основании Оделевский [3, 93] вводит понятие обобщенной проводимости, подразумевая под этим электропроводность, теплопроводность, диэлектрическую

имагнитную проницаемость. Оделевский отмечает, что для решения конкретной задачи можно использовать методы любой из этих областей.

И. Пригожин [94] упоминает обобщенные потоки (скорости, токи, световые потоки) и обобщенные силы без расшифровки этих понятий.

В.К. Семенченко [95] расширяет область свойств, для которых наблюдается аналогия, и вводит понятия обобщенных сил Х

иобобщенных координат х (табл. 3.2). К обобщенным силам он относит механические характеристики (давление для изотропных тел – газов или жидкостей, напряжение для анизотропного тела);

электрические и магнитные характеристики (напряженности E и

Hr соответственно для электрического и магнитного полей); термодинамическую характеристику (температуру); характеристику поверхностных явлений (поверхностное натяжение σ); характеристику многофазных систем (химический потенциал µ). К обобщенным координатам относит соответственно объем, деформацию, электрическую и магнитную индукции, энтропию, площадь поверхности, число частиц в системе. При таком подходе работа выражается произведением обобщенной силы и изменения обобщенной координаты:

dA = X dx.

В свете приведенной аналогии свойств рассмотрим явление диффузии, как наиболее наглядное.

Уравнение диффузии концентрации частиц для нереагирующего вещества записывается через плотность источников частиц и диффузионный поток, пропорциональный концентрации.

52

Уравнение зависимости концентрации реагирующего вещества из двух компонентов n(r,t) от времени имеет вид

частиц; s(r,t) – скорость реакции; j(r,t) – диффузионный поток, пропорциональный градиенту концентрации,

r r r uur r j(r,t) = −D(r) n(r,t);

D(r) – коэффициент диффузии.

изменения концентрации в элементарном объеме; в правой rr ur

части первое слагаемое (−u j(r,t)) – диффузионный поток сквозь поверхность элементарного объема; второе слагаемое (−s(rur,t) n(rur,t)) – уменьшение концентрации за счет реакции;

третье слагаемое (S(rur,t)) – плотность источников частиц внутри элементарного объема (рис. 3.1).

54

dz

S

s

dy

dx

Рис. 3.1. Изменение концентрации частиц в элементарном объеме: – диффузионный поток

сквозь поверхность, S – плотность источника внутри объема, s – частицы, реагирующие со скоростью s

где Db и sb – константы, характеризующие параметры «фоновой

среды».

Решение полученного уравнения после преобразования Фурье по времени примет вид

ur

где ω – частота; r' – фиксированная координата; δ – символ Кро- ur

некера; nb (r,ω) – концентрация, создаваемая в фоновой среде ис-

ur

точниками с плотностью S(r,t) .

rr

Вуравнении (3.2) Gb (r − r' ,ω) – функция Грина, имеющая

физический смысл пропагатора частицы в фоновой среде:

r

С учетом обращения в 0 интеграла по объему от G в статическом пределе (ω= 0) имеем:

56

Или, обозначая через Ф объемную долю компонента 1 с параметрами D1, s1, получаем:

57

Выражение (3.6) является общим для нахождения эффективных характеристик двухкомпонентных смесей.

Далее расчет распадается на две части.

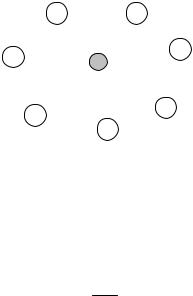
Если включений мало, фоном для выделенной частицы включения является матрица (рис. 3.2).

Рис. 3.2. Несимметричное приближение Максвелла–Гарнета: светлые кружки – частицы матрицы, темный кружок – выделенная частица включения

Тогда используем несимметричное приближение: DМ = Db , известное как приближение Максвелла–Гарнета [98]. В этом при-

ближении при s1 = s2 = 0 и gd = 3D1 b из (3.6) следует выражение

58

метр включения.

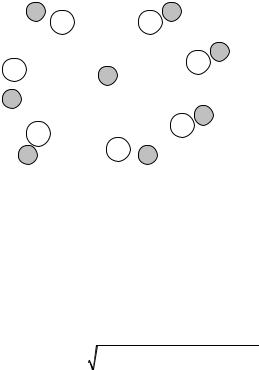
Если концентрации частиц включений и матрицы примерно равны, фоном для выделенной частицы включения является сама гетерогенная среда (рис. 3.3).

Рис. 3.3. Симметричное приближение Бруггемана: светлые кружки – частицы матрицы, темные кружки – частицы включения

В этом случае используем приближение самосогласованного поля: Db = Def , при котором фазы рассматриваются симметрич-

ным образом (в литературе оно называется приближением Бруггемана [98]). В этом приближении из (3.6) получим: