
Методы вычислительной математики
..pdf
|
|
Таблица 2.2 |
Результаты выполнения итерационной процедуры метода Якоби |
||
|
|
|
s |
x1(s ) |
x2(s ) |
0 |
0,0 |
0,0 |
1 |
1,25 |
1,8 |
2 |
0,35 |
1,05 |
3 |
0,725 |
1,59 |
4 |
0,255 |
1,365 |
5 |
0,5675 |
1,527 |
6 |
0,4865 |
1,4595 |
7 |
0,5203 |
1,5081 |
8 |
0,4959 |
1,4879 |
9 |
0,5061 |
1,5024 |
10 |
0,4988 |
1,4964 |
11 |
0,5018 |
1,5007 |
12 |
0,4996 |
1,4989 |
13 |
0,5005 |
1,5002 |
Матрица |
коэффициентов |
А может быть представлена в виде суммы |
||
A = A1 + D + A2 |
, где |
[A1 ]i j |
= ai j , |
i > j – нижняя треугольная матрица с нулевой |
диагональю; [A2 ]i j = ai j , |
i < j |
– верхняя треугольная матрица с нулевой диа- |
||
гональю; [D]i j |
= ai j , |
i = j – диагональная матрица. Систему уравнений Ax = f |
||
можно представить в виде
Ax = (A1 + D + A2 )x = f ,
Dx = f − (A1 + A2 )x,
и формула метода Якоби будет выглядеть следующим образом:
Dx(s+1) = f − (A1 + A2 )x(s).
Учитывая, что A1 + A2 = A − D , последнее выражение можно также представить в форме
|
|
D(x(s+1) − x(s) ) + Ax(s) = f . |
(2.14) |
|||
2.4.2. Метод Зейделя1 |
|
|
|
|
||
Для метода Зейделя выражение (2.13) преобразуется к виду |
|
|||||
(s+1) |
|
i−1 |
m |
|
|
|
|
(s+1) |
(s) |
aii , aii ≠ 0, i =1,m , |
(2.15) |
||
xi |
= |
fi − ∑ai j x j |
− ∑ai j x j |
|
||
|
|
j=1 |
j=i+1 |
|
|
|
1 Зейдель Филипп Людвиг [24.10.1821 – 13.8.1896] – немецкий астроном и математик. С 1851 стал членом Баварской академии наук; с 1854 – членом Геттингенской академии наук.
51
где s – номер итерации. В отличие от метода Якоби, теперь для вычисления очередной неизвестной xi(s+1) на s + 1 итерации используются найденные на той же итерации значения всех величин x(js+1), j =1,i −1. Как и ранее, вычислительный процесс заканчивается, когда выполняется условие
max x(js+1) − x(js) < ε,
1≤ j≤m
где ε > 0 – заданная погрешность вычисления результата.
|
x2 |
|
2 |
4x1 + 2 x2 = 5 |
|
|
|
|
1 |
|
|
3x1 + 5 x2 = 9 |
|||
|
|
|||||
|
|
|
||||
|
|
|
|
|
|
|
0 |
|
|
|
|
x1 |
|
|
|
2 |
|
|
|
|
1 |
|
|
3 |
|
|
|
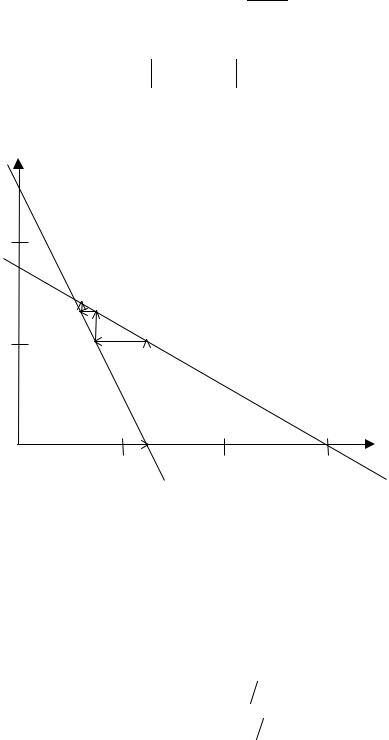
Рис. 2.4. Схема выполнения метода Зейделя |
||||||
Пример 2.4. Решить систему линейных алгебраических уравнений |
||||||
4x1 + 2x2 |
= 5, |
|
|
|
||
|
3x1 |
+ 5x2 |
= 9 |
|
|
|
|
|
|
|
|||
методом Зейделя. |
|
|
|
|
|
|
Точное решение этой системы: x1 = 0,5, x2 = 1,5.
Уравнения системы записываются в виде итерационной схемы Зейделя: |
||
x(s+1) |
= (5 |
− 2x(s) ) 4, |
1 |
|
2 |
|
= (9 |
− 3x(s+1) ) 5. |
x(s+1) |
||
2 |
|
1 |
Это означает, что для нахождения x2 на s + 1 итерации используется значение x1, вычисленное ранее на этойже итерации. В качестве начального приближения принимаются x(0) = 0 , y(0) = 0. Результаты расчетов сведены в табл. 2.3. Нарис. 2.4 показан ход выполнения итерационной процедуры Зейделя.
52
Таблица 2.3 Результаты выполнения итерационной процедуры метода Зейделя
|
|
|
N |
x1(n) |
x2(n) |
0 |
|
0 |
1 |
1,25 |
|
|
|
1,05 |
2 |
0,725 |
|
|
|
1,365 |
3 |
0,5675 |
|
|
|
1,4595 |
4 |
0,5203 |
|
|
|
1,4879 |
5 |
0,5061 |
|
|
|
1,4964 |
6 |
0,5018 |
|
|
|
1,4989 |
7 |
0,5005 |
|
|
|
1,4997 |
Как и в предыдущем случае, матрица коэффициентов А представляется в виде суммы A = A1 + D + A2 с теми же обозначениями. Итерационную форму-
лу метода Зейделя можно представить в форме
(A1 + D)x(s+1) = f − A2 x(s) .
Учитывая, как и ранее, что A2 = A − A1 − D , последнее выражение можно записать в виде итерационной схемы
(A + D)(x(s+1) − x(s) )+ Ax(s ) = f . |
(2.16) |
1 |
|
2.4.3. Сходимость итерационных методов
Сравнивая формулы (2.14) метода Якоби и (2.16) метода Зейделя, можно заметить, что если последовательность решений сходится, то есть в некотором смысле (x(s+1) − x(s) )→ 0, s → ∞ , то она сходится к решению исходной задачи,
поскольку в этом случае имеет место Ax(s) = f , s → ∞.
Пример 2.5. Решить систему линейных алгебраических уравнений:
4x1 + 2x2 = 5, |
|||||
|
|
|
|
|
|
|
|
+ 5x |
|
= −2,5. |
|
− 20x |
2 |
||||
|
1 |
|
|
|
|
Точные значения неизвестных |
величин этой системы известны: |
||||
x1 = 0,5, x2 =1,5. Для нахождения решения используется метод Зейделя. Как и ранее, уравнения системы записываются в виде итерационной схемы:
53
x(s+1) |
= (5 |
− 2x(s) ) |
4, |
|
|
1 |
|
2 |
|
|
|
= (− 2,5 + 20x(s+1) ) 5. |
||
x(s+1) |
||||
|
2 |
|
|
1 |
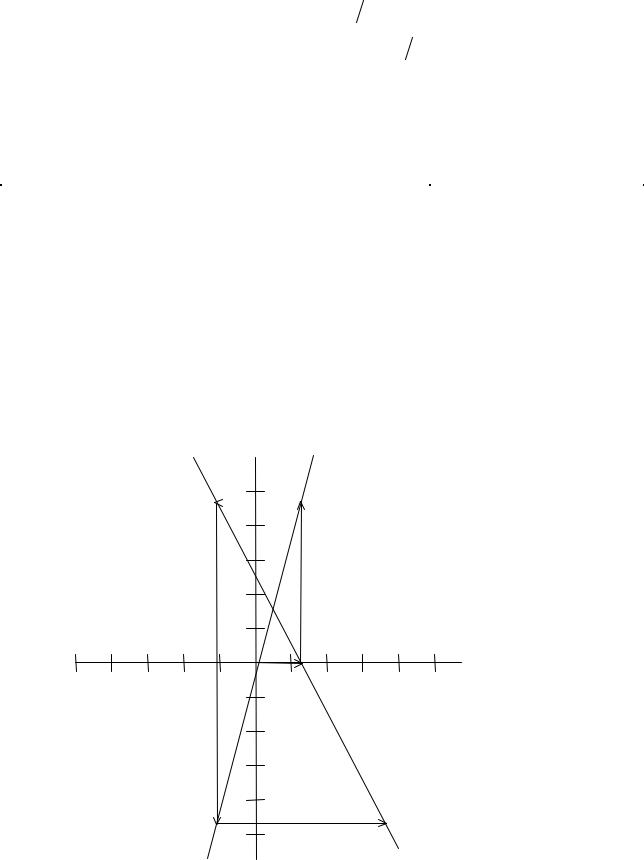
Результаты вычислений представлены в табл. 2.4. На рис. 2.5 отражен ход поиска решения системы линейных алгебраических уравнений методом Зейделя.
|
|
|
|
|
|
|
Таблица 2.4 |
Результаты выполнения итерационной процедуры метода Зейделя |
|||||||
n |
|
|
|
x1(n) |
|
|
x2(n) |
0 |
|
|
|
|
|
|
0,0 |
1 |
|
|
|
|
|
1,25 |
|
|
|
|
|
|
|
|
4,5 |
2 |
|
|
|
|
|
–1,0 |
|
|
|
|
|
|
|
|
–4,5 |
3 |
|
|
|
|
|
3,5 |
|
|
|
|
|
|
|
|
13,5 |
4 |
|
|
|
|
|
–5,5 |
|
|
|
|
|
|
|
|
–22,5 |
5 |
|
|
|
|
|
12,5 |
|
|
|
|
|
… |
|
|
49,5 |
|
|
5 |
x2 |
–20x1 + 5x2 = –2,5 |
|||
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
1 |
2 |
3 |
4 |
5 |
|
|
|
|||||
–5 –4 –3 –2 –1 |
|
–1 |
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
–2 |
|
|
|
|
|
|
|
–3 |
|
|
4x1 + 2x2 = 5 |
|
|
|
|
–4 |
|
|
||
|
|
|
|
|
|
|
|
–5
Рис. 2.5. Отсутствие сходимости решения при использовании метода Зейделя
54

Расчеты показывают, что в рассматриваемом примере отсутствует сходимость последовательности результатов к точному решению. Это приводит к необходимости определения условий сходимости той или иной итерационной процедуры.
Итерационные методы решения систем линейных алгебраических уравнений можно записать в канонической форме с использованием итерационных параметров B(s+1) и τ(s+1) :
B(s+1) (x(s+1) − x(s) ) τ(s+1) + Ax(s) = f , s = 0,1, 2, ... . |
(2.17) |
В случае, если B(s+1) и τ(s+1) не зависят от номера итерации s, метод назы- |
|
вается стационарным. В частности, для метода Якоби B(s+1) = D, |
τ(s+1) =1; для |
метода Зейделя B(s+1) = A1 + D, τ(s+1) =1.
Если B(s+1) = E , метод называется явным; в противном случае – неявным. Примеры итерационных методов:
– явный стационарный метод простых итераций:
(x(s+1) − x(s) ) τ + Ax(s) = f ;
τ + Ax(s) = f ;
– неявный стационарный метод верхней релаксации:
(D + ωA1 )(x(s+1) − x(s) ) ω + Ax(s) = f , ω > 0 .
ω + Ax(s) = f , ω > 0 .
В пространстве m-мерных векторов Rm со скалярным произведением
m
(u,v)= ∑uivi
i=1
и нормой
m

 w
w
 =
=  (w, w) = ∑wi2
(w, w) = ∑wi2
i=1
определяется матричное неравенство: квадратная матрица C > 0 тогда и только тогда, когда
(Cx, x) > 0 x H , x ≠ 0 .
Иначе это определение может быть записано следующим образом [9]:δ > 0, (Cx, x) ≥ δ
 x
x
 2 , x ≠ 0.
2 , x ≠ 0.
55

Эта оценка позволяет утверждать, что существует обратная матрица C −1 , так как в случае положительной определенности матрицы все ее главные (угловые) миноры положительны (критерий Cильвестра1, [9]).
Для установления условий сходимости формулой z(s) = x(s) − x определяется погрешность метода, и тогда из формулы (2.17) для стационарного итерационного метода можно получить
B(z(s+1) + x − z(s) − x) τ + Az(s) + Ax = f , |
|
B (z( s +1) − z( s) ) τ + Az( s ) = f , s = 0, 1, ... . |
(2.18) |
Теорема 2.4. Пусть А – симметричная положительно определенная матрица, A > 0. Итерационные параметры удовлетворяют соотношению
B −τA 2 > 0, τ > 0 .
2 > 0, τ > 0 .
Тогда стационарный итерационный метод сходится.
Доказательство. Для доказательства теоремы следует показать, что по-
грешность метода z(s) →0 при любой начальной погрешности z(0) . Для
s→∞
этого строится числовая последовательность вида J (s) = (Az(s) , z(s) ). Из фор-
мулы (2.18) следует
z(s+1) = z(s ) − τB−1 Az(s) , Az(s+1) = Az(s ) − τAB−1 Az(s ) .
Теперь можно подсчитать
J (s+1) = (Az(s+1) , z(s+1) )= (Az(s) − τAB−1 Az(s) ,z(s) − τB−1 Az(s) )=
= (Az(s) , z(s) )− τ(AB−1 Az(s) ,z(s) )− τ(Az(s) ,B−1 Az(s) )+ τ2 (AB−1 Az(s) ,B−1 Az(s) ).
Вследствие симметрии матрицы А имеет место равенство
(AB−1 Az(s) , z(s) )= (Az(s) , B−1 Az(s) ).
Отсюда следует:
J (s+1) = (Az(s) , z(s) )− 2τ(Az(s) , B−1 Az(s) )+ τ2 (AB−1 Az(s) , B−1 Az(s) )=
= J (s) − (2τAz(s) − τ2 AB−1 Az(s) , B−1 Az(s) ) = J (s) − 2τ((B − τA 2)B−1 Az(s) , B−1 Az(s) ) =
2)B−1 Az(s) , B−1 Az(s) ) =
=J (s ) − 2τ((B − τA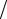 2)u(s) ,u(s) ),
2)u(s) ,u(s) ),
1Сильвестр Джеймс Джозеф [3.9.1814 – 15.3.1897] – английский математик. Окончил Кембриджский университет в 1837 году. С 1855 по 1870 годы являлся профессором Королевской академии в Вулидже; с 1876 по 1883 год – профессором университета Джона Хопкинса в г. Балтиморе; с 1883 года – профессором Оксфордского университета; с 1872 года – иностранным членом-корреспондентом Петербургской академии наук.
56

где u(s) = B−1 Az(s) . В силу условия теоремы [(B − τA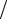 2)u(s) , u(s) ]> 0 u(s) , следует, что J (s+1) ≤ J (s ) , то есть построенная последовательность является монотонно убывающей и, кроме того, в силу J (s+1) = (Az(s+1), z(s+1) )> 0 ограничена снизу. Отсюда вытекает, что существует предел этой последовательности
2)u(s) , u(s) ]> 0 u(s) , следует, что J (s+1) ≤ J (s ) , то есть построенная последовательность является монотонно убывающей и, кроме того, в силу J (s+1) = (Az(s+1), z(s+1) )> 0 ограничена снизу. Отсюда вытекает, что существует предел этой последовательности
J = lim J (s) .
s→∞
Из положительной определенности (B − τA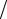 2)> 0 следует существование константы δ > 0 такой, что имеет место
2)> 0 следует существование константы δ > 0 такой, что имеет место
((B − τA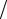 2)B−1 Az(s) , B−1 Az(s) )≥ δ
2)B−1 Az(s) , B−1 Az(s) )≥ δ
 B−1 Az(s)
B−1 Az(s) 
 2 .
2 .
Предыдущее выражение может быть переписано в форме неравенства:
J (s+1) = J (s) − 2τ((B − τA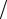 2)B−1 Az(s) , B−1 Az(s) )≤ J (s ) − 2τδ
2)B−1 Az(s) , B−1 Az(s) )≤ J (s ) − 2τδ
 B−1 Az(s)
B−1 Az(s) 
 2 .
2 .
При s → ∞ из последнего выражения следует
J ≤ J − 2τδlim B−1 Az(s) 2 .
s→∞
Очевидно, что неравенство lim B−1 Az(s) 2 ≤ 0 может выполняться лишь при
s→∞
условии, что lim |
|
|
|
B−1 Az(s) |
|
|
|
= lim |
|
|
|
u(s) |
|
|
|
= 0 . С другой стороны, z(s) = A−1Bu(s) , при- |
|
|
|
|
|
|
|
|
|||||||||
s→∞ |
|
|
|
|
|
|
|
s→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
чем A−1 существует в силу положительной определенности матрицы А, как это определено условием теоремы. Норма погрешности оценивается выражением

 z(s)
z(s) 
 =
= 
 A−1Bu(s)
A−1Bu(s) 
 ≤
≤ 
 A−1B
A−1B


 u(s)
u(s) 

Теперь становится очевидным, что вследствие
z (s) →0. Что и требовалось доказать.
s→∞
.
lim u(s) = 0 имеет место
s→∞
Следствие 1. Пусть А – симметричная положительно определенная матрица. Тогда метод верхней релаксации
(D + ωA1 )(x(s+1) − x(s) )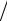 ω + Ax(s) = f , ω > 0
ω + Ax(s) = f , ω > 0
сходится при 0 < ω < 2. В частности, метод Зейделя (ω = 1) сходится.
Доказательство. В рассматриваемом случае B = D + ωA1, τ = ω,
(Ax, x) = ((A1 + D + A2 )x, x) = (A1 x, x)+ (Dx, x)+ (A2 x, x) = (Dx, x)+ 2(A1 x, x).
Последнее соотношение справедливо в силу симметрии матрицы А:
m |
m |
(A1x, x)= ∑aij1 x j xi = ∑a2ji xi x j = (A2 x, x). |
|
i, j=1 |
i, j=1 |
57

Условие сходимости итерационного метода B −0,5τA > 0, τ > 0 теоремы 2.4
принимает вид
((B − ωA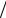 2)x, x) = (Bx, x) − ω(Ax, x)
2)x, x) = (Bx, x) − ω(Ax, x)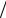 2 = (Dx, x) + ω(A1x, x)− ω[(Dx, x)+ 2(A1x, x)]
2 = (Dx, x) + ω(A1x, x)− ω[(Dx, x)+ 2(A1x, x)]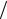 2 = = (Dx, x)+ω(A1x, x)−ω(Dx, x)
2 = = (Dx, x)+ω(A1x, x)−ω(Dx, x)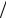 2 −ω(A1x, x) = (1−ω
2 −ω(A1x, x) = (1−ω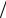 2)(Dx, x) > 0.
2)(Dx, x) > 0.
Очевидно, что последнее неравенство выполняется при условии
1−ω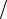 2 > 0, 0 < ω< 2 .
2 > 0, 0 < ω< 2 .
Следствие 2. Пусть А – симметричная положительно определенная матрица с диагональным преобладанием, то есть имеет место
aii > ∑ ai j , i, j =1,m .
i≠ j
Тогда метод Якоби сходится.
Доказательство. Поскольку в рассматриваемом случае B = D, условие сходимости принимает вид неравенства 2D > A . Из неравенств
(xi − x j )2 = xi2 − 2xi x j + x2j ≥ 0 , xi x j ≤ (xi2 + x2j ) 2
2
получается:
m |
|
1 |
m |
1 |
m |
|
1 |
m |
1 |
m |
|||||||||||||||||
(Ax, x) = ∑aij xi x j |
≤ |
∑ |
|
aij |
|
xi2 + |
∑ |
|
aij |
|
x2j |
= |
∑ |
|
aij |
|
xi2 + |
∑ |
|
a ji |
|
xi2 . |
|||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
i, j=1 |
|
2 i, j=1 |
|
|
|
|
2 i, j=1 |
|
|
|
|
|
2 i, j=1 |
|
|
|
|
2 i, j=1 |
|
|
|
|
|||||
В силу симметричности и положительной определенности А следует:
m |
|
|
m |
|
|
|
|
(Ax, x)≤ ∑ |
aij |
2 |
|
∑ |
aij |
|
2 |
xi |
= ∑ |
+ aii xi . |
|||||
i, j=1 |
|
|
i=1 |
j≠i |
|
|
|
Использование предположения следствия приводит к выражению
2aii > ∑ ai j + aii , i =1,m . i≠ j
Из двух последних неравенств получается
m
(Ax, x)< 2∑aii xi2 = 2(Dx, x).
i=1
Что и требовалось доказать.
2.4.4. Итерационный метод с чебышёвским набором параметров
Рассматривается система линейных алгебраических уравнений Ax = f с симметричной положительно определенной матрицей А. Решение разыскивается с помощью явного нестационарного метода Ричардсона,
58

(x(s+1) − x(s) ) τ(s+1) + Ax(s) = f , s = 0,1, 2, …
τ(s+1) + Ax(s) = f , s = 0,1, 2, …
Следует так определить набор итерационных параметров τ(1) , τ(2) , …, τ(n) , чтобы норма 
 x(n) − x
x(n) − x
 была минимальной для заданного числа итераций n.
была минимальной для заданного числа итераций n.
Теорема 2.5. Пусть А – симметричная положительно определенная матрица, λmin > 0, λmax > 0 – ее наименьшее и наибольшее собственные значения; за-
дано число итераций n. Среди всех наборов τ(s) , |
s = |
1,n |
, наименьшую погреш- |
|||||||||||||||||||||||||||
ность |
|
|
|
x(n) − x |
|
|
|
|
|
|
|
имеет набор, для которого |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ(s) = τ(0) (1 + ρ0t(s) ), s = |
|
|
, |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,n |
|
|
|
|||||||||||||
τ(0) = 2 (λmin + λmax ); |
|
|
|
ρ0 = (1 − ξ) (1 + ξ); |
ξ = λmin |
λmax ; |
t(s) |
= cos((2s −1)π 2n). |
||||||||||||||||||||||
Оценка погрешности в этом случае имеет вид |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
x(n) − x |
|
|
|
≤ q(n) |
|
|
|
x(0) − x |
|
|
|
, q(s) = 2ρn |
(1 + ρ2n ), |
ρ = (1 − |
ξ) (1 + ξ). |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|||
Доказательство. Вводится погрешность решения |
z(s) |
= x(s) − x , относи- |
||||||||||||||||||||||||||||
тельно которой записывается система уравнений схемы Ричардсона: |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(z(s+1) − z(s) ) τ(s+1) + Az(s) = 0, s = |
|
. |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0,n −1 |
|
||||||||||||||||
Отсюда получается зависимость |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z(s+1) = z(s) − τ(s+1) Az(s) = (E − τ(s+1) A)z(s) . |
|
|||||||||||||||
В частности, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z(1) = (E − τ(1) A)z(0) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z(2) |
|
|
|
= (E − τ(2) A)z(1) = (E − τ(2) A)(E − τ(1) A)z(0) , |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. . . |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z(n) = ∏n (E − τ(s) A) z(0) . |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s=1 |
|
|
|
|
|
|
|
|
|
Вводится обозначение |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
T (n) = (E − τ(n) A)(E − τ(n−1) A) … (E − τ(1) A)= ∏n |
(E − τ(s) A). |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s=1 |
|
|
|
|
По построению T (n) – симметричная матрица. Погрешность на n-й итерации можно представить выражением
z(n) =T (n) z(0) , 
 z(n)
z(n) 
 =
= 
 T (n) z(0)
T (n) z(0) 
 .
.
59

Для симметричной положительно определенной матрицы в качестве нормы может быть выбран спектральный радиус ν = λmax (T (n) ) . Действительно, для собственного вектора V, соответствующего собственному значению λmax ,
T (n)V = λmaxV ,

 T (n)V
T (n)V 
 =
= 
 λmaxV
λmaxV 
 = λmax
= λmax 

 V
V 
 = ν
= ν
 V
V 
 .
.
Сучетом свойств нормы получается
ν
 V
V 
 =
= 
 T (n)V
T (n)V 
 ≤
≤ 
 T (n)
T (n) 


 V
V 
 ,
,
ν ≤ 
 T (n)
T (n) 
 .
.
Предполагая, что V k , k =1,m , – ортонормированная построенная на основе собственных векторов матрицы T (n) ,
(V k , V j ) m VikVi j = δkj ,
= ∑
i=1
можно разложить вектор V по этому базису:
m
V = ∑ckV k .
k=1
(2.19)
система векторов,
Согласно определению нормы вектора
|
V |
|
2 |
|
m |
m |
|
m |
|
m |
|
|
|
|
|
|
|||||
|
|
|
= (V , V )= |
∑ckV k , ∑c jV j |
|
= ∑ |
∑ckVik |
|||
|
|
|
|
|||||||
|
|
|
|
k=1 |
j=1 |
|
i=1 |
k=1 |
||
m |
|
|
∑c jVi |
j |
= |
|
||
j=1 |
|
|
|
|
|
|
|
|
|
|
= ∑ |
ck c j |
∑(VikVi j |
) = ∑(ck c j δkj )= ∑ck2 . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
m |
|
m |
|
|
|
|
m |
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
k , j=1 |
i=1 |
|
|
k , j=1 |
|
|
k =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
В компонентной записи вектор T (n)V с использованием |
|
|
собственных чи- |
||||||||||||||||||||||||||||||||||
сел и векторов выглядит следующим образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
{T |
(n) |
m |
(n) |
m |
|
(n) |
m |
|
k |
= |
m |
|
m |
(n) k |
|
|
|
|
|
|
|
m |
k |
. |
|
||||||||||||
|
|
|
|
|
V}i = ∑Ti j Vj |
= ∑ Ti j |
∑ckVj |
∑ck |
∑Ti j |
Vj |
|
|
|
= ∑ck λkVi |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
j=1 |
|
j=1 |
|
|
k=1 |
|
|
|
|
k=1 |
|
j=1 |
|
|
|
|
|
|
|
|
|
k=1 |
|
|
|
||||||
|
Учитывая, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
T ( n)V |
|
|
|
2 = (T ( n )V ,T ( n )V )= m |
m |
c |
λ |
V k |
m |
c |
j |
λ V j |
= |
m |
c |
c |
λ |
λ |
j |
m V kV j |
= |
||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
∑ |
∑ k |
k |
i |
∑ |
j i |
|
|
∑ |
k |
|
|
|
j |
|
|
k |
|
∑ i i |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
i =1 |
k =1 |
|
|
|
j =1 |
|
|
|
|
|
k , j =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
m |
|
|
|
|
m |
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ∑ (ck cjλkλjδkj ) = ∑(ck2λ2k ) ≤ λmax2 |
∑ck2 = λmax2 |
|
|
|
V |
|
|
|
2 , |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
k , j=1 |
|
|
|
k=1 |
|
|
|
|
|
k=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
можно подсчитать норму оператора
60
