
Экономические задачи линейного программирования и их решение с испол
..pdfВячейку G17 введемформулу =СУММПРОИЗВ(C3:C15;G3:G15),
вячейку G18 введем формулу =СУММПРОИЗВ(D3:D15;G3:G15),
вячейкуG19 введемформулу=СУММПРОИЗВ(E3:E15;G3:G15).
Вячейку G16 запишем формулу для целевой функции
=G19/H19.
Вячейку G20 введем формулу суммы всех деталей
=СУММ(G17:G19).
Для поиска оптимального набора значений переменных, который соответствует максимальному значению целевой функции, следует воспользоваться надстройкой Поиск решения. Заполним диалоговое окно надстройки (рис. 3.26):
1. В поле Оптимизировать целевую ячейку введем адрес целевой функцииG16.
2. Ниже выберем параметр Максимум.
3. В поле Изменяя ячейки переменных введем диапазон ячеек с искомыми переменными G3:G15.
4. Установим флажок Сделать переменные без ограничений неотрицательными и выберем параметр Поиск решения линейных задач симплекс-методом.
5. Щелчком по кнопке Добавить вызовем окно Добавление ограничения. В этом окне введем ссылки на ячейки ограничений, а также выберем оператор ограничений. Для решения данной задачи нам необходимы следующие ограничения:
– H3 ≤ 50 – ограничение на количество материала первого вида,
– H9 ≤ 60 – ограничение на количество материала второго вида,
– G17 ≥3·G16 – условиекомплектностизаготовокпервоговида,
– G18 ≥2·G16 – условиекомплектностизаготовоквтороговида,
– G19 ≥1·G16 – условиекомплектностизаготовоктретьеговида. 6. Нажав кнопку Найти решения, получим результаты решения.
Вокне Результаты поиска решения выберем отчет и сохра-
ним полученный результат как сценарий (кнопка Сохранить сце-
нарии) с именем Раскрой.
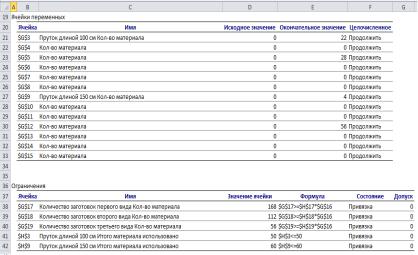
На рис. 3.27 приведен результат решения задачи по оптимальному раскрою материала.
141
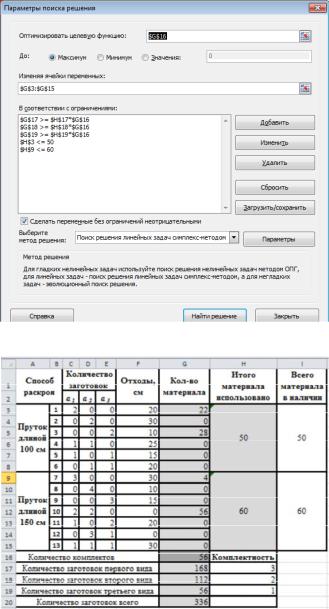
Рис. 3.26
Рис. 3.27
142
Анализ отчетов
Теперь необходимо проанализировать отчеты, которые получили при решении задачи.
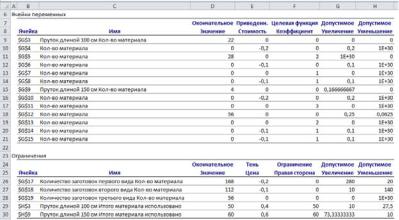
На рис. 3.28 представлен отчет о результатах. Оптимальное значение целевой функции:
zmax = 56 комплектов, zmax = 336 деталей.
Рис. 3.28
Значения основных переменных прямой задачи (количество продуктов, раскроенных различными способами):
х1 = 22, |
х6 |
= 0, |
х11 |
= 0, |
|
х2 |
= 0, |
х7 |
= 4, |
х12 |
= 0, |
х3 |
= 28, |
х8 |
= 0, |
х13 |
= 0. |
х4 |
= 0, |
х9 |
= 0, |
|
|
х5 |
= 0, |
х10 = 56, |
|
|
|
Количество использованных ресурсов (прутки) и произведенных заготовок:
Материал первого вида = 50. Материал второго вида = 60.
143
Заготовки первого вида = 168. Заготовки второго вида = 112. Заготовки третьего вида = 56.
Значения дополнительных переменных прямой задачи (допуск) – остатки ресурсов и количество заготовок, произведенных сверх комплекта:
Материал первого вида = 0. Материал второго вида = 0. Заготовки первого вида = 0. Заготовки второго вида = 0. Заготовки третьего вида = 0.
На рис. 3.29 представлен отчет об устойчивости.
Рис. 3.29
Проанализировав данные отчета об устойчивости, получим следующие значения:
Приведенная стоимость – это значения дополнительных переменных двойственной задачи; они соответствуют основным переменным прямой задачи и оценивают тот или иной вариант плана:
–х1 соответствует приведенная стоимость, равная 0;
–х2 соответствует приведенная стоимость, равная –0,2;
–х3 соответствует приведенная стоимость, равная 0;
144
–х4 соответствует приведенная стоимость, равная –0,1;
–х5 соответствует приведенная стоимость, равная 0;
–х6 соответствует приведенная стоимость, равная –0,1;
–х7 соответствует приведенная стоимость, равная 0;
–х8 соответствует приведенная стоимость, равная –0,2;
–х9 соответствует приведенная стоимость, равная 0;
–х10 соответствует приведенная стоимость, равная 0;
–х11 соответствует приведенная стоимость, равная 0;
–х12 соответствует приведенная стоимость, равная –0,1;
–х13 соответствует приведенная стоимость, равная –0,1. Соответствующие способы раскроя 1, 3, 7 и 10 (см. табл. 3.5)
использовать выгодно, они вошли в оптимальный план, так как приведенная стоимость равна 0. Способы раскроя 2, 8 – самые неудачные, так как приведенная стоимость максимальна по абсолютной величине.
Значения основных переменных двойственной задачи (теневая цена) – двойственная оценка единицы материала:
Материал первого вида = 0,4. Материал второго вида = 0,6.
Наиболее эффективен материал второго вида, так как двойственная оценка в этом случае макисмальна.
Диапазон устойчивости двойственных оценок ресурсов: 22,5 ≤ Материал первого вида ≤ 60.
50 ≤ Материал второго вида ≤ 133,3, т.е. изменение количества материала в данных пределах не повлия-
ет на значения двойственных оценок, а следовательно, и на эффективность дополнительной единицы соответствующего материала.
Анализ отчетов и выводы по анализу аналогичны представленым в подразд. 2.6 и 2.7.
3.6.Задача оптимального развития
иразмещения производства
Нередко возникают ситуации, когда мощность предприятия формируется за счет крупных, неделимых агрегатов и изменяется дискретно, принимая только вполне определенные значения, крат-
145
ные составляющим ее агрегатам. В этом случае функция, отражающая зависимость затрат от объема производства, будет представлять дискретный набор точек, соответствующих дискретно меняющимся значениям мощности. Таким образом, мы имеем задачу целочисленного программирования.
Такие же задачи возникают и тогда, когда для каждого пункта рассчитывается конечное число проектов строительства предприятий различной мощности и оптимальная мощность должна совпадать с мощностью одного из проектов.
Постановка задачи
Имеется т возможных пунктов производства какой-то продукции одного наименования и п пунктов потребления. В каждом пункте потребления известен перспективный спрос bj (j = 1, 2, …, n).
Задана матрица транспортных затрат на единицу продукции 
 tij
tij 
 m n
m n
(i = 1, 2, …, m; j = 1, 2, …, n). В каждом из возможных пунктов производства задано ki вариантов строительства предприятий, пронумерованных в порядке возрастания их мощности xi
(Ai1, Ai2 , ..., Aik ) . Каждому варианту соответствует значение функ-
ции φi(xi), характеризующей зависимость приведенных затрат на продукцию от объема производства в пункте i.
Требуется определить показатели хij – величины поставок i-го поставщика j-му потребителю с целью получения минимума суммарных затрат на производство и транспортировку продукции.
Моделирование
Математическая модель задачи примет следующий вид. Целевая функция
m |
m |
n |
z i xi tij xij min. |
||
i 1 |
i 1 |
j 1 |
146

Система ограничений:
m |
|
|
|
|
xij bj , |
i 1, 2, ..., n, |
|
||
i 1 |
|
|
|
|
n |
x , |
|
xi Ai1, Ai2 , Aik (i 1, 2, ..., m; k 1, 2, ..., ki ), |
|
xij i |
|
|||
j 1 |
0, |
|
|
|
|
xi 0, |
xij 0 (i 1, 2, ..., m; |
j 1, 2, ..., n), |
|
где Aik – мощность предприятия в i-м пункте по k-му проектному
варианту.
Это задача целочисленного программирования.
Одним из наиболее удачных (с практической точки зрения) способов решения задач развития и размещения в целочисленной постановке является предложенный В.Н. Гофманом метод «коэф-
фициентов интенсивности».
Суть этого метода состоит в следующем. Решается открытая транспортная задача с максимально возможными мощностями для
всех пунктов производства xi Aik i 1, 2, , m и ограничением
n
xij xi .
j1
Воптимальном решении могут оказаться поставщики (предприятия), связанные как с реальными потребителями, так и с фиктивными (строки таких предприятий в транспортной модели называются смешанными). Для всех смешанных строк вычисляется коэффициент интенсивности как отношение сумм поставок реальным потребителям к мощности:
n xij
ki |
j 1 |
. |
|
||
|
xi |
|
147
Очевидно, что коэффициент интенсивности для предприятия, связанного с реальными потребителями, равен 1, а с фиктивными – 0. Для смешанныхстроккоэффициентбольшенуля, номеньшеединицы.
Далее среди всех смешанных строк выбирается та, которой соответствует наименьший коэффициент. Она называется переходной. Для этой строки осуществляется переход на меньшую мощность, что ведет, естественно, к увеличению затрат на единицу продукции в этой строке и уменьшению ее конкурентоспособности, так что по тенденции она на последующих итерациях получит еще меньший, а может быть, и нулевой коэффициент интенсивности. Затем вновь рассматривается открытая модель транспортной задачи, вычисляются коэффициенты, выбирается очередная переходная строка и т.д. Процесс итерационный, в конечном счете все коэффициенты будут равны 0 или 1. Выбор в качестве переходной строки, обладающей наименьшим коэффициентом интенсивности, основан на гипотезе, что вероятность вхождения такого предприятия в оптимальный план крайне мала.
Пример решения задачи в Microsoft Excel
Постановка задачи
Имеется четыре пункта потребления однородного продукта (b1, b2, b3, b4). Спрос потребителей на конечный год планового периода известен и составляет соответственно 15, 5, 10, 10 т. К моменту начала расчетов в отрасли существует всего два предприятия а1 и а2, мощности которых составляют: а1 – 15 т, а2 – 15 т. Как видим, необходимо развитие отрасли, так как спрос на перспективу составит 40 т. Предприятия а1 и а2 могут расширяться за счет добавления новых технологических линий, каждая из которых обеспечивает увеличение мощности на 5 т. При этом возможно расширение на одну или две технологические линии, не более. Планируется строительство нового предприятия в пункте а3 мощностью 15 или 20 т.
Все варианты возможного функционирования предприятий на перспективу и их показатели приведены в табл. 3.7.
148

|
|
Таблица 3.7 |
|
|
|
|
|
Поставщики |
Варианты |
Приведенные |
|
мощности, т |
затраты, руб/т |
||
|
|||
а1 |
15 |
24 |
|
20 |
21 |
||
|
25 |
20 |
|
а2 |
15 |
23 |
|
20 |
20 |
||
|
25 |
19 |
|
а3 |
15 |
22 |
|
20 |
21 |
||
|
Потребители продукции и все предполагаемые поставщики связаны транспортной сетью. Затраты на перевозки представлены в табл. 3.8.
|
|
|
|
|
Таблица 3.8 |
|
|
|
|
|
|
|
|
|
|
Тарифы на перевозку, руб/т, |
||||
Поставщики |
|
|
для потребителей |
|
|
|
|
b1 |
|
b2 |
b3 |
|
b4 |
а1 |
7 |
|
3 |
2 |
|
3 |
а2 |
3 |
|
2 |
4 |
|
6 |
а3 |
1 |
|
4 |
5 |
|
4 |
Потребность, т |
15 |
|
5 |
10 |
|
10 |
Требуется определить оптимальный план развития отрасли (где строить и какой мощности) с целью получения минимума суммарных затрат на производство и транспортировку готовой продукции, а также установить оптимальные связи между производителями и потребителями.
Моделирование
Обозначим переменные величины:
–xij (i 1,3; j 1,4) – искомые переменные;
–х11 – количество ресурсов, перевозимых от поставщика а1
кпотребителю b1;
149
–х12 – количество ресурсов, перевозимых от поставщика а1
кпотребителю b2;
–х13 – количество ресурсов, перевозимых от поставщика а1
кпотребителю b3;
–х14 – количество ресурсов, перевозимых от поставщика а1
кпотребителю b4.
Аналогично для остальных поставщиков. Тогда целевая функция
z= 27x11 + 23x12 + 22x13 + 23x14 + 22x21 + 21x22 +
+23x23 + 25x24 + 22x31 + 25x32 + 26x33 + 25x34 → min.
Система ограничений:
x11 x21 x31 15,x12 x22 x32 5,
x13 x23 x33 10,x14 x24 x34 10,
x11 x12 x13 x14 25,
x21 x22 x23 x24 25,x31 x32 x33 x34 20,
xmn ≥ 0.
Решение
Введем исходные данные и таблицу с изменяемыми ячейками в Excel, как и в транспортной задаче (рис. 3.30). При этом для каждого предприятия-поставщика берется вариант с максимальной мощностью: а1 – 25 т, а2 – 25 т, а3 – 20 т. Суммарная мощность составит 70 т. Тогда спрос фиктивного потребителя равен 30 т (предложение 70 т минус спрос 40 т). В первой таблице указаны затраты на производство и доставку одной тонны продукта, мощность поставщиков и потребности заказчиков.
150
