
Оптимизация в среде MATLAB
..pdfваться только когда число уравнений равно числу неизвестных. При выборе другого алгоритма его следует указать в параметре Algorithm.
Синтаксис обращения к функции fsolve:
x = fsolve(fun,x0)
x = fsolve(fun,x0,options) x = fsolve(problem) [x,fval] = fsolve(fun,x0)
[x,fval,exitflag] = fsolve(...) [x,fval,exitflag,output] = fsolve(...) [x,fval,exitflag,output,jacobian] = fsolve(...).
Входной аргумент fun – это имя m-файла, в котором вычисляется F(x) и, возможно, Якобиан. Последний представляет собой матрицу, строками которой являются градиенты Fi(x). Якобиан также может быть выходным аргументом (в последнем варианте обращения). Индикатор останова exitflag может принимать значения:
1– установлена сходимость к х;
2– изменение х меньше допустимой величины;
3– изменение невязки меньше допустимой величины;
4– величина направления поиска меньше заданной;
0 – число итераций или вычислений функции превысило максимально допустимое;
-1 – останов по причине функции вывода; -2 – алгоритм сходится к точке, не являющейся корнем;
-3 – радиус доверительной области стал слишком малым; -4 – невозможно существенно уменьшить невязку в направлении
текущего поиска. Структура output содержит поля, стандартные для рассматриваемых алгоритмов.
Параметры функции fsolve, общие и индивидуальные для алгоритмов, приведены в прил. 9. С их помощью можно влиять на процесс решения. При выборе алгоритма Levenberg-Marquardt можно также изменить его внутренний параметр , который по умолчанию равен 0,01, указав его в значении Algorithm за именем алгоритма, например
{'levenberg-marquardt',.003}.
Пример 27.
1. Решить систему
2x1x2 x2 e x1 e x2 ,x1 2x1x2 e x2 e x1 .
161
Перепишем эту систему в требуемой форме:
2x1x2 x2 e x1 e x2 0,x1 2x1x2 e x2 e x1 0.
Составим функцию для вычисления левых частей системы:
function F = equ(x) F=[2*x(1)*x(2)-x(2)-exp(-x(1))+exp(-x(2)); x(1)-2*x(1)*x(2)-exp(-x(2))+exp(-x(1))];
Задав начальную точку, запускаем решение:
>>x0=[1 1];[x,fval,exit]=fsolve(@equ,x0) Equation solved.
x =
0.5000 0.5000 fval =
1.0e-009 * / общий множитель
0.1164 -0.1164
exit =
1
Результаты показывают, что решение системы получено с высокой точностью (значения обеих функций практически равны нулю).
2. Решить систему, заданную в матричном виде:
6 |
2 |
|
X × X – 0,5X = |
4 |
. |
1 |
|
|
Сначала записываем m-файл, содержащий вычисляемую функцию:
function F =equ2(x) F=x*x-0.5*x-[6 2;1 4];
Затем выбираем в качестве решателя алгоритм LevenbergMarquardt, задаем начальную точку x0 с нулевыми значениями элементов и запускаем программу:
>>x0=zeros(2,2); options=optimset('Algorithm','levenberg-marquardt'); [x,fval,exit, output]=fsolve(@equ2,x0,options)
Equation solved. x =
-2.1914 -0.4513
162
-0.2257 -1.7401
fval = 1.0e-010 *
0.1295 0.1672
0.0682 -0.0274
exit =
1
output =
iterations: 5 funcCount: 32 stepsize: 1.1077e-007 cgiterations: []
firstorderopt: 7.6386e-011 algorithm: 'Levenberg-Marquardt' message: [1x685 char]
Как видим, система имеет решение и получено оно за пять итераций. Погрешность найденного решения (fval) пренебрежимо мала.
Если система уравнений линейная AX = B и число уравнений равно числу переменных, решение получить проще, используя оператор левого матричного деления \, т.е. имеем X = A\B. Эта формула справедлива, так как в рассматриваемом случае A\ дает обратную матрицу A–1.
Пример 28.
Решить систему уравнений
8x1 – 3x2 x3 6,4x1 5x2 2x3 13,
–7x1 x2 9x3 5.
Решение:
>> A=[8 -3 1;4 5 -2;-7 1 9]; B=[6;13;5]; X=A\B
Сразу получаем ответ:
X=
1.3534
2.0686
1.3784
163
9.3. Нелинейная задача наименьших квадратов
Задача состоит в минимизации суммы квадратов функций
n
F(x) fi (x)2
i 1
при условии lb x ub.
Для решения этой задачи предназначена функция lsqnonlin. Основные алгоритмы, используемые в ней: рефлексивный алгоритм дове-
рительных областей (trust-region-reflective algorithm) и алгоритм Левенберга – Марквардта (Levenberg-Marquardt algorithm).
Первый алгоритм, установленный по умолчанию, применим, когда размерность F не меньше числа переменных, а второй алгоритм неприменим при наличии границ на переменные. Для обоих алгоритмов необходимо, чтобы функции fi(x) были непрерывными. Параметры этих алгоритмов рассматривались ранее.
Синтаксис вызова функции lsqnonlin: x = lsqnonlin(fun,x0)
x = lsqnonlin(fun,x0,lb,ub)
x = lsqnonlin(fun,x0,lb,ub,options) x = lsqnonlin(problem)
[x,resnorm] = lsqnonlin(...) [x,resnorm,residual] = lsqnonlin(...) [x,resnorm,residual,exitflag] = lsqnonlin(...)
[x,resnorm,residual,exitflag,output] = lsqnonlin(...) [x,resnorm,residual,exitflag,output,lambda] = ...
lsqnonlin(...) [x,resnorm,residual,exitflag,output,lambda,...
jacobian] = lsqnonlin(...)
Большинство входных и выходных аргументов функции имеют тот же смысл, что и в ранее рассмотренных функциях. Заметим, что под fun понимается функция, вычисляющая все fi(x). Новыми выходными аргументами являются resnorm и residual. Первый из них – это значение F(x) в оптимальном решении, а residual – остатки, т.е. значения fi(x) в оптимальном решении.
164
Пример 29.
Найти минимум функции
F(x) = (6 – x1)2 + (x1 – 2)2 + (x2 – 1)2 + (x2 – 3)2.
Для решения этой задачи записываем m-функцию function f=squar(x) f(1)=6-x(1);
f(2)=x(1)-2; f(3)=x(2)-1; f(4)=x(2)-3;
и, задав начальную точку, вызываем функцию lsqnonlin:
>> x0=[1 1];[x,resnorm,residual] = lsqnonlin(@squar,x0)
Local minimum found. / найден локальный минимум x =
4 2 resnorm =
10 / значение F(x) residual =
2 2 1 -1 / значения f(1), f(2), f(3), f(4)
Пример 30.
Найти минимум функции
5
F(x) (3x1 x2ekx1 x1ekx2 5k)2 .
k 1
Решение:
1.Записываем m-файл function F=squar1(x) k=1:5;
F=3*x(1)-x(2)*exp(k*x(1))+x(1)*exp(k*x(2))-5*k;
2.Вызываем функцию lsqnonlin из выбранной начальной точки:
>>x0=[-2 0];[x,resnorm,residual] = lsqnonlin(@squar1,x0)
Local minimum possible. / возможно, найден локальный минимум
x =
0.3425 -4.5046 resnorm =
10.1099 residual =
2.3758 -0.0365 -1.3867 -1.2459 0.9946
165
9.4. Задача аппроксимации
Рассматривается следующая задача: имеется множество данных, отражающих неизвестную зависимость, и необходимо подобрать функцию (или функции), наиболее близкую к этим данным. Обычно эта задача решается так: задают вид функции, а ее параметры подбираются методом наименьших квадратов (в этом случае говорят о задаче подгонки кривой). Такой вариант решения реализует функция lsqcurvefit.
Формулировка задачи: найти такие коэффициенты x, при которых выражение
(F(x, xdatai ) ydatai )2
i
достигает минимума. Здесь xdatai и ydatai – известные входные и наблюдаемые выходные данные, а F – некоторая принятая функция с неизвестными коэффициентами x. Возможно также задание границ в виде lb x ub. Алгоритмы, используемые в lsqcurvefit, такие же, как в функции lsqnonlin.
Синтаксис вызова функции lsqcurvefit: x = lsqcurvefit(fun,x0,xdata,ydata)
x = lsqcurvefit(fun,x0,xdata,ydata,lb,ub)
x = lsqcurvefit(fun,x0,xdata,ydata,lb,ub,options) x = lsqcurvefit(problem)
[x,resnorm] = lsqcurvefit(...) [x,resnorm,residual] = lsqcurvefit(...) [x,resnorm,residual,exitflag] = lsqcurvefit(...) [x,resnorm,residual,exitflag,output] = ...
lsqcurvefit(...) [x,resnorm,residual,exitflag,output,lambda] = ...
lsqcurvefit(...) [x,resnorm,residual,exitflag,output,lambda,...
jacobian] = lsqcurvefit(...)
Используемые здесь входные и выходные аргументы не требуют пояснений, так как уже встречались ранее. Заметим только, что под fun понимается функция F(x, xdata), а не минимизируемое выражение.
166
Пример 31.
Получены данные измерений входной и выходной величины чер-
ного ящика. Значения на входе: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15; на выходе: 1,79, 3,22, 4,10, 4,83, 5,21, 5,25, 4,85, 4,50, 4,05, 3,31, 2,70, 2,00, 1,45, 0,75, 0,29. Требуется описать зависимость выхода от входа в классе функций F(x) k sin( x)e x .
Очевидно, что в такой постановке задача сводится к нахождению неизвестных коэффициентов функции k, α и . Сначала для вычисления значений заданной функции создаем m-файл:
function F=squar2(x,xdata) F=x(1)*sin(x(2)*xdata).*exp(x(3)*xdata);
где искомые коэффициенты обозначены как x(1), x(2) и x(3) соответственно.
Затем исполняем программу:
>> x0=[5; 1; -0.5];xdata=[1 2 3 4 5 6 7 8 9 10 11 12 13 14 15]; ydata=[1.79 3.22 4.10 4.83 5.21 5.25 4.85 4.50 4.05 3.31 2.70 2.00 … 1.45 0.75 0.29];
[x,resnorm] = lsqcurvefit(@squar3,x0,xdata,ydata)
Local minimum possible. x =
9.8913
0.2016 -0.0975
resnorm = 0.0467
Из отчета следует, что k = 9,8913, α = 0,2016 и = –0,0975. Значе-
ние resnorm и рис. 41 показывают, что полученная функция F(x) 9,8913sin(0,2016x)e 0,0975x хорошо аппроксимирует представленные данные.
167
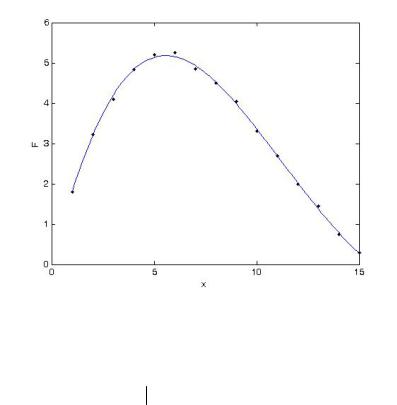
Рис. 41. Аппроксимация данных подходящей функцией
9.5. Неотрицательный линейный метод наименьших квадратов
Постановка задачи:
|
Cx d |
|
|
|
2 |
min |
|
|
|
||||
|
|
|
|
|
2 |
x |
|
|
|
|
|
при условии x 0. Предполагается, что система недоопределена или переопределена, т.е. число строк не равно числу переменных.
Для решения этой задачи предназначена функция lsqnonneg. Решение ищется с использованием базисных векторов и нахождением ассоциированных с ними элементов lambda. На каждой итерации базисный вектор, которому соответствует наибольшее значение lambda, заменяется небазисным. Решение завершается, когда lambda 0.
Синтаксис вызова lsqnonneg: x = lsqnonneg(C,d)
x = lsqnonneg(C,d,options) x = lsqnonneg(problem)
[x,resnorm] = lsqnonneg(...) [x,resnorm,residual] = lsqnonneg(...) [x,resnorm,residual,exitflag] = lsqnonneg(...)
[x,resnorm,residual,exitflag,output] = lsqnonneg(...) [x,resnorm,residual,exitflag,output,lambda] = ...
lsqnonneg(...)
168
Смысл всех обозначений очевиден. Элементы lambda(i) 0, когда x(i) = 0, и равны нулю при x(i) > 0.
Пример 32.
Найти решение задачи неотрицательных наименьших квадратов с тремя переменными и четырьмя равенствами при следующих C и d:
5 |
3 |
2 |
|
15 |
|||
|
|
|
|
|
|
|
|
C 6 |
|
9 |
1 |
, |
d 9 |
. |
|
|
|
8 |
3 |
|
|
|
|
4 |
|
|
4 |
|
|||
10 5 7 |
|
|
11 |
||||
Введя исходные данные и обратившись к функции lsqnonneg, получаем
>> C=[5 -3 2;6 9 -1;4 8 3;10 5 -7]; d=[15;9;4;11];
[x,resnorm] = lsqnonneg(C,d) x =
1.6623
0
0.7264 resnorm =
51.0769
Если снять ограничение неотрицательности переменных, то решение можно получить с помощью оператора левого матричного деления \. Для нашего примера имеем
>> C=[5 -3 2;6 9 -1;4 8 3;10 5 -7]; d=[15;9;4;11]; x=C\d
Получаем решение: x =
2.1397 -0.6322 0.8747
Подсчитаем resnorm=(C*x-d)'*(C*x-d)=13.6183 (' – символ транс-
понирования). Как видим, решение существенно улучшилось за счет возможности более широкого выбора значений переменных.
169

9.6.Линейная задача наименьших квадратов
сограничениями
Рассмотренная выше задача является частным случаем более общей задачи, модель которой имеет вид
1Cx d 2 min
22 x
при условиях
A x b, Aeq x = beq, lb x ub.
В такой постановке задача решается с помощью функции пакета lsqlin. При отсутствии равенств и неравенств и числе строк матрицы C не меньше числа столбцов применяется алгоритм Large Scale, основанный на subspace trust-region method. Этот алгоритм установлен по умолчанию. Если указанные условия не выполняются или алгоритм Large Scale выключен (опция 'off'), решение ищется алгоритмом Medium Scale как в функции quadprog. Параметры функции lsqlin аналогичны ранее рассмотренным параметрам для таких алгоритмов.
Синтаксис обращения к функции lsqlin:
x = lsqlin(C,d,A,b)
x = lsqlin(C,d,A,b,Aeq,beq)
x = lsqlin(C,d,A,b,Aeq,beq,lb,ub)
x = lsqlin(C,d,A,b,Aeq,beq,lb,ub,x0)
x = lsqlin(C,d,A,b,Aeq,beq,lb,ub,x0,options) x = lsqlin(problem)
[x,resnorm] = lsqlin(...) [x,resnorm,residual] = lsqlin(...) [x,resnorm,residual,exitflag] = lsqlin(...)
[x,resnorm,residual,exitflag,output] = lsqlin(...) [x,resnorm,residual,exitflag,output,lambda] = ...
lsqlin(...)
Входные аргументы функции описывают задачу, а выходные аргументы здесь те же, что в функции lsqnonneg. Положительные значения exitflag говорят о нормальном завершении поиска решения.
170
