m33751_5
.doc
1. Установить
вид частного
решения
с неопределенными коэффициентами по
виду функции
,
стоящей в правой части уравнения (3.4).
Для этого требуется:
1.1.
Составить характеристическое уравнение
и найти его корни
и
.
1.2. Определить по функции (3.6) число и сравнить его с и .
1.3.
Положить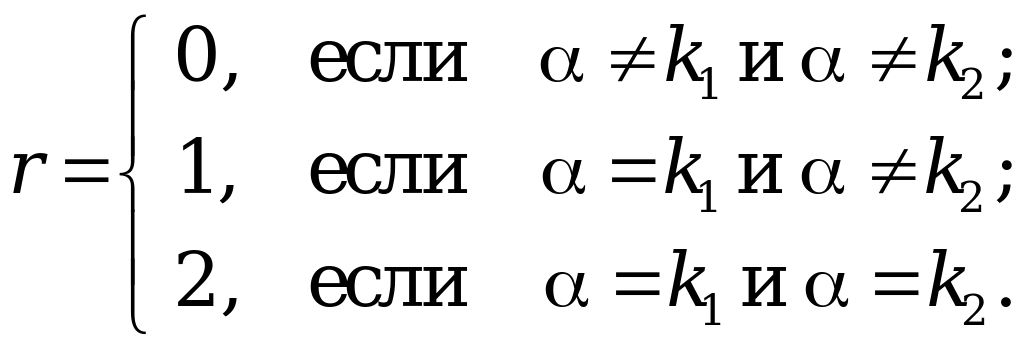 
1.4. Определить порядок n многочлена в функции (3.6) и записать частное решение в виде
, (3.7)
где
коэффициенты
,
,
,
…,
– не определены.
2. Отыскать значения неопределенных коэффициентов так, чтобы выражение (3.7) действительно являлось решением уравнения (3.4).
Для этого требуется:
2.1. Продифференцировать функцию (3.7) два раза, учитывая, что коэффициенты , , , …, являются константами.
2.2.
Подставить выражение для
и двух ее производных в исходное
дифференциальное уравнение (3.4). После
сокращения на
произвести приведение подобных и
группировку слагаемых по степеням x.
2.3. Приравнивая коэффициенты при одинаковых степенях х в левой и правой частях полученного уравнения, перейти к системе уравнений относительно неизвестных коэффициентов , , , …, . Решить систему уравнений и записать частное решение в форме (3.7) с найденными значениями коэффициентов.
Задание 6. Найти общее решение линейных неоднородных дифференциальных уравнений второго порядка.
Вариант 6.1 |
Вариант 6.2 |
Вариант 6.3 |
1.
|
1.
|
1.
|
2.
|
2.
|
2.
|
;
;
;
.
.
.
Вариант 6.4 |
Вариант 6.5 |
Вариант 6.6 |
1.
|
1.
|
1.
|
2.
|
2.
|
2.
|
;
;
;
.
.
.
Вариант 6.7 |
Вариант 6.8 |
Вариант 6.9 |
1.
|
1. |
1.
|
2.
|
2.
|
2.
|
;
;
;
.
.
.
Вариант 6.10 |
Вариант 6.11 |
Вариант 6.12 |
1.
|
1.
|
1.
|
2.
|
2.
|
2.
|
;
;
;
.
.
.
Вариант 6.13 |
Вариант 6.14 |
Вариант 6.15 |
1.
|
1.
|
1.
|
2.
|
2.
|
2.
|
;
;
;
.
.
.
Вариант 6.16 |
Вариант 6.17 |
Вариант 6.18 |
1.
|
1.
|
1.
|
2.
|
2.
|
2.
|
;
;
;
.
.
.
Вариант 6.19 |
Вариант 6.20 |
Вариант 6.21 |
1.
|
1.
|
1.
|
2.
|
2.
|
2.
|
;
;
;
.
.
.
Вариант 6.22 |
Вариант 6.23 |
Вариант 6.24 |
1.
|
1.
|
1.
|
2.
|
2.
|
2.
|
;
;
;
.
.
.
Вариант 6.25 |
Вариант 6.26 |
Вариант 6.27 |
1. ; |
1.
|
1.
|
2. . |
2.
|
2.
|
;
;
.
.
Вариант 6.28 |
Вариант 6.29 |
Вариант 6.30 |
1.
|
1.
|
1.
|
2.
|
2.
|
2.
|
;
;
;
.
.
.Решение типовых примеров
Пример 3.6. Найти общее решение линейного неоднородного дифференциального уравнения второго порядка
.
Решение.
1. Составим характеристическое уравнение
.
Дискриминант
.
Корни характеристического уравнения
– действительные и равные. Следовательно,
общее решение однородного уравнения,
соответствующего исходному, имеет вид
. (3.8)
2. В
правой части исходного неоднородного
уравнения имеется множитель
.
Число 0,
– не совпадает ни с одним из корней
характеристического уравнения,
следовательно r 0.
В
правой части также имеется множитель
следовательно, частное решение будет
содержать многочлен 2-го порядка с тремя
неизвестными коэффициентами
.
Укажем вид частного решения, подставляя известные параметры в шаблон (3.7)
.
3. Для определения неизвестных коэффициентов , , дважды продифференцируем полученную форму частного решения
,
.
Подставим
выражения для
,
,
в исходное дифференциальное уравнение.
После группировки по степеням x
получим следующее уравнение
,
от которого, приравнивая коэффициенты при одинаковых степенях x, можно перейти к следующей системе уравнений
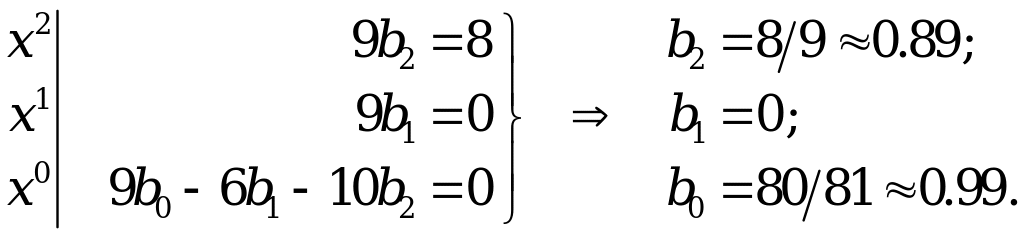
В результате, частное решение неоднородного дифференциального уравнения записывается в виде
. (3.9)
4. Таким образом, искомое общее решение запишется как сумма общего решения однородного (3.8) и частного решения неоднородного дифференциального уравнения (3.9)
.
Пример 3.7. Найти общее решение линейного неоднородного дифференциального уравнения второго порядка
.
Решение.
1. Составим характеристическое уравнение
.
Дискриминант . Корни характеристического уравнения – действительные и равные. Следовательно, общее решение однородного уравнения, соответствующего исходному, имеет вид
. (3.10)
В
правой части исходного неоднородного
уравнения имеется множитель
.
Число 3,
– совпадает с двумя корнями
характеристического уравнения,
следовательно r 2.
2. В правой части также имеется множитель 2 следовательно, частное решение будет содержать многочлен 0-го порядка с одним неизвестным коэффициентом .
Укажем вид частного решения, подставляя известные параметры в шаблон (3.7)
.
3. Для определения неизвестного коэффициента дважды продифференцируем полученную форму частного решения
,
.
Подставим выражения для , , в исходное дифференциальное уравнение. После сокращения общего множителя получим следующее уравнение
,
,
из
которого, после приведения подобных,
можно найти значение неизвестного
коэффициента
.
В результате, частное
решение неоднородного дифференциального
уравнения записывается в виде
. (3.11)
4. Таким образом, искомое общее решение запишется как сумма общего решения однородного (3.10) и частного решения неоднородного дифференциального уравнения (3.11)
.
ТЕМА 4. Классическое определение вероятности
Прежде чем приниматься за решение задач следует прочно усвоить следующие основные понятия темы.
Под испытанием понимается осуществление определенного комплекса условий, при которых производится наблюдение (опыт).
Событие – это качественный результат испытания. События обозначают: A, B, C, …
Достоверным называют событие, которое при данном испытании не может не произойти, т. е. наступает при каждом испытании. Обозначается достоверное событие . Событие называют невозможным, если при данном испытании оно не может произойти, оно обозначается как .
Случайным называют событие, которое при данном испытании может либо произойти, либо не произойти.