ТЕМА 6. ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ

В ЗАДАЧАХ 61 - 70 исследовать заданные функции методами дифференциального исчисления, начертить их графики. Исследование функции и построение графика рекомендуется проводить по следующей схеме:

1) найти область определения функции ;

2) исследовать функцию на непрерывность, найти точки разрыва функции и ее односторонние пределы;

3) найти точки экстремума функции и определить интервалы ее монотонности;

4) найти точки перегиба графика функции и определить интервалы выпуклости и вогнутости графика;

5) найти асимптоты графика функции;

6) построить график, используя результаты предыдущих исследований;

7) для функции из пункта найти дополнительно наибольшее и наименьшее значения на отрезке .

61.

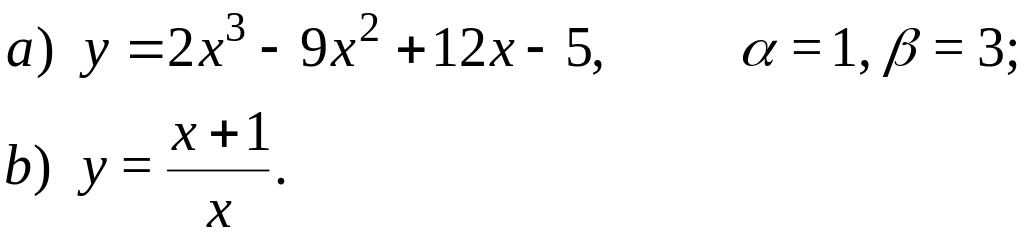
62.

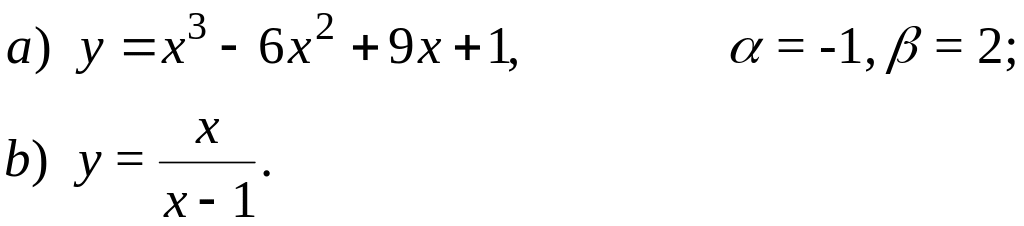
63.

64.

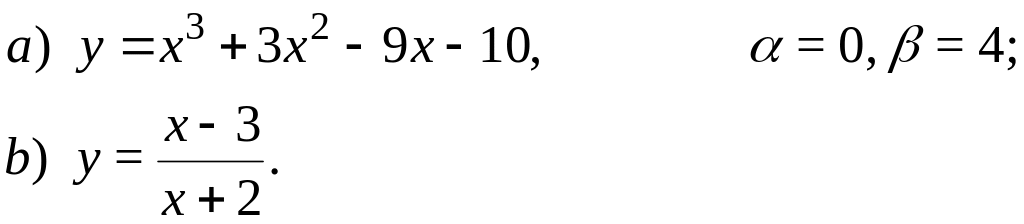
65.

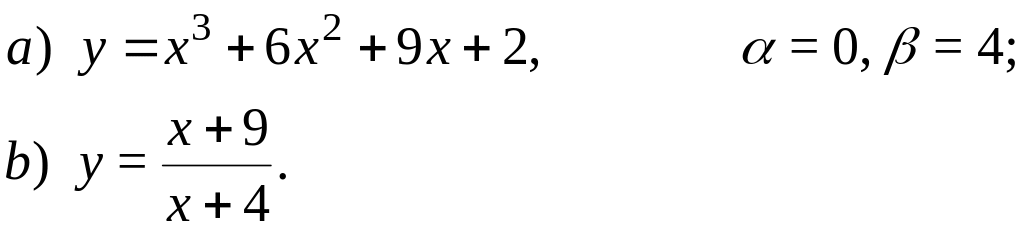
66.

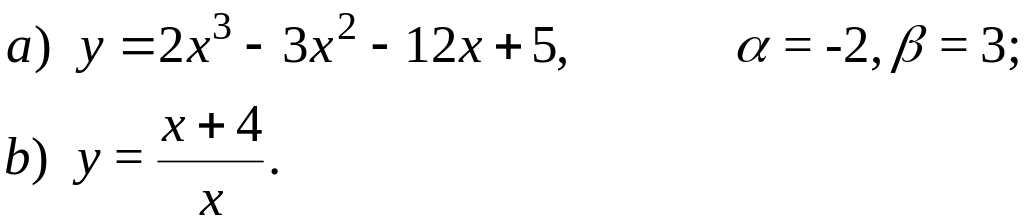
67.

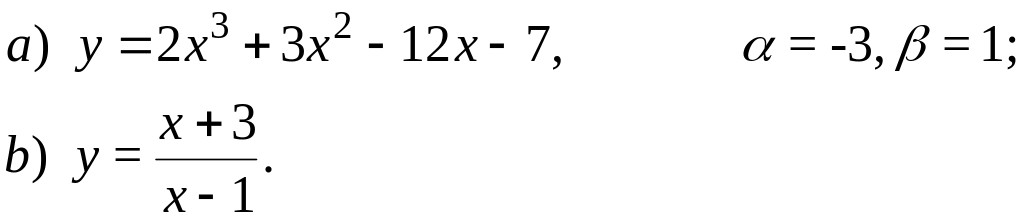
68.

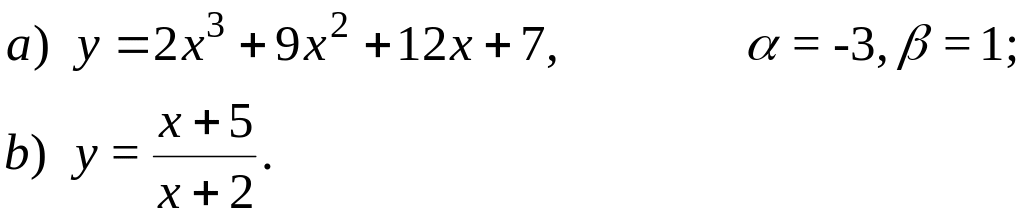
69.

70. 

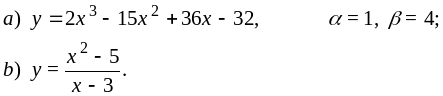
РЕШЕНИЕ ТИПОВОГО ПРИМЕРА.

1. .

Решение.

1) Областью определения данной функции являются все действительные значения аргумента , то есть , а это значит, что функция непрерывна на всей числовой прямой и ее график не имеет вертикальных асимптот.

2) Исследуем функцию на экстремум и интервалы монотонности. С этой целью найдем производную функции и приравняем ее к нулю:

.

Решая полученное квадратное уравнение, делаем вывод о том, что функция имеет две критические точки 1-го рода . Разбиваем область определения этими точками на части и по изменению знака производной в них выявляем промежутки монотонности и наличие экстремума:

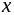
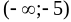
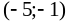
		-5		-1
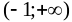
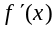
	+	0	–	0	+
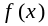
		max		min

;

.

Определим точки перегиба графика функции и интервалы его выпуклости и вогнутости. Для этого найдем вторую производную и приравняем ее к нулю:

.

Итак, функция имеет одну критическую точку 2-го рода . Разобьем область определения полученной точкой на интервалы, в каждом из которых установим знак второй производной:

		-3
	–	0	+
		точка перегиба

Значение является абсциссой точки перегиба графика функции, а ордината этой точки

.

4) Выясним наличие у графика заданной функции наклонных асимптот. Для определения параметров уравнения асимптоты воспользуемся формулами

; .

Имеем

.

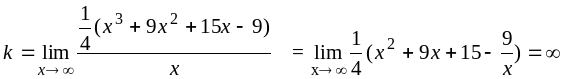Таким образом, у графика заданной функции наклонных асимптот нет.

5) Для построения графика в выбранной системе координат изобразим точки максимума , минимума , перегиба и точку пересечения графика с осью . С учетом результатов предыдущих исследований построим кривую (см. рис. 2).

6) Найдем наибольшее и наименьшее значения заданной функции на отрезке [-3,0]. Для этого посчитаем значения функции на концах этого отрезка, в критических точках 1-го рода, попавших на отрезок и сравним результаты:

.

Очевидно, что

.

y

A

				C
			-5	-3 -1				x
					D
				B

Рис. 2

ТЕМА 7. ПРИМЕНЕНИЕ ТЕОРИИ ЭКСТРЕМУМА

ДЛЯ НАХОЖДЕНИЯ НАИБОЛЬШИХ И

НАИМЕНЬШИХ ЗНАЧЕНИЙ ФУНКЦИЙ

РЕШИТЬ СЛЕДУЮЩИЕ ЗАДАЧИ

71. Канал, ширина которого 27 м, под прямым углом впадает в другой канал шириной 64 м. Какова наибольшая длина бревен, которые можно сплавлять по этой системе каналов?

72. Найти наибольший объем цистерны, для которой полная поверхность равна (м²).

73. Найти наибольший объем емкости в виде конуса, образующая которого равна (м).

74. Объем правильной треугольной призмы равен V=16 (м³). Какова должна быть длина стороны основания призмы, чтобы ее полная поверхность была наименьшей?

75. Открытый чан для воды имеет форму цилиндра объема (м³). Каковы должны быть радиус основания и высота чана, чтобы на его изготовление ушло наименьшее количество материала?

76. Требуется изготовить коническую воронку для слива с образующей, равной 20 см. Какова должна быть высота воронки, чтобы ее объем был наибольшим?

77. Требуется изготовить емкость для воды с крышкой, объем которой был бы равен 72 (м³), причем стороны основания относились как 1:2. Каковы должны быть размеры всех сторон, чтобы полная поверхность была наименьшей?

78. Сечение оросительного канала имеет форму равнобочной трапеции, боковые стороны которой равны меньшему основанию. При каком угле наклона боковых сторон сечение канала будет иметь наибольшую площадь?

79. Требуется изготовить бак, имеющий форму кругового конуса заданной вместимости (м³). Каковы должны быть размеры конуса, чтобы на бак ушло наименьшее количество материала?

80. Из прямоугольного листа жести размером 24х9 м требуется изготовить открытую емкость для воды, вырезая по углам листа равные квадраты и загибая оставшиеся боковые полосы под прямым углом. Какова должна быть сторона вырезаемых квадратов, чтобы вместимость коробки была наибольшей?

РЕШЕНИЕ ТИПОВОЙ ЗАДАЧИ

Задача. Среди емкостей в виде цилиндров, полная поверхность которых равна (м²), найти цилиндр, имеющий наибольший объем.

Решение. Пусть радиус основания цилиндра равен , а высота . Тогда полная поверхность

,

откуда

,

то есть объем цилиндра может быть выражен следующим образом:

.

Исследуем полученную функцию на максимум при .

Имеем . Решая уравнение, получаем

.

Так как при выполнено условие , то объем имеет наибольшее значение. При этом

,

поэтому искомые значения радиуса основания и высоты цилиндра равны соответственно 1 и 2.

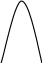
38