
5665
.pdf
надлежит. Интервал (9,4; 10,6) относительно точки xв |
10 имеет радиус |
0,6 . Та- |
ким образом, он может быть доверительным интервалом для оценки a . |
|
|
Ответ: доверительным интервалом для оценки M X |
при xв 10 из указанных ин- |
|
тервалов может быть только интервал (9,4; 10,6). |
|
|
Пример 21. По выборке 25 упаковок товара из генеральной совокупности, подчинённой нормальному закону распределения, средний вес составил 99 г с выборочным средним квадратическим отклонением 3 г. Найти доверительные интервалы для сред-
него с надёжностью |
0,9 . |
Решение. При неизвестном стандарте 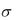 X
X 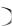 признак X генеральной совокупности с нормальным законом распределения, доверительным интервалом для математического ожидания a является интервал
признак X генеральной совокупности с нормальным законом распределения, доверительным интервалом для математического ожидания a является интервал
|
|
|
xв |
|
|
s |
|
|
t , |
xв |
|
|
|
s |
|
|
|
|
t |
|
(3.22) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
n |
1 |
|
|
n |
1 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
с центром в точке |
xв и радиусом |
|
|
|
s |
|
|
t , характеризующим точность (предель- |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
n |
1 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ную ошибку) интервальной оценки. Здесь |
|
|
s |
|
|
|
|
n |
|
, |
t – критическая точка рас- |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
в |
||||||||||||||||||
|
|
|
|
|
n |
1 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
пределения Стьюдента (для двусторонней области) с n |
|
1 степенью свободы и уров- |
||||||||||||||||||||||||||
нем значимости |
1 |
. По условию задачи |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
n |
25, |
xв |
99 , |
s |
|
|
n |
|
|
|
|
|
25 |
3 3,06 . |
||||||||||||||
n |
1 |
|
в |
24 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
В таблице критических точек распределения Стьюдента находим t 1,71 . Поэтому доверительный интервал для среднего (математического ожидания) имеет вид:
1,71 . Поэтому доверительный интервал для среднего (математического ожидания) имеет вид:
99 |
3,06 |
|
1,71; 99 |
3,06 |
|
1,71 или 97,932; 100,068 . |
|
||
|
|
|
|
|
|
|
|||
24 |
|
|
24 |
|
|
|
|||
|
|
|
|
|
|
||||
Ответ: доверительный интервал 97,932; 100,068 с надёжностью |
0,9 накрывает |
||||||||
неизвестное математическое ожидание.
Пример 22. Импортёр упаковывает чай в пакеты. Известно, что наполняющая машина работает нормально со средним квадратическим отклонением, равным 1 г, и средним выборочным весом пакетов 120 г. При каком минимальном объёме выборки с надёжностью 0,95 точность оценки математического ожидания составила бы 0,2 г?
Решение. Точность оценки математического ожидания нормально распределённой выборки при известном среднем квадратическом отклонении определяется формулой (3.19), то есть
u .
 n
n
81

|
2 |
|
|
|
|
|
|
|
|
Поэтому n |
|
u 2 , |
и так как по таблице функции Лапласа |
u |
0,95 / 2 0,475 , то |
||||
2 |
|||||||||
|
|
|
|
|
|
|
|
||
u 1,96 . Получим n |
1 |
3,8416 192 ,08 |
. Таким образом, |
минимальный объём вы- |
|||||
|
|
||||||||
0,04 |
|||||||||
борки будет равен 193. |
|
|
|
||||||
Ответ: минимальный объём выборки n |
193. |
|
|
||||||
Пример 23. Случайная выборка из 31 счёта дала значение исправленной диспер-
сии s 2 |
1,22 . Построить доверительный интервал для дисперсии всех счетов с надёж- |
||||||||||||||||||||||
ностью 0,95 в предположении нормальности генеральной совокупности. |
|
||||||||||||||||||||||
Решение. Доверительный интервал для неизвестной дисперсии 2 имеет вид: |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
n |
|
|
1 s 2 |
2 |
n 1 s 2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
(3.23) |
|||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
, n 1 |
|
|
1 |
|
, n 1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
||||||
где 2 |
, n 1 |
– критические точки |
|
2 -распределения со степенью свободы, равной n |
1, |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и соответствующим уровнем значимости |
1 . |
|
|
|
|
|
|
||||||||||||||||
В |
нашем случае |
|
1 |
0,95 |
|
0,05 . |
|
По |
таблице |
критических точек |
2 - |
||||||||||||
распределения имеем: |
2 |
|
47,0; |
|
|
|
2 |
|
16,8 . Тогда по формуле (3.23) |
|
|||||||||||||
0,025, 30 |
|
|
|
0,975, 30 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
30 |
1,22 |
2 |
|
30 |
|
1,22 |
, или 0,7788 |
2 |
|
2,1786 . |
|
|||||||||
|
|
47,0 |
|
|
16,8 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Ответ: доверительный интервал с надёжностью 0,95 для неизвестной дисперсии имеет вид 0,7788 ; 2,1786 .
Пример 24. Если устройство функционирует правильно, то вероятность прохождения теста равна 0,9; в противном случае, когда устройство функционирует неправильно, вероятность прохождения теста равна 0,4. Устройство допускается к работе, если тест проходит 4 раза подряд. В предположении, что тестирование производится независимо друг от друга, найти вероятности ошибок первого и второго родов.
Решение. Пусть основная гипотеза H 0 – устройство функционирует правильно, а альтернативная H1 – устройство работает неправильно. Тогда ошибкой первого рода
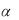 называют вероятность отклонить основную гипотезу, в то время как она верна. Такое происходит, когда прибор функционирует правильно, но тест четыре раза подряд
называют вероятность отклонить основную гипотезу, в то время как она верна. Такое происходит, когда прибор функционирует правильно, но тест четыре раза подряд
не проходит. |
Тогда, |
переходя к противоположному событию, получим |
||
P H |
1 |
1 |
0,94 1 |
0,6561 0,3439. |
H0 |
|
|
|
|
Ошибкой второго рода называют вероятность принять основную гипотезу, в то время как верна альтернативная. Это происходит тогда, когда неправильно функционирующее устройство проходит тест четыре раза подряд. Учитывая то, что тестиро-
вание |
проводится |
независимо друг от друга, получим ошибку второго рода |
|||
P |
H |
0 |
0,44 |
0,0256. |
|
H |
|
|
|
|
|
1 |
|
|
|
|
|
Ответы: |
0,3439 , |
0,0256. |
|||
|
|
|
|
|
82 |
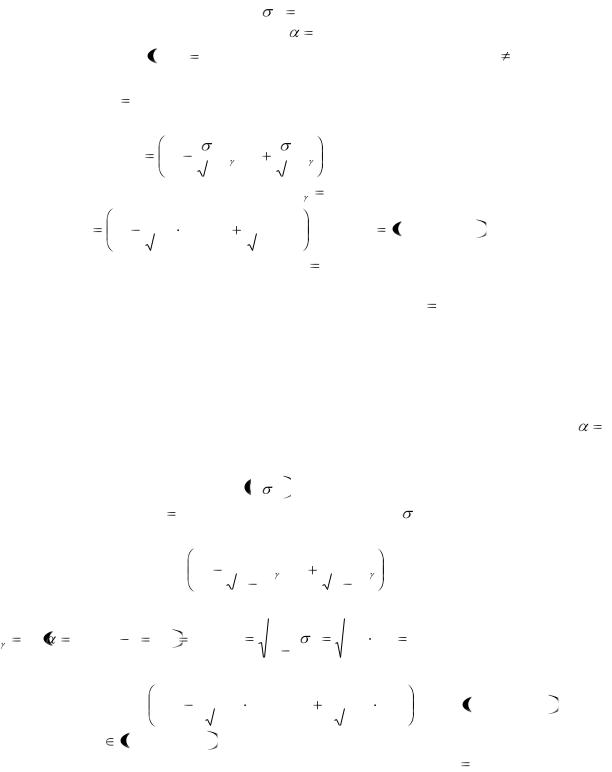
Пример 25. Выборка 25 единиц из генеральной совокупности, распределённой по
нормальному закону с дисперсией |
2 |
100, дала выборочную среднюю, равную 17. |
|
||
Можем ли мы при уровне значимости |
0,05 отклонить гипотезу о равенстве гене- |
|
ральной средней 20 H 0: a 20 при конкурирующей гипотезе H1 : a 20 ?
при конкурирующей гипотезе H1 : a 20 ?
Решение. Если в качестве статистики критерия проверки гипотезы взять выборочную среднюю Z xв , то областью принятия решения в данном случае будет довери-
тельный интервал, определяемый формулой (3.18):
|
W0 |
|
xв |
|
|
|
|
u , xв |
|
|
|
|
|
|
u . |
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
n |
|
|
|
||||
Как уже было найдено в примере 17, u |
1,96 ; поэтому |
||||||||||||||||||||
W |
17 |
10 |
|
|
1,96, 17 |
10 |
|
1,96 |
, или W |
|
13, 08; 20,92 . |
||||||||||
|
|
|
|
|
|
0 |
|||||||||||||||
0 |
|
25 |
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Как видим, гипотетическое значение a |
20 попадает в область принятия решения, |
||||||||||||||||||||
и отклонить основную гипотезу у нас нет оснований.
Ответ: нет оснований отклонить основную гипотезу a 20 .
Пример 26. Инвестиционный фонд объявил, что средний доход по акциям предприятий металлургической отрасли составил 11,5 %. Инвестор, желая проверить, является ли это заявление правильным, взял случайную выборку из 41 акции этой отрасли. Средний годовой доход по ним составил 10,8 % и выборочное среднее квадра-
тическое отклонение 3,4 %. Может ли инвестор при уровне значимости |
0,05 |
опровергнуть заявление инвестиционного фонда?
Решение. Будем считать, что значения доходов в металлургической отрасли имеют нормальное распределение N a, 2 . В качестве статистики критерия возьмём выборочную среднюю ( Z xв ). Тогда, так как дисперсия 2 нам неизвестна, то областью принятия решения будет доверительный интервал, определяемый формулой (3.22):
xв |
|
s |
|
|
t , xв |
|
s |
t . |
||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||
n |
1 |
n 1 |
||||||||
|
|
|
|
|
||||||
В данном случае из таблицы критических значений распределения Стьюдента:
t tкр |
0,05; n |
1 40 |
2,02 , s |
|
n |
|
|
|
|
|
|
41 |
|
|
3.4 |
3,4422 . Подставляя найденные |
||||||
|
n |
1 |
|
в |
40 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
значения, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
10,8 |
3,4422 |
2,02; 10,8 |
|
3,4422 |
2,02 |
, или |
9,701; 11,899 . |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
40 |
|
|
|
40 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Так как 11,5 |
9,701; 11,899 , то отклонить основную гипотезу у нас нет оснований. |
|||||||||||||||||||||
Ответ: нет оснований отклонить основную гипотезу, что a |
11,5% . |
|||||||||||||||||||||
Пример 27. Выборочные данные о числе сделок, заключённых брокерскими конторами города в течение месяца, приведены в таблице:
Число заключенных сделок |
0-10 |
|
10-20 |
20-30 |
30-40 |
40-50 |
Число брокерских контор |
23 |
|
24 |
11 |
9 |
3 |
|
|
83 |
|
|
|
|

Используя критерий согласия 2 Пирсона, проверить при уровне значимости |
0,05 |
гипотезу о нормальном законе распределения.
Решение. Для проверки гипотезы о нормальном распределении рассмотрим статистику критерия Пирсона
|
2 |
ni npi |
2 |
|
|
|
r |
|
|
|
|
|
|
|
|
, |
(3.24) |
|
i 1 |
npi |
|
||
|
|
|
|
||
где r |
– число интервалов разбиения вариационного ряда, ni |
– частоты вариационного |
|||
ряда, |
pi – теоретические вероятности попадания в соответствующий интервал вариа- |
||||
ционного ряда в предположении истинности основной гипотезы, n – объём выборки. Из равенства (3.24) видно, что критерий Пирсона сравнивает близость эмпириче-
ских (опытных) частот ni , попавших в случайную выборку, и так называемых теоретических частот npi , зависящих от теоретических вероятностей pi , которые, в свою
очередь, связаны с видом предполагаемого закона. Если выдвинутая гипотеза будет отвергаться, то расхождение между эмпирическими частотами и предполагаемыми теоретическими носит не случайный характер, говорят, что это расхождение значимо.
По критерию согласия Пирсона можно проверять гипотезы о разных законах (см. пример 28). При применении этого критерия обычно предъявляются следующие требования к выборке: n 50 , r 5 , ni 5 . Группы (частичные интервалы) с малочис-
ленными частотами присоединяют к соседним, суммируя частоты. При объединении
интервалов требование r |
5 к объединённому числу промежутков желательно сохра- |
нить. |
|
В данном примере n |
70, r 5 ; объединение промежутков не производим. |
Для нахождения теоретических вероятностей pi необходимо сначала, используя
формулы (3.13) и (3.15), оценить параметры нормального распределения. Для удобства расчётов воспользуемся вспомогательной таблицей расчётов
|
|
|
интервалы |
|
|
|
|
n |
i |
|
x |
i |
|
x |
n |
i |
x 2 n |
i |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
i |
|
|||||||
|
|
|
|
|
0-10 |
|
|
|
|
23 |
|
5 |
|
|
115 |
|
575 |
|
|||||||
|
|
|
|
|
10-20 |
|
|
|
|
24 |
|
15 |
|
360 |
|
5400 |
|
||||||||
|
|
|
|
|
20-30 |
|
|
|
|
11 |
|
25 |
|
275 |
|
6875 |
|
||||||||
|
|
|
|
|
30-40 |
|
|
|
|
9 |
|
35 |
|
315 |
|
11025 |
|
||||||||
|
|
|
|
|
40-50 |
|
|
|
|
3 |
|
45 |
|
135 |
|
6075 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
70 |
|
|
|
|
|
1200 |
|
29950 |
|
|||||
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi ni |
1200 |
|
|
|
|
|
|
|
|
29950 |
|
|
|
|
|||||
|
Тогда |
x |
|
|
i 1 |
17,14, |
|
D x2 |
x 2 |
|
17,142 133,98 , |
||||||||||||||
|
|
|
|
в |
|
n |
|
70 |
|
|
|
|
в |
|
|
|
|
|
70 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
11,57 . За xi принимались середины интервалов. Теперь можно вычислить |
||||||||||||||||||||||
в |
|
Dв |
|||||||||||||||||||||||
теоретические вероятности |
pi P ai |
X |
|
ai 1 . Так как предполагаем, что изучаемый |
|||||||||||||||||||||
признак распределён по нормальному закону, то надо применять формулу (2.30) из модуля 2, которая приобретёт вид:
84

|
|
|
|
|
|
|
|
|
|
|
|
P ai X ai 1 |
|
ai |
1 a |
|
|
|
|
ai |
a |
, |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
где |
x |
есть функция Лапласа. В этом равенстве неизвестные |
a |
( a |
|
M X ) и |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
X заменим их статистическими оценками: a |
|
xв , |
|
|
|
s |
|
|
|
|
n |
Dв |
. Таким об- |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
n |
1 |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
разом, |
pi |
будут вычисляться по формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
ai 1 |
xв |
|
|
|
ai |
|
|
|
xв |
. |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
s |
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Поскольку в данном примере поправочный множитель |
|
n |
|
70 |
1 |
, то s |
можно за- |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
n |
|
1 |
|
69 |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
менить на |
|
|
в . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычисления дадут следующие результаты: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
p1 |
|
10 |
17,14 |
|
|
|
0 |
17,14 |
|
|
0,62 |
|
|
1,48 |
|
0,23 |
0,43 |
|
|
0,2 , |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
11,57 |
|
|
|
|
|
|
11,57 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
p2 |
|
20 |
17,14 |
|
|
10 |
17,14 |
|
0,25 |
|
|
0,62 |
|
0,1 |
0,23 |
|
0,33, |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
11,57 |
|
|
|
|
|
|
11,57 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
p3 |
|
30 |
17,14 |
|
|
20 |
17,14 |
|
1,11 |
|
|
0,25 |
|
0,37 |
|
0,1 |
|
0,27 , |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
11,57 |
|
|
|
|
|
|
11,57 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
p4 |
|
40 |
17,14 |
|
|
30 |
17,14 |
|
1,98 |
|
1,11 |
|
0,48 |
|
0,37 |
|
0,11, |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
11,57 |
|
|
|
|
|
|
11,57 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
p5 |
|
50 |
17,14 |
|
|
40 |
17,14 |
|
2,84 |
|
|
1,98 |
|
0,5 |
|
0,48 |
|
0,02 . |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
11,57 |
|
|
|
|
|
|
11,57 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Чтобы рассчитать выборочное значение статистики |
2 |
|
по формуле (3.24), исполь- |
|||||||||||||||||||||||||||||||||||||||||||
зуем ещё одну вспомогательную таблицу: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
интервалы |
|
|
|
ni |
|
|
|
pi |
|
|
npi |
|
|
|
|
n |
|
|
np 2 |
|
|
|
|
n |
np |
2 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
i |
|
|
|
|
i |
|
|
i |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
npi |
|
|
|
|
|
||
|
|
0 - 10 |
|
|
|
23 |
|
0,174 |
|
12,18 |
|
|
117,0724 |
|
|
9,6118 |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
10 - 20 |
|
|
|
24 |
|
0,303 |
|
21,21 |
|
|
|
|
7,7841 |
|
|
|
0,3670 |
|
|
|
|
|
||||||||||||||||||||||
|
|
20 - 30 |
|
|
|
11 |
|
0,322 |
|
22,54 |
|
|
133,1716 |
|
|
|
5,9082 |
|
|
|
|
|
||||||||||||||||||||||||
|
|
30 - 40 |
|
|
|
|
|
|
9 |
|
0,102 |
|
|
7,14 |
|
|
|
|
|
|
7,14 |
|
|
|
|
0,4845 |
|
|
|
|
|
|||||||||||||||
|
|
40 - 50 |
|
|
|
|
|
|
3 |
|
0,035 |
|
|
2,45 |
|
|
|
|
|
|
2,45 |
|
|
|
|
0,1235 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
70 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
16,50 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Известно (см., например, [15], [18]), что статистика Пирсона имеет распределение хи-квадрат с k степенями свободы, где k r l 1. Здесь r – число интервалов разбиения вариационного ряда ( r 5 ), l – число параметров гипотетического закона распределения (для нормального закона l 2 ). По таблице критических значений распределения Пирсона при уровне значимости 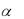 0,05 с двумя степенями свободы
0,05 с двумя степенями свободы
2 крит(0,05; 2)
6 .
85

Так как |
2 |
16,50 > |
2 |
6 , то гипотеза о нормальном распределении отвергается. |
в |
крит(0,05; 2) |
Ответ: при уровне значимости 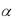 0,05 отвергаем гипотезу о нормальном распределении. Пример 28. Выборочные данные о числе сделок, заключённых брокерскими кон-
0,05 отвергаем гипотезу о нормальном распределении. Пример 28. Выборочные данные о числе сделок, заключённых брокерскими кон-
торами города в течение месяца, приведены в таблице:
|
Число заключенных сделок |
0-10 |
10-20 |
20-30 |
|
30-40 |
40-50 |
|
|
|
Число брокерских контор |
23 |
|
24 |
11 |
|
9 |
3 |
|
Используя критерий согласия 2 |
Пирсона, |
проверить при |
уровне |
значимости |
|||||
 0,05 гипотезу о показательном законе распределения.
0,05 гипотезу о показательном законе распределения.
Решение. Функция распределения для показательного закона распределения имеет вид
(2.26). Оценку параметра |
можно найти, например, методом моментов (см. (3.17)): |
||||||||
|
|
1 |
|
|
1 |
|
0,0584 . |
||
|
|
|
|
|
|
|
|
||
|
|
|
xв |
17,14 |
|||||
|
|
|
|
|
|||||
Выборочная средняя xв |
найдена в предыдущем примере. |
||||||||
Теоретические вероятности pi найдём, используя формулу (2.27): |
|||||||||
p |
1 |
e 0,0584 10 |
1 |
|
e 0.0584 0 |
0,4423 , |
|||
1 |
|
|
|
|
|
|
|
|
|
p2 |
1 |
e 0,0584 20 |
1 |
|
e 0.0584 10 |
0,2467 , |
|||
p3 |
1 |
e 0,0584 30 |
1 |
|
e 0.0584 20 |
0,1376 , |
|||
p4 |
1 |
e 0,0584 40 |
1 |
|
e 0.0584 30 |
0,0767 , |
|||
p5 |
1 |
e 0,0584 50 |
1 |
|
e 0.0584 40 |
0,0428 . |
|||
Вычислим выборочное |
значение статистики |
2 |
по |
формуле |
(3.24), используя |
|||||||||||||
вспомогательную таблицу, как в предыдущем примере: |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
интер- |
ni |
|
|
pi |
|
npi |
|
|
n |
np 2 |
|
|
n |
np 2 |
|
|
|
|
валы |
|
|
|
|
|
|
|
|
i |
i |
|
|
i |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
npi |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
0 - 10 |
23 |
|
0,4423 |
|
30,961 |
|
63,3776 |
|
2,0471 |
|
|
|||||
|
|
10 - 20 |
24 |
|
0,2467 |
|
17,269 |
|
45,3064 |
|
2,6236 |
|
|
|||||
|
|
20 - 30 |
11 |
|
0,1376 |
|
9,632 |
|
|
1,8715 |
|
0,1943 |
|
|
||||
|
|
30 - 40 |
9 |
|
0,0767 |
|
5,369 |
|
|
13,1842 |
|
2,4557 |
|
|
||||
|
|
40 - 50 |
3 |
|
0,0428 |
|
2,996 |
|
|
0,0001 |
|
0,0001 |
|
|
||||
|
|
|
70 |
|
|
|
|
|
|
|
|
|
|
2 |
7,3208 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Так как показательный закон имеет один параметр |
l 1 , а число групп данной |
|||||||||||||||||
выборки |
r 5 , то число степеней свободы k |
5 |
1 |
1 |
3. По таблице критических |
|||||||||||||
значений распределения Пирсона при уровне значимости |
0,05 и тремя степенями |
|||||||||||||||||
свободы |
2 |
7,8 . Так как |
2 |
7,3208 < |
2 |
|
|
7,8, |
то у нас нет оснований |
|||||||||
крит(0,05; 3) |
в |
крит(0,05; 2) |
||||||||||||||||
отвергнуть гипотезу о показательном законе распределении. |
|
|
|
|
|
|
||||||||||||
Ответ: нет оснований при уровне значимости |
|
0,05 отвергнуть гипотезу о пока- |
||||||||||||||||
зательном законе распределения.
86

Пример 29. В результате проверки 300 контейнеров со стеклянными стаканами установлено, что число повреждённых стаканов X имеет следующее эмпирическое распределение:
|
xi |
0 |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
|
|
|
|
mi |
50 |
100 |
80 |
40 |
20 |
10 |
|
Проверить при уровне значимости |
0,05 гипотезу о том, что случайная величи- |
|||||||
на X распределена по закону Пуассона.
Решение. Пуассоновский закон распределения имеет вид (2.16), где параметр 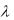 M X . Тогда в качестве оценки параметра можно взять выборочное среднее, рассчитанное по формуле (3.13):
M X . Тогда в качестве оценки параметра можно взять выборочное среднее, рассчитанное по формуле (3.13):
xв |
0 50 |
1 100 |
2 80 |
3 40 |
4 |
20 |
5 10 |
1,7 . |
|
|
|
|
|
|
|
|
|
||
|
|
|
300 |
|
|
|
|||
|
|
|
|
|
|
|
|
||
Проверку гипотезы H 0 |
о том, что распределение случайной величины X – числа |
||||||||
повреждённых стаканов будет пуассоновским, проведём по критерию согласия хи квадрат. Для вычисления выборочного значения статистики критерия применим фор-
мулу (3.24). Теоретические вероятности pi |
|
вычислим по формуле (2.16): |
||||||||||||||||||||||
|
|
|
p |
|
P |
X |
0 |
1,70 |
|
|
e 1,7 |
|
0,1827 , |
|
|
|
|
|
|
|||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
H 0 |
|
|
0! |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
p |
|
P |
X |
1 |
1,71 |
|
e 1,7 |
0,3106 , |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
1 |
H0 |
|
|
1! |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
p |
|
P |
X |
2 |
1,72 |
|
|
e 1,7 |
|
0,2640 , |
|
|
|
|
|
|
|||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
H0 |
|
|
2! |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
p |
|
P |
X |
3 |
1,73 |
|
e 1,7 |
|
0,1496 , |
|
|
|
|
|
|
||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
H0 |
|
|
3! |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
p |
|
P |
X |
4 |
1,74 |
|
|
e 1,7 |
|
0,0636 , |
|
|
|
|
|
|
|||||
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
H0 |
|
|
4! |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
p |
|
P |
X |
5 |
1,75 |
|
|
e 1,7 |
|
0,0216 . |
|
|
|
|
|
|
|||||
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
H0 |
|
|
5! |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Для вычисления |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
в используем вспомогательную таблицу: |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
xi |
|
ni |
|
|
pi |
|
|
npi |
|
|
|
|
n np 2 |
|
n np |
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
i |
|
|
|
i |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
npi |
|
|
|
0 |
|
50 |
|
0,1827 |
|
54,81 |
|
|
|
|
|
|
23,1361 |
|
|
0,4222 |
|
||||||
|
1 |
|
100 |
0,3106 |
|
93,18 |
|
|
|
|
|
|
46,5124 |
|
|
0,4992 |
|
|||||||
|
2 |
|
80 |
|
0,2640 |
|
79,20 |
|
|
|
|
|
|
0,64 |
|
|
0,0081 |
|
||||||
|
3 |
|
40 |
|
0,1496 |
|
44,88 |
|
|
|
|
|
|
23,8144 |
|
|
0,5307 |
|
||||||
|
4 |
|
20 |
|
0,0636 |
|
19,08 |
|
|
|
|
|
|
0,8464 |
|
|
0,0444 |
|
||||||
|
5 |
|
10 |
|
0,0216 |
|
6,48 |
|
|
|
|
|
|
12,3904 |
|
|
1,9121 |
|
||||||
|
|
|
300 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3,4167 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
87 |
|
|
|
|
|
|
|
|||

|
Так как r |
6 , l |
1, то k |
r |
l 1 4 . По таблице критических значений распреде- |
||
ления Пирсона при уровне значимости |
0,05 с четырьмя степенями свободы име- |
||||||
ем |
2 |
9,5. |
Так как |
2 |
3,4167 < |
2 |
9,5, то нет оснований отвергнуть |
крит(0,05; 4) |
в |
крит(0,05; 4) |
|||||
гипотезу о пуассоновском распределении числа повреждённых стаканов.
Ответ: нет оснований при уровне значимости  0,05 отвергнуть гипотезу о пуассоновском распределении числа повреждённых стаканов.
0,05 отвергнуть гипотезу о пуассоновском распределении числа повреждённых стаканов.
Пример 30. Уравнение парной регрессии Y на X , полученное по данным выбор-
ки, имеет вид |
y 2,5x 5,4 . Тогда выборочный коэффициент корреляции rв может |
|||||||
принять значение 1) 1,4; 2) 0,9; 3) -0,85; 4) -2,5. |
|
|
|
|
|
|
||
Решение. Значение выборочного коэффициента корреляции rв |
принадлежит про- |
|||||||
межутку |
1, 1 . Поэтому ответы 1) и 4) не верны. Согласно полученному уравнению |
|||||||
регрессии, |
коэффициент регрессии Y на X |
yx |
|
2,5 , то есть коэффициент отрица- |
||||
телен. Так как |
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
y |
, |
(3.25) |
|
|
|
yx |
|
|
|||
|
|
|
в |
|
||||
|
|
|
|
|
|
x |
|
|
то знаки rв |
и |
yx совпадают. Следовательно, rв |
может принять только значение 3). |
|||||
Ответ: возможен результат rв 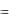 0,85 .
0,85 .
Пример 31. По данным выборки получены значение rв и значения выборочных среднеквадратических отклонений: rв 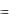 0,8 ; x 5,2; y 1,3 . Найти коэффициент yx ли-
0,8 ; x 5,2; y 1,3 . Найти коэффициент yx ли-
нейной регрессии Y на X .
Решение. Из данных примера и равенства (3.25) имеем
1,3
yx 0,8 5,2 0,2 .
Ответ: yx 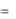 0,2 .
0,2 .
Пример 32. Дана таблица результатов наблюдений:
X |
2 |
4 |
6 |
8 |
10 |
Y |
3 |
6 |
7 |
6 |
8 |
Найти выборочный коэффициент корреляции.
Решение. Выборочный коэффициент корреляции определяется формулой
|
|
1 |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
xi yi xв yв |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
xy |
x y |
|
|
|||
rв X , Y |
|
|
i 1 |
|
|
, |
(3.26) |
|||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
Dв X Dв Y |
|
|
|
x |
y |
|||||
|
|
|
|
|
|
|
|
|
||||
где выборочные средние xв , yв рассчитываются по формуле (3.13), а выборочные дисперсии – по формуле (3.15):
xв |
1 |
2 4 6 8 10 |
30 |
6 ; yв |
1 |
3 6 7 6 8 |
30 |
6 ; |
|
5 |
5 |
5 |
5 |
||||||
|
|
|
|
|
|||||
|
|
|
|
88 |
|
|
|
|
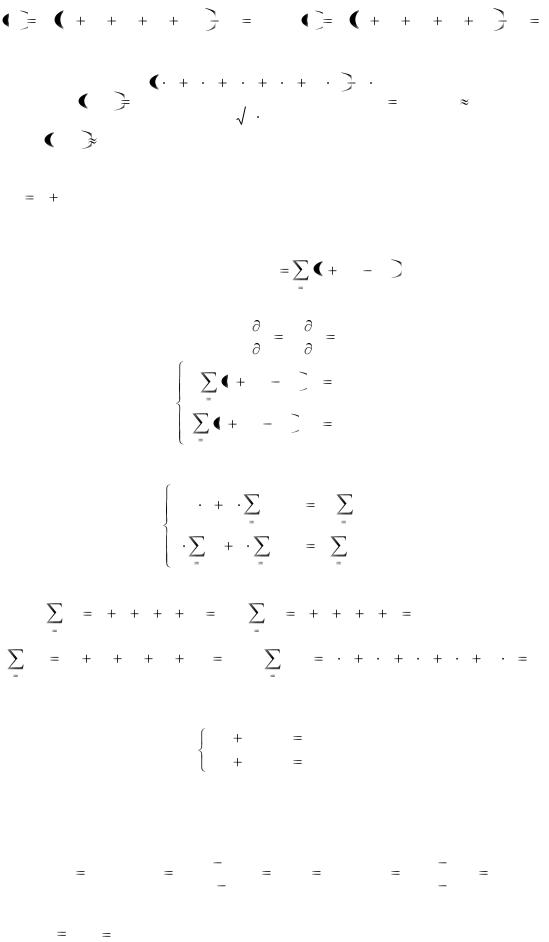
D X |
1 |
22 |
42 62 |
|
|
82 |
102 |
62 8 |
; D Y |
1 |
32 62 |
72 62 82 62 2,8 . |
||||||
|
|
|
|
|||||||||||||||
в |
5 |
|
|
|
|
|
|
|
|
|
в |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Подставляя найденные значения в формулу (3.26), получим |
|
|
||||||||||||||||
|
|
|
|
|
1 |
2 3 |
4 6 |
6 7 |
8 6 |
10 |
8 |
6 6 |
|
|
|
|||
|
|
|
|
|
|
|
4 |
|
||||||||||
|
|
rв |
X , Y |
|
5 |
0,98 . |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4,09878 |
|||
|
|
|
|
|
6 |
2,8 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ответ: rв |
X , Y |
0,98 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 33. В условиях предыдущего примера найти коэффициенты линейной регрессии y a bx .
Решение. Коэффициенты a и b найдём методом наименьших квадратов (МНК). Для этого составим функцию, равную сумме квадратов отклонений теоретических
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
2 . Найдём значения коэф- |
|
значений величины Y от фактических yi |
L |
|
|
|
a |
bxi |
yi |
|||||||||
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
фициентов a, b при условии, |
что при данных значениях функция достигает миниму- |
|||||||||||||||
ма. В такой точке частные производные |
|
|
L |
|
0, |
|
L |
|
0 . Получим систему уравнений: |
|||||||
|
|
a |
|
b |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
a |
bxi |
yi |
|
|
|
|
0, |
|
|
||||
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
a |
bxi |
|
yi |
xi |
|
|
0. |
|
|
||||
|
|
i |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Преобразуя данную систему, получим |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
5 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
a |
5 |
b |
|
|
xi |
|
|
|
|
|
yi , |
|
||
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
i 1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
5 |
|
|
|
5 |
|
2 |
|
|
|
|
5 |
|
|
|
|
|
a |
xi |
b |
|
|
|
xi |
|
|
|
|
yi xi . |
|
||
|
|
i |
1 |
|
|
i |
1 |
|
|
|
|
|
|
i 1 |
|
|
Так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
||
xi |
2 4 6 8 10 30 , |
|
|
yi |
|
3 6 7 6 8 30 , |
||||||||||
i 1 |
|
|
|
|
i |
1 |
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
xi 2 22 |
42 62 82 |
10 2 |
220 , |
|
|
xi |
yi |
|
|
2 3 |
4 6 |
6 7 8 6 10 8 200 , |
||||
i 1 |
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
то система примет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5a |
30b |
|
|
|
30, |
|
|
||||||
|
|
|
30a |
220b |
|
|
|
200. |
|
|
||||||
Данную систему двух линейных уравнений с двумя неизвестными можно решить методом Крамера:
|
|
30 |
30 |
|
|
|
|
|
|
|
|
5 |
30 |
|
|
|
|
|
|
a |
|
200 |
220 |
6600 |
6000 |
3 ; |
b |
|
30 |
200 |
1000 |
900 |
0,5 . |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
5 |
30 |
|
1100 |
900 |
|
5 |
30 |
1100 |
900 |
||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
30 |
220 |
|
|
|
|
|
|
|
|
30 |
220 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответы: a 3, b 0,5 .
89
Библиографический список
1.Айвазян С. А. Прикладная статистика. Основы моделирования и первичная обработка данных / С. А. Айвазян, И. С. Енюков, Л. Д. Мешалкин. – М. : Финансы и статистика, 1983. 471 с.
2.Вентцель Е. С. Теория вероятностей / Е. С. Вентцель. – М. : Наука, 1969. 576 с.
3.Гмурман В. Е. Теория вероятностей и математическая статистика / В. Е. Гмурман. – М. : Высшая школа, 1978. 368 с.
4.Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике / В. Е. Гмурман. – М. : Высшая школа, 1997. 400 с.
5.Гнеденко Б. В. Курс теории вероятностей / Б. В. Гнеденко. – М. : Наука, 1988. 448 с.
6.Коваленко И. Н. Теория вероятностей и математическая статистика / И. Н. Коваленко, А. А. Филиппова. – М. : Высшая школа, 1982. 256 с.
7.Колемаев В. А. Теория вероятностей и математическая статистика /В. А. Колемаев, О. В. Староверов, В. Б. Турундаевский. – М. : Высш. шк., 1999. 400 с.
8.Колемаев В. А. Теория вероятностей и математическая статистика / В. А. Колемаев, В. Н. Калинина. – М. : ИНФРА-М, 2009. 384 с.
9.Кремер Н. Ш. Теория вероятностей и математическая статистика : учеб. для вузов /
Н. Ш. Кремер. – М. : ЮНИТИ, 2010. 552 с.
10.Новорожкина Л. И. Математическая статистика с элементами теории вероятностей в задачах с решениями : учеб. пособие. – М. : МарТ», 2005. 608 с.
11.Фадеева Л. Н.Сборник задач по теории вероятностей и математической статистике : метод. пособие / Л. Н. Фадеева, Е. Е. Баштова, А. В. Лебедев, А. П. Шашкин; под общ. ред. Л. Н. Фадеевой. – М. : МАКС Пресс, 2010. 364 с.
12.Тиунчик М. Ф. Случайные величины : учеб. пособие / М. Ф. Тиунчик. – Хабаровск :
ХИНХ, 1993. 116 с.
13.Тиунчик М. Ф. Руководство к решению задач по теории вероятностей и математической статистике : учеб. пособие / М.Ф. Тиунчик. – Хабаровск : РИЦ ХГАЭП,
1999. 120 с.
14.Тиунчик М. Ф. Теория вероятностей. Случайные события : учеб. пособие / М. Ф. Тиунчик. – Хабаровск : РИЦ ХГАЭП, 2000. 80 с.
15.Тиунчик М. Ф. Линейная алгебра : контрольно-измерительные материалы по дисциплине : учеб. пособие / М.Ф. Тиунчик. – Хабаровск : РИЦ ХГАЭП, 2014. 84 с.
16.Тиунчик М. Ф. Математический анализ : контрольно-измерительные материалы по дисциплине : учеб. пособие / М. Ф. Тиунчик. – Хабаровск : РИЦ ХГАЭП, 2015. 124 с.
17.Чеботарёв В. И. Теория вероятностей : учеб. пособие / В. И. Чеботарёв. – Хабаровск : ДВГУПС, 2014. 233 с.
18.Чистяков В. П. Курс теории вероятностей / В. П. Чистяков. – М. : Наука, 1987. 240 с.
90
