
5652
.pdf
(i)
sup n an (T , ) c |
|
r |
, |
(5.4) |
n |
|
|
|
|
|
|
|
|
(ii) если |
|
r |
, то |
|
|
|
lim sup n an (T , n ) c |
|
r |
. |
(5.5) |
n |
|
|
|
|
|
|
|
|
Всюду в статье неравенство A << B означает A << c ∙ B, где константа, c > 0,
абсолютная или зависит только от p,q, α. Соотношение A ≈ B понимается как
A << B << A. Обозначения := и =: используются для определения новых вели-
чин; N, Z – множества всех натуральных и целых чисел соответственно; K
означает либо конечное, либо счётное бесконечное индексное множество,
символизирует конец доказательства.
§2 Оценки an (T , ) и |
Lq (I ) на интервале I (a, b) (0, ) |
Критерий ограниченности и компактности оператора Римана – Лиувилля заключён в следующей теореме.
Теорема 5.3[32]. Пусть I = (a, b), 0 ≤ a < b ≤ ∞, α > 0,
0 < q < p < ∞, |
1 |
: |
1 |
|
1 |
, p max(1/ , 1). Тогда |
|
||||||||
|
|
|
|
|
|||||||||||
|
|
s |
q |
|
p |
|
|
|
|
|
|
||||
(i) оператор Tα, υ ограничен из Lp(I) в Lq(I), если |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
s / p |
1/ s |
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
(x)(x a) 1 |
|
qdx |
|
|
(t)(t a) 1 |
|
q dt |
|
|||
B |
b t a s / p |
|
b |
|
|
|
, |
||||||||
|
a |
|
t |
|
|
|
|
|
|
|
|
|
|
||
причём
T , |
L p (I ) |
Lq (I ) |
B. |
|
|
(ii) оператор Tα, υ : Lp(I) → Lq(I) компактен, если
51
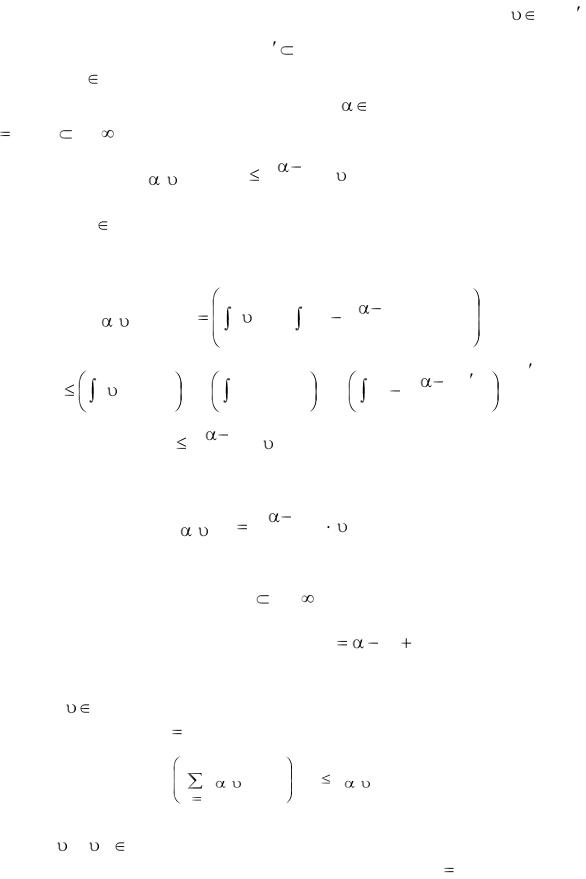
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B < ∞. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Из теоремы следует, что если Tα, υ : Lp(I) → Lq(I) ограничен, то |
Lq (I ) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
для любого внутреннего интервала I |
|
|
|
|
|
|
|
I . В частности, если Tα, υ : Lp(0, ∞) → |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Lq(0, ∞), то υ Lq(I) для любого I = (a, b) при 0 < a < b < ∞. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Лемма 5.2.1. Для 0 < q < 1 < p < ∞, |
|
N на конечном интервале |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
I (a, b) |
(0, |
) выполняется оценка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
T , |
f |
|
|
|
L |
|
(I ) |
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
1/ p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Lq (I ) |
|
|
|
f |
|
|
|
L p (I ) , |
|
(5.6) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
для всех |
f |
L p (I ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Доказательство. Применяя неравенство Гельдера с показателями p и p', получаем |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
1/ q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
x(x t) |
|
|
|
1 f (t)dt |
|
|
||||||||||||||||||||||||||||||||||||
|
|
T , |
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x) |
|
|
|
|
|
|
dx |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Lq (I ) |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
b |
|
|
|
|
|
|
|
|
|
1/ q |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1/ p |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
1/ p |
|
||||||||||||||||||||||||||||||
|
|
|
(x) |
|
q dx |
|
|
|
|
|
|
|
|
|
|
f (t) |
|
|
|
|
|
|
p dx |
|
b t |
|
( 1) p dt |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
1/ p |
|
|
|
|
|
|
|
|
|
|
|
L (I ) |
|
|
|
f |
|
|
|
L |
p |
(I ). |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
В дальнейшем величина |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
J |
, |
|
|
|
(I ) |
: |
|
I |
|
|
|
|
|
|
|
1/ p |
|
|
|
|
|
|
|
Lq (I ) |
. |
|
|
|
|
|
|
|
|
(5.7) |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
будет играть важную роль, поэтому в леммах 2.2 – 2.3 докажем ряд её
свойств на конечном интервале I (0, ) . |
|
|
|
|
|
||||||
Лемма 5.2.2. Пусть 0 < q < 1 < p < ∞, |
1 |
|
1 |
|
1 |
. |
|||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
r |
|
p |
r |
|||
|
N |
|
|
|
|
|
|
|
|
|
|
(i) Для |
Lq (I ) и Ik |
справедливо неравенство |
|||||||||
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
N |
|
1/ r |
|
|
|
|
|
|
(5.8) |
|
|
|
r |
|
|
|
|
|
|
|||
|
J |
, (I k ) |
|
|
J , |
(I ). |
|||||
|
|
|
|
|
|
||||||
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
(ii) Для 1, |
2 Lq (I ) и любого разбиения интервала Ik имеем |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
52 |
|
|
|
|
|
|
|
|
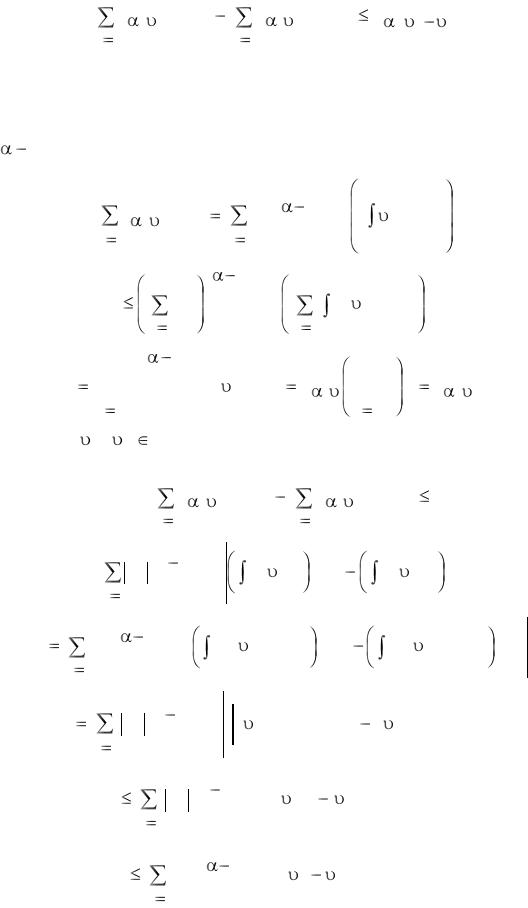
|
|
|
N |
|
|
|
1 (Ik )r |
|
|
|
N |
|
, 2 (Ik )r |
|
|
|
|
|
|
|
|
|
|
|
(I )r . |
|
|
|
|||||||
|
|
|
|
J , |
|
|
|
|
J |
|
|
J , |
|
1 |
2 |
|
(5.9) |
||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
k |
1 |
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|||
|
Доказательство. (i) Применяя неравенство Гельдера с показателями |
||||||||||||||||||||||||||||||||||
|
r |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и |
1 |
, получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
( 1/ p)r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
N |
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r / q |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
( |
|
1/ p)r |
|
|
|
|
|
|
|
|
q dx |
|
|
|
||||||||||
|
|
|
|
J , (Ik )r |
|
|
|
|
Ik |
|
|
|
|
|
(x) |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
k |
1 |
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
Ik |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
N |
( |
|
|
1/ p)r |
N |
|
|
|
|
|
|
|
|
|
|
r / q |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
qdx |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
Ik |
|
|
|
|
|
|
|
|
|
|
Ik |
|
(x) |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
k |
1 |
|
|
|
|
|
|
|
|
k |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
N |
|
( |
|
1/ p)r |
|
|
|
r |
|
|
|
|
|
|
N |
|
|
r |
J r , (I ). |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Ik |
|
|
|
|
|
|
|
|
|
|
|
|
J , |
|
Ik |
|
|
|
||||||||||||||
|
|
|
k |
1 |
|
|
|
|
|
|
|
|
|
Lq (I ) |
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
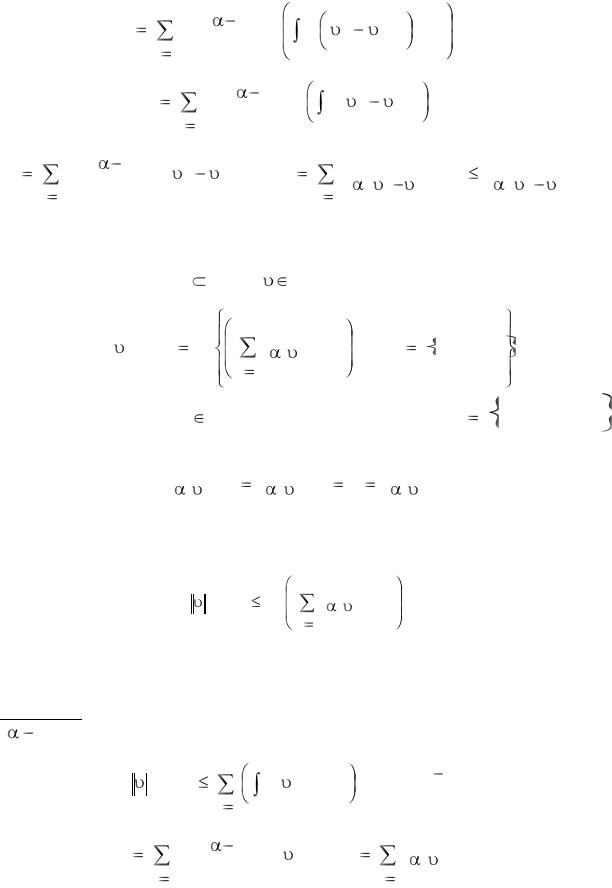
(ii) Пусть |
1, |
2 |
|
|
Lq (I ) , 0 < r < 1 и 0 < q < 1 < p < ∞, тогда |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
N |
1 (Ik )r |
|
|
N |
|
|
2 (Ik )r |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
J , |
|
|
|
J , |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
k |
1 |
|
|
|
|
|
|
|
|
k |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N Ik (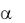 1/ p)r k 1
1/ p)r k 1
N |
( 1/ p)r |
|
|
|
|
Ik |
( |
|
|
|
|
|
Ik |
|
k 1 |
|
|
||
|
|
|
||
N Ik ( 1/ p)r k 1
1/ p)r k 1
N Ik ( 1/ k 1
1/ k 1
|
|
|
|
|
|
|
|
|
|
q |
r / q |
|
|
|
|
|
|
|
|
|
|
|
|
q r / q |
|
|
|||||||||
|
Ik |
|
|
1 |
|
|
|
|
|
|
Ik |
|
2 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
|
r )q / r r / q |
|
|
|
|
|
( |
|
|
|
2 |
|
r )q / r r / q |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ik |
|
|
|
|
|
|
|
|
||||
|
1 |
|
r |
|
Lq / r (Ik ) |
|
|
|
|
|
2 |
|
r |
|
|
Lq / r (Ik ) |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
p)r |
|
|
|
1 |
|
r |
|
|
2 |
|
r |
|
|
|
|
|
Lq / r (Ik ) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
N |
( 1/ p)r |
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Ik |
|
1 |
2 |
|
|
|
Lq / r (Ik ) |
||
k 1 |
|
|
|
|
|
|
|
|
||
53 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
N |
|
|
( |
|
|
|
|
|
1/ p)r |
|
|
|
|
|
|
|
r |
|
q / r r / q |
|
|
|
|
|
|||
|
|
|
|
|
|
|
Ik |
|
|
|
|
|
Ik |
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
N |
Ik |
|
( 1/ p)r |
|
|
|
|
|
|
2 |
|
q r / q |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
Ik |
|
1 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
N |
|
|
( |
1/ p)r |
|
|
|
|
|
|
|
|
|
r |
N |
r |
|
|
|
|
|
|
|
r |
|
|
|||||
|
Ik |
|
|
1 |
2 |
|
|
|
|
|
J |
|
|
|
|
|
|
(Ik ) J |
|
(I ). |
|||||||||||
|
|
|
|
|
|
|
|
Lq (Ik ) |
|
|
, |
|
1 2 |
|
, |
|
1 2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
k 1 |
|
|
|
|
|
|
k |
1 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Лемма 5.2.2 необходима для доказательства следующего утверждения.
Лемма 5.2.3. Пусть I |
(a, b), |
|
Lq (I ) . Тогда (i) справедливо равенство |
|||||||||||||||
|
|
|
|
|
N |
|
|
|
|
|
1/ r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
)r |
|
|
|
|
|
|
|
|
|
|
|
|
|
inf |
|
J |
, |
(I |
k |
: L |
|
I ,..., I |
N |
|
. |
(5.10) |
||
|
|
Lr (I ) |
|
L |
|
|
|
|
|
|
1 |
|
|
|
||||
|
|
|
k |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(ii) Для каждого n |
N существует разбиение |
* |
* |
, |
* |
* |
||||||||||||
L |
I1 |
I2 |
, ..., In |
|||||||||||||||
интервала I такое, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
J |
, |
(I |
*) |
J |
, |
(I *) |
... J |
, |
(I |
* ). |
|
|
|
|
||
|
|
|
1 |
|
2 |
|
|
|
n |
|
|
|
|
|||||
Доказательство. Равенство (5.10) докажем в три этапа. На первом этапе покажем, что
|
|
N |
1/ r |
|
|
|
J , (Ik )r . |
||
Lr (I ) |
inf |
|
||
L |
k |
1 |
||
|
||||
|
|
Действительно, применяя неравенство Гельдера
1 |
, получаем |
( 1/ p)r |
|
r |
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
q dx |
r / q |
|
( |
|
|
|
|
|
|
|
|
|
|
(x) |
|
Ik |
|||||||
|
Lr |
(I ) |
1 |
Ik |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
( |
1/ p)r |
|
|
|
|
|
|
|
r |
N |
|||||
|
|
|
Ik |
|
|
|
|
|
|
|
|
J |
|||||||
|
k |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Lq (Ik ) |
k |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
с показателями |
q |
и |
|
r |
|||
|
|
 1/ p)r
1/ p)r
, (Ik )r .
Вторым шагом проверим (5.10) для ступенчатых функций
54
N
(t) ck Ik (t) k 1
для некоторого разбиения I1, ... , IN интервала I и сk ≥ 0.
N |
N |
|
r / q ( 1/ p)r cr |
N |
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
J , (Ik )r |
|
Ik |
|
cr |
|
I |
|
|
|
|
|
|
|
|
|
, |
||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
k |
k |
|
|
|
|
|
|
|
|
|
|
|
Lr (I ) |
|
k 1 |
k 1 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
что в результате даёт
N |
1/ r |
|
||
|
|
|
|
|
J , (Ik )r |
|
|
Lr (I ) |
. |
|
|
|||
k 1 |
|
|
|
|
|
|
|
|
|
Далее зададим  Lq (I ) и ε > 0, выберем φ ≥ 0 так, чтобы выполнялось неравенство
Lq (I ) и ε > 0, выберем φ ≥ 0 так, чтобы выполнялось неравенство
|
|
|
|
Lq (I ) |
|
I |
|
( |
1/ p) , |
|
|
|
(5.11) |
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
которое по неравенству Гельдера влечёт |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
Lr (I ) |
. |
|
|
|
|
|
|
|
|
|
|
(5.12) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
При 0 < r < 1, используя (5.9), (5.11) и (5.12), получаем |
|
|
|
||||||||||||||||||||
N |
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|||
J , (Ik )r |
|
J , |
(Ik )r |
r |
|
|
|
|
|
|
|
|
2 r |
, |
|||||||||
|
|
|
|
|
|
||||||||||||||||||
k 1 |
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
Lr (I ) |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
что при ε → 0 доказывает (5.10). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Для проверки (ii) зафиксируем n |
|
N и определим функцию Φ на мно- |
|||||||||||||||||||||
жестве n-разбиений интервала I: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
(L) : |
max |
J |
, (Ik ) |
min |
J |
, (Ik ), |
L |
I1, ..., |
In . (5.13) |
||||||||||||||
1 |
k |
n |
1 |
|
k |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Функция Φ(L) непрерывно зависит от n-точек, определяющих разбиение
L-интервала I, следовательно, существует разбиение |
* |
* |
0 , на кото- |
L , |
Ik |
ром функция Φ достигает своего минимального значения. Покажем, что
Φ(L*) = 0. |
(5.14) |
Допустим, что существует другое разбиение L I1 , ..., In |
L* , на ко- |
тором функция (5.13) достигает минимального значения: |
|
Φmin = Φ(L`) > 0. |
|
55 |
|
Тогда найдётся номер k0 |
1, ..., n |
такой, что |
||||||
J , |
(Ik0 ) |
|
max |
J , (Ik ) |
||||
|
|
|
|
|
|
|
1 k |
n |
и |
|
|
|
|
|
|
|
|
J , |
(Ik |
0 |
) |
J , (Ik 1 ). |
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Если теперь уменьшить |
Ik 0 |
|
на достаточно малое δ, например |
|||||
|
Ik 0 |
|
|
xk 0 |
xk 0 1 |
|
xk 0 |
|
xk 0 1 |
|
, |
|
|
|||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с условием, что в полученном новом разбиении |
L |
I1 , ..., In L |
||||||||||||||
найдётся номер k1 |
1, ..., n , что |
|
|
|
|
|
|
|
|
|
|
|
||||
J , (Ik |
) |
|
max |
J |
, (Ik |
) и J , |
(Ik |
0 |
) |
J , |
(Ik |
). |
||||
1 |
|
1 k |
n |
|
|
|
|
|
|
|
|
1 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Тогда мы получили новое разбиение L’’, для которого Φ(L’) > Φ(L’’). Повторив эту процедуру, мы имеем новое разбиение L’’’:
Φ(L’) > Φ(L’’) > Φ(L’’’).
Таким образом, можно строить новые разбиения, на которых функция Φ будет принимать меньшее значение. Следовательно, всякое разбиение L’, для которого Φ(L’) > 0 не может быть минимальным, и это доказывает (5.14). В силу конструкции функции (5.13)
min |
( *) |
0 при J |
, |
(I *) J |
, |
(I |
*) ... |
J |
, |
(I |
* ), |
|
|
1 |
|
2 |
|
|
n |
||||
что и заканчивает доказательство леммы 5.2.3. |
|
|
|
|
|||||||
Пусть L Ik k K , I |
Ik – представление интервала |
I |
(0, ) в |
||||||||
|
|
k K |
|
|
|
|
|
|
|
|
|
виде объединения попарно непересекающихся конечных интервалов Ik. Рассмотрим разложение пространства Lp(I) в сумму двух подпро-
странств – Lop (I ) и Д cp (I ).
Пусть pi ( y) , j 0, 1, ... ортонормированная в L2 |
(1, 2) система поли- |
|||||
номов. Тогда для любого интервала I |
(a, b) |
(0, |
) полиномы |
|
||
p j,i (x): (b a) 1/ 2 p j |
x b |
2a |
, |
j |
0, 1, ... |
(5.15) |
b |
|
|||||
|
a |
|
|
|
||
56 |
|
|
|
|
|
|
образуют ортонормированную систему в L2 (I). Имеем
I |
|
p j, i (x) |
|
p dx (b a)1 p / 2 |
12 |
|
p j (s) |
|
p ds : c j, p |
|
I |
|
1 p / 2 , p 0. |
(5.16) |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обозначим
( f , g)Ik : Ik f (x)g(x)dx
Ik f (x)g(x)dx
скалярное произведение функций f и g, когда оно существует. Пусть
|
|
|
|
|
p j, k : |
p j, I |
k |
. |
|
|
|
|
|
|
|
|
|
|
|
Определим проектор |
c |
: L p (I ) |
c |
по формуле |
|
||||
PI |
|
L p (I ) |
|
||||||
c |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
( f , p j, k )Ik p j, k (x) Ik (x), |
|
||||
PI |
f (x) : |
|
|
|
(5.17) |
||||
|
|
j |
0 k |
K |
|
|
|
|
|
где Lcp (I ) – подпространство кусочно-полиномиальных функций:
|
|
c |
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
qk (x) I |
|
(x), qk |
|
|
|
|
1 . |
|||||||||||||||||||
|
L p (I ) L p (I , L) |
|
|
|
|
|
k |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
обозначает совокупность всех полиномов степени не превосходящей α – 1. |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Лемма 5.2.4. Если 1 ≤ p < ∞, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
Рc |
f |
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.18) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
I |
|
|
|
|
L p (I ) |
|
|
|
|
|
L p (I ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Доказательство. Из (5.17) имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F j (x). |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
PI |
|
f (x) : |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда при p > 1 имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
F j |
|
p |
|
|
|
|
|
|
|
|
|
|
|
( f , p j, k )Ik |
|
p |
Ik |
|
p j, k (x) |
|
p |
dx |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
L p (I ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
k K |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
p |
|
|
p |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
p , |
|
|
|
|
|
|
|
|
Ik |
f |
|
Ik |
p j, k |
|
|
|
Ik |
|
p j, k |
|
||||||||||||||||||||||||||
|
|
|
|
k |
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
применяя (5.16) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
c p 1c j, p |
|
|
|
|
|
f |
|
p |
|
c p 1c j, p |
|
|
|
f |
|
|
|
p |
, |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
j, p |
|
|
|
|
|
|
|
k |
K |
Ik |
|
|
|
|
|
|
|
j, p |
|
|
|
|
|
|
|
L p |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
57 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
откуда следует (5.18). При p = 1 доказательство аналогично. Определим
|
|
|
|
|
|
|
|
Po |
: |
|
|
id |
|
Pc. |
|
|
|
|
|
|
|
|
|
(5.19) |
||||||
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|||
Тогда в силу разложения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
yi |
|
|
|
|
|
p j, I , yi |
|
|
|
|
|
p j, I ( y) |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
j |
|
|
0 |
|
|
|
|
|
|
I |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
для любого i |
|
|
0 такого, что 0 ≤ i ≤ α – 1, следует |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
o |
|
|
: L p (I ) |
|
o |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
PI |
|
|
|
L p (I ), |
|
|
|
|
||||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
o |
f |
|
|
|
L p (I ) : |
|
|
|
|
y |
i |
f ( y)dy 0, j |
|
0,1..., |
1, k |
K , (5.20) |
||||||||||||||
L p (I ) : |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Ik |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
причём по лемме 5.2.4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
Рo f |
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
. |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
L p (I ) |
|
|
|
|
|
|
|
|
L p (I ) |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Если sup p f |
Ik , |
|
|
|
|
|
o |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
f L p (I ) , то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
T f (x) 0, x Ik |
|
|
|
|
|
(ak , bk ), |
|
|
||||||||||||||
потому что, при x ≥ bk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
1 |
|
|
|
|
|
|
|
|
||||
T f (x) |
(x y) |
1 f ( y)dy |
|
c j x |
1 j |
yi f ( y)dy 0. |
||||||||||||||||||||||||
|
|
Ik |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
0 |
|
|
|
|
|
Ik |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
o |
|
выполнено дизъюнктное |
||
Отсюда следует, что в подпространстве L p (I ) |
|
|||||||||||||||||||||||||||||
свойство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
, |
f |
|
|
|
|
q |
|
|
|
|
|
|
|
T , f |
|
q |
|
, f |
o |
(5.21) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
Lq (I ) |
|
|
|
|
|
|
|
|
Lq (Ik ) |
L p (I ). |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
k K |
|
|
|
|
|
|
|
|
||||||||||||
Таким образом, формулы (5.17) и (5.19) задают ограниченные операторы |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
: L p (I ) |
|
c |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
PI |
|
|
|
L p (I ), |
|
|
|
|
||||||||||||
PIo : Lp (I ) Lop (I )
такие, что их сумма
58

|
Po |
Pc |
id |
(5.22) |
|
I |
I |
|
|
является тождественным оператором. В силу |
(5.21) оператор T , |
|||
дизъюнктен на |
o |
|
|
|
L p (I ) , а также заметим, что |
|
|||
rank PIc 
 card K.
card K.
Из разложения (5.22) следует, что
|
|
|
|
|
|
|
o |
|
c |
|
o |
|
|
|
c |
|
|
|
(5.23) |
||
|
|
T |
, |
|
|
T |
, PI |
T |
, PI |
|
:T |
, |
|
|
T |
, . |
|
||||
Следующая лемма уточняет значение нормы оператора T , |
при его |
||||||||||||||||||||
|
|
|
|
|
|
|
o |
(I ) |
и играет ключевую роль в получении |
||||||||||||
сужении на подпространство L p |
|||||||||||||||||||||
дальнейших оценок. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Лемма 5.2.5. |
Пусть 0 < q < 1 < p < ∞, |
I |
(0, |
|
), L |
Ik k 1, |
|||||||||||||||
I Ik и |
Lq (Ik ) . Тогда для любой функции |
f |
o |
(I , L) |
|
|
|||||||||||||||
L p |
|
|
|||||||||||||||||||
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
, |
f |
|
L |
(I ) |
J |
, |
(Ik ) |
r /(1 |
r) |
|
r |
|
f |
|
L p (I ) |
. |
(5.24) |
||
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
q |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство. Используя лемму 5.2.1 и неравенство Гельдера с пока-
зателями |
p |
и |
|
r |
|
|
, мы получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
q |
|
|
r)q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
(1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
T , |
f |
|
q |
|
|
T , |
( Ik f |
|
|
|
|
q |
J |
, (Ik )q |
|
Ik f |
|
|
|
q |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
q |
|
|
|
|
|
|
q |
|
|
|
|
p |
|||||||||||||
|
|
|
|
|
|
|
k |
|
|
k |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
(1 |
|
|
|
|
r)q |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
qr |
r |
|
|
|
|
q p / q q / p |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
J , |
|
(Ik ) (1 |
r)q |
|
|
Ik f |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
K |
p |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
59

|
|
|
|
|
|
|
|
|
|
|
|
|
(1 |
|
r)q |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
J , |
(Ik ) (1 |
r) |
|
|
|
|
|
|
|
f |
|
|
|
q |
. |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Лемма 5.2.6. |
Пусть 0 < q < 1 < p < ∞, I |
|
|
|
|
|
(0, |
), |
L Ik k K , |
||||||||||||||||||||||
I Ik , P |
o |
: L p (I ) |
|
o |
|
|
|
Lq (Ik ) для любого k. Зададим по- |
|||||||||||||||||||||||
|
|
L p (I , L) и |
|
||||||||||||||||||||||||||||
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
следовательность натуральных чисел |
nk |
|
таких, что |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
n |
(nk |
1) |
|
|
1 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
(5.25) |
|||||
|
|
|
|
|
|
k |
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|||
a |
1) |
1 |
(T |
, |
Po ) |
2 |
|
n |
1 |
|
|
r J |
, |
|
|
(I |
k |
)1 |
r |
. (5.26) |
|||||||||||
(n |
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
k |
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Доказательство. Заметим, что в силу формулы (5.25) лишь конечное число nk может быть отлично от единицы. Для таких nk > 1, используя лемму 5.2.3, мы разобьём соответствующие интервалы Ik ещё на nk интер-
валов Ik*,1, ..., Ik*, nk с условием, что
J , (Ik*,1) ... J , (Ik*, nk ).
Если же nk = 1, то положим Ik*,1 : Ik . В результате мы построили новое разбиение интервала I
* |
* |
L |
Ik, j :1 j nk , k K . |
Причём по формуле (5.8)
J |
, |
(I |
* |
j |
) n 1/ r J |
, |
(I |
k |
), 1 |
j n . |
(5.27) |
|
|
k, |
k |
|
|
k |
|
||||
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим проекции относительно нового разбиения
P |
c |
: L p (I ) |
c |
* |
o |
: L p (I ) |
o |
* |
|
L p (I , L ) и P |
|
L p (I , L ) . |
|||||
* |
|
|
* |
|
|
|
||
|
|
|
|
60 |
|
|
|
|
