5601

дата подряд не подошли).

Ответ: вероятности составляют соответственно 0,444, 0,278, 0,159 и 0,881.

Пример 7. Преподаватель принимает экзамен и ставит 3 при первом же верном ответе, но теряет терпение после 4 неверных ответов. Студент знает 10% вопросов. Каковы шансы для него сдать экзамен? Сдать его после 3-го вопроса?

Решение. Судя по условию, шансы правильно ответить на вопрос постоянны и равны р 0,1 (это возможно, если вопросов много и можно пренебречь уменьшением выбора). Тогда риск ответить неверно составляет 1 0,1 0,9. Экзамен не будет сдан лишь в том случае, если студент неверно ответит на 4 вопроса подряд. Обозначим события А ‒ экзамен сдан; А ‒ экзамен не сдан, А3 ‒ экзамен сдан после 3-го вопроса. Находим

раз из 4 ответить правильно и тем самым сдать экзамен. Вероятность сдать экзамен именно после 3-го вопроса:

Р А3 1 р 1 р р 0,9 0,9 0,1 0,081.

Полезно подумать, почему вероятнее всего сдать экзамен после 1-го вопроса, но студенту выгодно, чтобы преподаватель задал как можно больше вопросов.

§ 3. Полная вероятность. Формула Байеса

Иногда вероятность события зависит от дополнительных условий, например, событий, произошедших раньше. В этом случае надо учесть как вероятности выполнения таких условий (называемых гипотезами), так и вероятность самого события при разных условиях.

Формула полной вероятности. Если для наступления события А необходимо наступление одной из гипотез H1 , H 2 , , Hn , то вероятность самого события А

Пример 1. В группе из 20 студентов 4 отличника, готовых к занятиям в 90% случаев. Остальные 16 готовы к 60% занятий. Новый преподаватель, незнакомый с группой, вызвал кого-то. Каковы шансы, что студент ответит?

Решение. Мы не знаем, кого вызвал преподаватель: отличника или нет, а от этого зависит вероятность события А ‒ «студент готов к занятию». Выдвинем 2 гипотезы: H1 ‒ «вызвали отличника»; H2 ‒ «вызвали обычного студента».

Студента вызывают случайным образом, и можно применить классическое определение: вероятность вызвать отличника равна доле отличников в составе

Теперь вероятность каждой гипотезы умножим на вероятность интересующего нас события при данной гипотезе, и всё сложим:

Ответ: с вероятностью 0,66 студент окажется готов к занятию.

Пример 2. Рекламу слышат 40% населения, после чего 30% услышавших рекламу обращаются в фирму. Среди не слышавших рекламу в фирму обращаются 2%. Каковы шансы, что случайный прохожий обратится в фирму?

Решение. Обозначим событие А ‒ «прохожий обратится в фирму», гипотезы

Ответ: случайный прохожий обратится в фирму с вероятностью 0,132.

Если интереснее не событие, а гипотеза, ему предшествовавшая, помогает Формула Байеса. Вероятность гипотезы ‒ это доля соответствующего слага-

емого в общей сумме при вычислении полной вероятности:

где P Aнайдено по формуле полной вероятности.

12

Пример 3. На складе хранятся 6 изделий завода А, 14 изделий завода Б, 30 изделий завода В. Завод А выпускает примерно 0,5% брака, заводы Б и В ‒ соответственно 0,3% и 0,1%. Взятое изделие оказалось бракованным. Какова вероятность, что в этом вина завода В?

Решение. С одной стороны, большинство изделий поступает с завода В. Но он выпускает меньше всех брака. Поэтому вопрос о виновнике не так очевиден.

Учтём, что всего на складе хранятся 6 14 30 50 изделий, и запишем все 6 необходимых вероятностей, переведя проценты в десятичные дроби:

Находим вероятность брака для случайно взятого изделия:

Можно заметить, что наиболее вероятный виновник ‒ завод Б, его доля в формировании всей вероятности наиболее велика.

Ответ: вероятность вины завода В – 0,294 (29,4%). Подумайте, как можно было упростить вычисления.

§ 4. Схема независимых испытаний. Формула Бернулли

Если в отдельном испытании некоторое событие происходит с вероятностью р , то вероятность того, что в серии из n испытаний событие наступит в точности k раз, составляет, согласно формуле Бернулли,

где Cnk ‒ число сочетаний (§ 1). Независимость испытаний означает, что вероят-

ность события не меняется и в каждом отдельном испытании равна р .

Пример 1. Замечено, что мастерская выполняет в срок 80% заказов. Поступили 4 заказа. Какова вероятность, что из них в срок будут выполнены

п4 ‒ число поступивших заказов. Параметр k меняется:

13

Нет никаких указаний, что выполнение заказа как-то зависит от выполнения остальных. Применяем формулу Бернулли:

Соответственно 1 0,974 0,026 , т.е. менее 3% ‒ риск, что будет выполнено менее 2 заказов (1 или ни одного).

Ответ: в точности 2 заказа будут выполнены с вероятностью 0,154; в точности 3 заказа ‒ с вероятностью 0,41; хотя бы 2 ‒ с вероятностью 0,974.

Пример 2. В среднем 1 час из 8 рабочий вынужден простаивать. Что вероятнее: что из 5 интересующих нас рабочих в данный момент работают все, или что хотя бы один отдыхает?

Решение. Для отдельно взятого рабочего вероятность простоя в любой фиксированный момент времени неизменна: р 1/ 8 0,125 . Каждый из 5 рабочих ‒ это испытание, а событие ‒ «отдельно взятый рабочий сейчас отдыхает». Итак,

Шансы, что все работают и никто не простаивает, составляют 0,513 и превышают 50%. Значит, вероятность, что хотя бы кто-то простаивает, меньше поло-

вины и равна 1 0,513 0,487 .

Ответ: вероятность, что все работают, равна 0,513. Вероятность, что кто-то простаивает, равна 0,487. Немного вероятнее, что все работают.

Замечание. Когда надо найти и сложить несколько вероятностей, нередко выгоднее найти вероятность противоположного события и вычесть её из 1. Так, если в примере 2 понадобится вероятность того, что отдыхают не менее 2 чело-

§ 5. Предельные теоремы в схеме независимых испытаний

Формула Бернулли справедлива при любой вероятности события, но неудобна, хотя и верна, при большом числе испытаний. В этом случае помогают предельные теоремы (формулы) Пуассона и Лапласа.

Значения функции f a e a даны в приложении А. Формулой удобно пользоваться, если a 9 . При a 9 применяется

Локальная формула Лапласа. Если число испытаний п , то вероятность того, что в n испытаниях событие наступит ровно k раз, составляет

даны в приложении Б.

Пример 1. При перевозке портится 0,01% изделий. Каковы шансы, что при перевозке 20 тыс. изделий испортится не более двух? Каков риск, что испортится более 3 изделий?

Решение. Событие ‒ поломка отдельного изделия, вероятность такого собы-

Ответ: не более 2 изделий испортится с вероятностью 0,675. Более 3 изделий испортится с вероятностью 0,145.

Пример 2. Четверть клиентов банка продлевает вклад на новый срок. Какова вероятность, что из 200 интересующих нас клиентов, действующих независимо, вклад продлят в точности 50 человек? В точности 60?

Решение. Каждый из 200 клиентов ‒ отдельное испытание, п 200 . Вероятность продления вклада р 0,25 . Величина пр 200 0,25 50 намного больше 9,

искать е 50 5050 по формуле Пуассона невозможно. Применим формулу Лапласа:

50!

Ответ: вероятность, что 50 клиентов из 200 продлят вклад ‒ около 0,065. Вероятность, что так сделают ровно 60 клиентов ‒ около 0,017.

В такой постановке задача не имеет практической ценности: не произойдёт ничего особенного, если вклад продлят не 50, а 51 или 49 человек. Важнее, продлят ли вклад «не менее 50», «не более 100», «от 50 до 100» клиентов и т.п. Перебор всех подходящих значений в таких случаях громоздок, и помогает

Интегральная формула Лапласа. Если число испытаний п 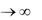и вероят-

ность события в отдельном испытании постоянна и равна р, то вероятность того,

Лапласа. Для её вычисления применяют таблицы (приложение В).

16

Пример 4. Примерно половина студентов выполняет контрольную работу с 1-го раза. Каковы шансы, что в потоке из 40 студентов с 1-го раза напишут работу более 24 человек? Хотя бы 18?

Решение. Фраза «половина студентов» означает, что для отдельно взятого студента шанс выполнить работу р 0,5 . Численность потока ‒ это число испытаний: п 40 . Очевидно, число выполненных работ не превышает 40.

а) в 1-м случае работу должны выполнить более 24, т.е. хотя бы 25 человек.

Замечание. Иногда вопрос ставится так: «какова вероятность, что работу выполнит более 70% студентов» (и т. п.). Чтобы получить границы k1 или k2 , надо перевести проценты в числа (например, 70% от 90 – это 0,790 63 человека).

§ 6. Дискретные случайные величины

Во многих задачах случайное событие можно выразить числом: выигрыш в лотерее, прибыль предприятия и т.д. Такие числа называют случайными величинами (СВ). Дискретные СВ (ДСВ) принимают значения из некоторого набора, непрерывные СВ (НСВ) ‒ из интервала. Так, выручка магазина ‒ непрерывная СВ, а число посетителей за минуту ‒ дискретная.

Закон распределения ДСВ ‒ таблица, где даны возможные значения величины и вероятности, с которыми она принимает указанные значения.

17

Функция распределения СВ ‒ это вероятность того, что величина примет значение, меньшее указанного: F x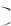 P CB x .

Случайные величины обычно обозначают буквами, указывая их смысл, например, Х – «прибыль фирмы за год». Всегда малая буква ‒ обозначение числа, большая буква ‒ обозначение некоторого понятия.

Пример 1. В лотерее выпущено 200 билетов, на 1 из них падает выигрыш в 500 руб., на 4 билета ‒ выигрыш в 50 руб., на 20 билетов ‒ выигрыш в 5 руб. Величина Х ‒ выигрыш по купленному билету. Составим закон распределения Х.

Решение. Величина Х может принять одно из значений: 500 руб., 50 руб., 5 руб., а также 0 руб., если билет ничего не выиграл.

Вероятность того, что билет выиграл 500 руб. ‒ это отношение числа билетов

175

не выигрывают ничего и потому P X 0 0,875 .

200

Ответ: закон распределения выигрыша по случайно купленному билету

Обратите внимание, что сумма всех вероятностей всегда равна 1.

Зная закон распределения, можно найти числовые характеристики ‒ матема-

Замечание. Если случайную величину вместо буквы Х обозначить другой буквой, например, как Y, получим обозначения MY , DY , M Y 2 , P a Y b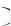 и т.д.

Записи P X a; b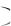, P CB a; b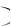, P a X b , P a CB b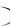равноправны.

18

Пример 2. Для случайной величины из примера 1 найдём её числовые характеристики и поясним результаты. Перепишем закон распределения:

Дисперсию найдём обоими способами, чтобы проверить, совпадут ли ответы:

Итак, при покупке большого числа билетов средний выигрыш составит 4 руб. (без учёта затрат на билет!). Но в среднем выигрыш будет отличаться от ожидаемых 4 руб. на 35,87 руб.

Ответ: MX 4 руб., DX 1286,5 руб.2 , 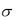Х 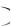35,87 руб.

Замечание. В основном выигрыш отличается от ожидаемого не на 35 с лишним рублей, а на 4, поскольку почти все выигрыши равны 0. Большое среднее отклонение получено из-за выигрыша в 500 руб., пусть даже очень редкого. Дисперсия чувствительна к выбросам – значениям, сильно отличающимся от остальных. Каким способом лучше считать дисперсию, зависит от задачи.

При составлении закона распределения можно применять любые известные формулы: Бернулли, классическое определение вероятности и т.д.

Пример 3. Примерно 40% фирм работают менее 4 лет. Нас интересуют 3 фирмы, начавшие работу. Величина Y ‒ число фирм среди них, которые проработают менее 4 лет. Составим закон распределения величины Y и найдём её числовые характеристики.

Решение. Из условия получаем, что p 0,4 ‒ вероятность, что отдельная фирма проработает менее 4 лет. Обозначим n 3 ‒ общее число фирм. Величина Y принимает 4 возможных значения: Y 0 (все фирмы продолжат работу), Y 3 (все фирмы прекратят работу), а также Y 1 и Y 2 (соответственно 1 или 2 фирмы прекратят работу).

Судя по условию, фирмы работают независимо, и имеет место схема независимых испытаний. Поэтому для вычисления вероятностей применим формулу Бернулли (о вычислении Cnk см. § 1).

19

Смысл результатов в следующем:

а) если все возможные фирмы поделить на тройки, то в среднем 1,2 фирмы в

Пример 4. Для данных примера 3 составить функцию распределения и найти значения F 0 , F 0,5 , F 2,5 , F 6 .

Решение. Для ДСВ функция распределения меняется скачком в точках, равных возможным значениям. Величина скачка равна вероятности значения:

Интересующие нас значения функции:

равно 0, а вероятность этого составляет 0,216;

20