УДК 519.95

ББК В 1

Б 94

Бушин П. Я. Методы оптимальных решений : практикум по выполнению лабораторных работ / П. Я. Бушин. – Хабаровск : РИЦ ХГАЭП, 2015. – 92 с.

Содержание практикума в основном соответствует требованиям государственных образовательных стандартов высшего профессионального образования по направлению подготовки «Менеджмент» и «Экономика» квалификации (степень) «бакалавр» очной и заочной форм обучения и программе дисциплин «Методы оптимальных решений» и «Математические методы в управлении».

В практикуме приводятся краткие теоретические сведения по рассматриваемым темам, решаются задачи с конкретной информацией, анализируются результаты решения с рекомендациями по принятию решений на основе этого анализа.

Все расчёты проводятся с использованием компьютерных программ. Приводятся рекомендации по их применению и вводу исходной информации, а также указываются возможные окна отчётов, необходимые для выполнения лабораторных работ.

Практикум предназначено для обучающихся по направлению «Менеджмент и Экономика» по очной и заочной форм обучения, кроме того, он может быть использован и магистрантами разных направлений обучения и специалистами, принимающими участие в выработке управленческих решений на основе методов оптимальных решений.

Рецензенты:

Р. В. Намм, доктор физ.-мат. наук, профессор, гл. научный сотрудник ВЦ ДВО РАН

В. А. Кузнецов, канд. физ.-мат. наук, доцент кафедры ММиИТ ДВИ-филиал РАНХиГС

Утверждено издательско-библиотечным советом академии в качестве учебного пособия

Бушин П. Я., 2015 Хабаровская государственная академия экономики и права, 2015

2

ВВЕДЕНИЕ

Современному экономисту и менеджеру для принятия решений в своей профессиональной деятельности необходимо владеть методами количественного моделирования анализируемых процессов для разработки альтернатив эффективного развития и управления этими процессами.

В предлагаемом практикуме основное внимание уделено вопросам математического моделирования на основе балансовых и оптимизационных моделях. К ним относятся модели межотраслевых связей, модели на основе линейного программирования, сетевое моделирование, теория игр, теория массового обслуживания, оптимальное управление запасами и др.

Для построения математической модели необходимо иметь чёткое представление о цели функционирования исследуемой системы и располагать информацией об ограничениях, которые определяют область допустимых значений управляемых переменных. Анализ модели должен привести к определению наилучшего управляющего воздействия на объект управления при выполнении всех установленных ограничений.

Выполнение лабораторных работ, предлагаемых в практикуме, должно дать студентам достаточное первоначальное представление о математическом аппарате разработки методов принятия решений, а также показать сферы приложений этих методов на наглядных примерах.

3

1. Лабораторная работа № 1

Анализ межотраслевых связей Краткие теоретические сведения

Система балансов как экономико-математическая модель является незаменимым рабочим инструментом государственного регулирования экономики.

Обычно составляются отчётные и плановые балансы. Отчётные балансы строятся на основе отчётных статистических данных, и их анализ помогает правильно оценить сложившиеся пропорции в экономике страны и сформулировать основные задачи на следующий период.

Плановые балансы позволяют выработать рекомендации по сбалансированности всех элементов общественного производства в будущем периоде и установить соответствие потребностей и ресурсов хозяйственной системы, которые сложатся в экономике в случае выполнения рекомендаций.

Анализ плановых балансов позволяет определить возможные темпы и пропорции развития экономики и установить, в какой степени тот или иной вариант расчётов соответствует социально-экономическим задачам планового периода, в какой мере в нём учтены требования объективных экономических законов.

1.1. Схема и модель межотраслевого баланса производства и распределения продукции

Введём необходимые для дальнейшего понятия.

Промежуточный продукт (промежуточный спрос) – это часть валового продукта (спроса), представляющего собой закупки i-го вида продукции j-ми отраслями в качестве исходных материалов, т.е. это продукт, который поступает из i-й отрасли в j-ю для дальнейшей переработки в текущем периоде. Будем обозначать его через xij.

Конечный продукт (конечный спрос) – это часть общего спроса,

представляющая закупки продуктов, выходящих из сферы производства в область конечного использования на потребление и инвестиции. Будем обозначать его через yi.

Условно-чистая продукция или добавленная стоимость – это созданная стоимость, состоящая из заработной платы, предпринимательского дохода, различного вида налогов и амортизации. Условно-чистая продукция – это стоимостный эквивалент конечной продукции. Будем обозначать его через zj.

4

МОБ представляет собой экономико-математическую модель процесса воспроизводства, которая в развёрнутом виде отражает взаимосвязи по производству, распределению, потреблению и накоплению каждого вида продукции в единстве материально-вещественного и стоимостного аспектов воспроизводства. Он состоит из двух таблиц, наложенных одна на другую. В первой из них в отраслевом разрезе представлена структура затрат, или структура используемых ресурсов, необходимых для каждой отрасли. В том числе и элементы условно-чистой продукции (добавленной стоимости). Во второй – распределение выпуска каждого вида продукции на нужды промежуточного (текущего производственного) и конечного использования. Затраты отражены по столбцам общей таблицы, а распределение – по строкам.

Пересекающаяся часть этих двух таблиц образует так называемую “шахматку”, или первый квадрант общей схемы МОБ. Строки и столбцы “шахматки”, имеющие одинаковые номера, характеризуют процесс производства (по столбцам) и распределения (по строкам) продукции одной и той же отрасли на нужды текущего производственного потребления. В пределах “шахматки” (I квадранта МОБ) отражается внутрипроизводственный оборот (промежуточные затраты – промежуточный выпуск) предметов труда и услуг.

Рассмотрим общую схему МОБ, которая в стоимостном исчислении состоит из четырёх разделов (квадрантов) (таблица 1.1).

В I и II квадрантах отражаются важнейшие материально-вещественные взаимосвязи и пропорции национальной экономики, выраженные в стоимостных измерителях – отраслевая и материально-вещественная структура фондов текущего производственного потребления и конечной продукции.

где xi – валовой продукт i-й отрасли;

n– число отраслей.

ВI и III квадрантах находят отражение важнейшие стоимостные пропорции по производству национального продукта. Здесь отражена стоимостная отраслевая структура затрат или структура используемых ресурсов, необходимых для каждой отрасли.

Каждый столбец здесь характеризуется следующим балансом:

Расходы отрасли = Промежуточные затраты + добавленная стоимость,

что в математической записи выглядит так:

Итоги одноимённых строк и столбцов таблицы МОБ равны, т.е. равны выпуск и расходы отрасли:

а, следовательно, общая сумма конечного спроса равна общей сумме добавленной стоимости:

Равенство (1.1) называется системой уравнений распределения продукции, равенство (1.2) – системой уравнений производства продукции, а (1.3) – основное балансовое соотношение.

Будем считать, что объёмы промежуточного производственного потребления прямо пропорциональны объёмам производства продукции потребляющих отраслей:

где коэффициентами пропорциональности aij являются коэффициенты прямых материальных затрат, определяемые из соотношений:

Из (1.4) следует и смысл этих коэффициентов; они показывают объём материальных ресурсов i-го вида, необходимый для производства единицы валового продукта j-го вида. После подстановки (1.4) в (1.1) получаем

Это и есть система уравнений модели В. Леонтьева “затраты-выпуск”, называемая статической моделью МОБ. Рассчитаем равновесный выпуск, найдя решение xi (i = 1, n ) системы линейных уравнений (1.6) при фиксированных

значениях спроса на конечную продукцию yi (i = 1, n ). Запишем систему уравнений (2.6) в матричной форме:

(1.6а) называется моделью затраты-выпуск В Леонтьева.

1.2. Расчёт равновесного выпуска и равновесных цен

Решим уравнение (1.6а) относительно Х, определив равновесный валовый выпуск отраслей, обеспечивающий заданный уровень спроса Y на конечную продукцию:

называется обратной матрицей Леонтьева или матричным мультипликатором, (мультипликатором Леонтьева). Её элементы bij показывают потребность в валовом выпуске продукции i-й отрасли для производства единицы конечной продукции j-й отрасли и называются коэффициентами полных материальных затрат. Таким образом, В – это мультипликатор, показывающий эффект распространения спроса на валовую продукцию, первоначальным источником

7

которого является спрос на конечную продукцию. Перепишем (1,7) с учётом

(1,8) в виде

Говорят, что решение системы уравнений МОБ позволяет определить равновесный выпуск, имея в виду под общим равновесием соотношение в экономической системе, которое характеризуется равновесием спроса и предложения всех её элементов.

Определим равновесные цены, воспользовавшись системой уравнений производства продукции. Равновесные цены позволяют исследовать эффект распространения изменения цены, вызванный изменением элементов добавленной стоимости и построить ценовую модель МОБ.

Обозначим через vj = zj / xj величину добавленной стоимости, приходящейся на единицу валовой продукции отрасли и называемой долей добавленной стоимости. Тогда, учитывая, что zj = vj xj, (1.2) перепишем в виде:

возмещение стоимости, а vj – вновь созданную стоимость (с учётом амортизации и налогов). Система равенств (1.11) представляет собой модель балансовых цен, на основе которой можно выяснить, как через посредство структуры потребляемых каждой отраслью ресурсов изменяется структура цен при варьировании величины добавленной стоимости.

Если для расчётного периода доля добавленной стоимости будет равна vj, то цены Pj (j = 1, n ) будут определяться по (1.11) из соотношений

i1

Вматричном виде эту систему можно переписать как

1.3. Балансы трудовых ресурсов и основных производственных фондов

Обозначим через L общую потребность в трудовых ресурсах, необходимых для выпуска продукции в объёмах , (j = 1,2,…,n). Тогда

объёмы затрат труда в j-й отрасли).

Кроме того, дополним схему МОБ производства и распределения продукции балансом основных фондов

во всех отраслях национальной экономики для производства единицы конечного продукта в k-й отрасли. Соотношения (1.17) и (1.18) показывают, что прямые затраты ресурса на выпуск валовой продукции совпадают с их полными затратами на выпуск конечного продукта.

Рассмотрим постановку задачи и последовательность её решения для выполнения лабораторной работы по обсуждаемой теме на конкретном примере.

1.4. Постановка задачи

Цель – научиться использовать экономико-математическую модель межотраслевых связей в анализе межотраслевых пропорций на основе коэффициентов прямых затрат и эффектов мультипликаторов.

Задача. Дан следующий отчётный межотраслевой баланс (МОБ) (пример условный).

В шахматке указаны межотраслевые потоки промежуточной продукции, в последних двух строках за пределами таблицы – объёмы затрат труда и фондов, а в последнем столбце – конечная продукция. Будем считать, что номенклатура отраслей следующая:

1.Сельское, лесное и рыбное хозяйство.

2.Тяжёлая промышленность.

3.Лёгкая промышленность.

4.Строительство и энергетика.

5.Транспорт и связь

6.Услуги.

10

1.5. Задания для выполнения лабораторной работы №1

1.Построить таблицу отчётного МОБ, проверить основное балансовое соотношение.

2.Составить плановый МОБ при условии увеличения спроса на конечный продукт по отраслям на 5, 4, 6, 7, 3 и 8 %.

3.Рассчитать коэффициенты прямых и полных затрат труда и фондов и проверить в плановом балансе выполнение равенств (1.17) и (1.18), используя формулы (1.15) и (1.16).

4.Определить, на сколько процентов необходимо увеличить производительность труда по отраслям для выпуска планового валового продукта с той же численностью, что и в отчётном периоде.

5.Проследить эффект матричного мультипликатора при дополнительном увеличении конечного продукта по лёгкой промышленности на 5 %.

6.Рассчитать равновесные цены при увеличении зарплаты по всем отраслям на 10% (считать доли заработной платы в добавленной стоимости по отраслям следующими: 0,33, 0,5, 0,52, 0,35, 0,43, 0,6). Проследить эффект ценового мультипликатора при дополнительном увеличении зарплаты в сельском хозяйстве на 5%.

1.6. Ход выполнения работы

Предполагается, что работа будет выполняться с помощью программы обработки электронных таблиц Microsoft Excel.

1. Заполним таблицу отчётного баланса.

При составлении этой таблицы в Excel автоматически проверяется основное балансовое соотношение, суть которого состоит в равенстве суммарного конечного продукта (последняя ячейка столбца «Кон. продукт») и суммарной добавленной стоимости (последняя ячейка строки «Доб. ст-ть») в таблице 1.2 (2 482,54 = 2 482,54). При заполнении столбца и строки «итого» необходимо воспользоваться функцией суммирования, а в остальных случаях воспользоваться возможностью вычислений в ячейках с помощью формул и копировании формул в другие ячейки.

Для составления таблицы планового баланса необходимо рассчитать плановый валовой выпуск по формуле (1.9) и плановые межотраслевые потоки по формуле (1.4), а дальше – как в отчётном балансе.

Рассчитаем сначала коэффициенты прямых материальных затрат по формуле (1.5), используя информацию отчётного баланса. Поскольку элементы столбца межотраслевых потоков делятся на валовой выпуск потребляющей отрасли, записывая формулу (1.9) в соответствующей ячейке, воспользуемся абсолютной ссылкой для номера столбца. Тогда формула для вычисления, например, а11 будет иметь вид «=В4/В$12», если х11 находится в ячейке В4, а х1 – в ячейке В12. Относительная ссылка превращается в абсолютную нажатием клавиши ”F4” в режиме редактирования. В нашем случае эту клавишу надо нажать дважды, чтобы абсолютной осталась только вторая ссылка. Вычислив а11, скопируем эту формулу на весь столбец матрицы А, а затем этот столбец – на все столбцы матрицы. Получим следующую матрицу коэффициентов прямых материальных затрат:

Рассчитаем матрицу В по формуле (1.8), для чего сначала вычислим матрицу (Е–А), а затем найдём к ней обратную. На свободном месте листа Excel введём единичную матрицу Е размерности 6х6. Для расчёта матрицы (Е–А) введём формулу в свободную ячейку для вычисления элементов этой матрицы и скопируем её сначала по столбцу вниз, а потом – столбцы вправо.

12

Рассчитаем теперь матрицу В = (Е – А) –1, используя функцию Excel вычисления обратных матриц. Для этого поместим курсор в начало массива, отведённого для матрицы В, щёлкнем на кнопке мастера функций fx, выберем категорию “математические”, а затем функцию «МОБР», щёлкнув по ней кнопкой мыши. Появится диалоговое окно работы с этой функцией. В поле «массив» необходимо указать адрес массива с матрицей (Е–А), для чего можно щелкнуть по «флажку» в конце этого поля, окно ввода при этом свернётся до строки поля, под строкой формул. В правой части этой строки будет виден тот же «флажок». После этого необходимо выделить курсором мыши массив с матрицей (Е–А) (при этом выделенный массив будет обведён мерцающим курсивом, а в начале строки появится адрес выделенного массива) и повторно щёлкнуть по этому же «флажку». При этом окно ввода приобретёт первоначальный вид. Щёлкнув по кнопке «ОК», завершим указание массива обращаемой матрицы. После этого необходимо выделить чёрным цветом место под массив, отведённый для обратной матрицы, затем щёлкнуть кнопкой мыши по строке формул (при этом адрес массива выделится синим цветом) и ввести формулу обращения матриц как формулу массива, нажав последовательно, не отпуская три клавиши “Ctrl” + “Shift” + “Enter”. Получим матрицу В:

Для расчёта планового валового выпуска по формуле (1.9) необходимо вычислить плановый конечный продукт, увеличив отчётный конечный продукт по каждой отрасли на 5, 4, 6, 7, 3 и 8 %. Получим

0,93

328,90

324,72

564,39

163,97

1266,2

Рассчитывать и размещать его лучше сразу в таблицу для планового баланса при помощи копирования формулы во все его строки по столбцу «Кон. продукт». Для расчёта по формуле (1.9) воспользуемся функцией умножения матриц «МУМНОЖ» из мастера функций, выбрав категорию «математические». Эта функция имеет два поля ввода для указания перемножаемых массивов, как это указано на рисунке 1.1.

13

Рисунок 1.1 – Диалоговое окно МУМНОЖ

Щелчком по флажку поля «Массив 1» окно ввода сверните до строки массива, затем выделите массив с матрицей В, снова щёлкните по флажку и окно ввода развернётся до первоначального вида. После этого щёлкните по флажку «Массив 2» и аналогично предыдущему выделите массив столбца «Кон. продукт». Повторным щелчком по этому флажку окно ввода разверните до первоначального вида. А затем аналогично предыдущему: щёлкните по кнопке «ОК», выделите формулу, выделите место под массив вычисленного валового продукта и нажмите последовательность клавиш “Ctrl” + “Shift” + “Enter”. Получите

171,61

820,88

1468,36

947,84

452,26

2012,74

Этот результат можно разместить сразу в столбце «Вал. продукт» таблицы планового баланса.

Для заполнения «шахматки» этой таблицы воспользуемся формулой (1.4). Для облегчения её использования разместим показатели валового продукта в последней строке таблицы и при записи формулы воспользуемся правилом организации фиксированной ссылки по второму адресу. Например, при вычислении х11 формула примет вид: «=C15*B$53», если а11 находится в клетке С15, а Х1 в клетке Б53. Как и в случае вычисления элементов матрицы А, фиксированная ссылка по второму адресу получается двойным нажатием клавиши «F4» после щелчка по клетке с адресом «Б53». После вычисления по этой формуле необходимо скопировать её сначала по столбцу таблицы, а затем столбец – по строкам. После соответствующих вычислений получим таблицу

1.3.

14

Таблица 1.3 – Таблица планового МОБ

трудоёмкости и фондоёмкости. Расчёты проводим по формулам: tj = Lj/Xj, fj = Фj/Xj, копируя их в соответствующие клетки. Получим

Рассчитаем коэффициенты полных затрат труда и фондов по формулам (1.19) и (1.20) соответственно, используя функцию умножения матриц, как при вычислении планового валового выпуска. При этом необходимо учитывать, что матрицы t и f – это строки и поэтому результаты вычисления так же будут строками.

Подсчитаем плановую потребность в труде и фондах, используя формулы (1.15) и (1.16), для чего эту потребность сначала рассчитаем отдельно по отраслям, а затем просуммируем. Получим

15

Первые 6 цифр – это потребность по отраслям, последняя – по всей экономике.

Воспользуемся теперь второй частью формул (1.17) и (1.18), для чего умножим матрицы коэффициентов полных затрат ресурсов на конечный продукт в плановом балансе. Получим

353,38 531,56

Что доказывает равенство прямых затрат ресурсов на производство валового выпуска и полных затрат ресурсов на производство конечного продукта.

4. Для выполнения четвёртого пункта рассчитаем производительность труда по валовому продукту в отчётном периоде и в плановом, но численность возьмём в обоих случаях из отчётного баланса, а затем сравним эти результаты.

В отчётном периоде производительность труда по валовому продукту

Разделив валовой продукт планового периода на ту же численность, получим

Как видим, производительность труда должна увеличиться. Определим, на сколько процентов. Разделив одно на другое, получим

1,0548 1,0525 1,0618 1,0668 1,0515 1,0745

Наибольшее увеличение производительности труда при этом потребуется для 6-й отрасли – «услуги», на 7,45 %.

5. Эффект матричного мультипликатора определим, пользуясь соотношением X = B Y. Y рассчитаем из условия дополнительного увеличения спроса на конечный продукт по 3-й отрасли (лёгкой промышленности) на 5 %. Итак, спрос на конечную продукции по всем отраслям, кроме 3-й, останется прежним, т. е. прирост спроса по этим отраслям будет равен нулю, а по 3-й отрасли такой

прирост будет равен (324,72*0,05 = 16,236). Окончательно получим,

Y = (0 0 16,236 0 0 0)Т,

16

Перемножив B и Y, получим

X = (0,48 2,29 26,65 2,52 1,39 4,57)Т.

Как видим, изменение спроса на валовую продукцию произошло по всем отраслям. В процентном соотношении это составит

(0,28 0,28 1,8 0,27 0,31 0,23).

6. Равновесные цены определим из соотношения P = BT V, а доли добавленной стоимости рассчитаем по формуле vj = zj / xj, изменив их затем из условия 10%-го увеличения зарплаты. Разделив добавленную стоимость по

Выделим зарплату, воспользовавшись информацией из задания в п. 6 о долях

Добавив 10 % от полученных величин к ранее рассчитанным показателям, получим требуемую величину доли добавленной стоимости для расчёта равновесных цен. Итак, V равно

0,586 0,315 0,307 0,395 0,385 0,711

Для расчёта равновесных цен по приведённой формуле необходимо протранспонировать матрицу коэффициентов полных затрат В. Воспользуемся функцией транспонирования из мастера функций, выбрав из категории «Ссылки и массивы» функцию «ТРАНСП». В появившемся окне ввода укажите массив матрицы В, предварительно установив курсор в начало массива, где будет размещена транспонированная матрица. Не забудьте, что это формула массива. Щёлкнув по кнопке «ОК», выделите массив размерности 6х6 чёрным цветом, активизируйте функцию транспонирования, щёлкнув по строке формул, и нажмите последовательно не отпуская клавиши “Ctrl” + “Shift” + “Enter”. В результате этого получите матрицу ВТ, умножив её на V, получим равновесные цены:

1,0394

1,0487

1,0518

1,0448

1,0474

1,0574

17

Не забудьте, что в соответствии с правилами умножения матриц вектор V перед умножением должен быть представлен в виде столбца. Как видим, результаты расчетов показали, что при 10%-ном росте зарплаты одновременно по всем отраслям цены на продукцию отраслей увеличились в пределах от 3,94 % до 5,74 %.

Рассчитаем теперь эффект ценового мультипликатора при дополнительном увеличении зарплаты по отрасли «сельское хозяйство» на 5 %. Расчёты будем вести по формуле P = BT V, где V определим из условия задачи.

V = (0,0095 0 0 0 0 0)Т.

Тогда

P = (0,01105 0,0025 0,00034 0,0005 0,00031 0,00029).

Как и ожидалось, наибольший прирост в цене продукции пришёлся на саму отрасль «сельское хозяйство» – на 1,1 %, а по остальным отраслям этот прирост составил доли процента. Например, по отрасли «тяжёлая промышленность» на 0,25 %. Эффект же ценового мультипликатора проявился в том, что при изменении цены только в одной отрасли произошло изменение цен во всех отраслях и это изменение можно отследить с помощью ценового мультипликатора BT.

1.7. Информация для выполнения лабораторной работы

При формировании варианта своего задания необходимо иметь в виду, что показатели межотраслевых потоков продукции в отчётном балансе, численность занятых в отраслях и объёмы основных производственных фондов одинаковы для всех вариантов и совпадают с данными в рассмотренном примере. Для разных вариантов меняется лишь вектор конечных продуктов. Для конкретных вариантов они следующие.

18

Межотраслевые потоки продукции для выполнения лабораторной работы необходимо взять из текста задания в п. 1.4 (для всех вариантов они будут одни и те же).

2. Лабораторная работа № 2

Анализ оптимального решения задачи использования ограниченных ресурсов

2.1. Краткие сведения из линейного программирования

Напомним некоторые моменты решения задачи линейного программирования (ЛП) симплексным методом.

Как известно, задача ЛП заключается в нахождении совокупности переменных x1, x2, … , xn, удовлетворяющих системе линейных ограничений:

достигает максимума.

В такой постановке задача ЛП называется стандартной. Если знак неравенства в системе ограничений заменить на знак равенства, то задача ЛП примет вид основной задачи ЛП.

Переход от стандартной задачи ЛП к основной осуществляется добавлением в левую часть каждого неравенства балансовой переменной.

Как известно, для каждой задачи ЛП можно составить двойственную задачу. Сформулируем двойственную задачу для стандартной задачи ЛП, записанную в виде (2.1 – 2.3).

Алгоритм составления двойственной задачи в этом случае следующий.

1. Число переменных двойственной задачи равно числу ограничений исходной задачи и наоборот.

19

2.Коэффициенты целевой функции исходной задачи становятся правыми частями ограничений двойственной задачи и наоборот.

3.Если исходная задача решается на максимум, то двойственная – на минимум и наоборот.

4.Столбцы коэффициентов при переменных в ограничениях исходной задачи становятся строками коэффициентов при переменных в ограничениях двойственной задачи и наоборот.

5.Знаки неравенств в ограничениях исходной и двойственной задачах противоположны.

6.Условия не отрицательности для переменных двойственной задачи сохраняются.

Следуя этим правилам, составим двойственную задачу к задаче (2.1 –2.3).

Найти совокупности переменных y1, y2, … , ym, удовлетворяющих системе

достигает минимума.

Зная решение исходной задачи, можно найти решение двойственной задачи, не решая её. Известно, что оценки балансовых переменных в оптимальном плане исходной задачи равны оптимальным значениям переменных двойственной задачи.

Сформулируем основные теоремы ЛП, необходимые для дальнейшего. Ограничения (2.1) и (2.5), а также (2.2) и (2.4) будем называть сопряжёнными. Теорема 1. Для оптимальных решений прямой и двойственной задач значения

функций берутся из оптимальных решений прямой и двойственной задач. Теорема 2. Для каждой пары сопряжённых условий в оптимальном

решении выполняются следующие соотношения; если одно из них выполняется как строгое равенство, то другое – как строгое неравенство и наоборот, т.е.

20

2.2. Экономическая интерпретация и свойства двойственных оценок

Придадим экономический смысл прямой и двойственной задачам для следующей простейшей формулировки.

Будем считать, что на предприятии производится n видов продукции и при этом используются m видов ресурсов. Пусть далее

– нормы расхода i-го вида ресурса на производство единицы j-го вида продукции;

– объём i-го вида ресурса;

– цена единицы j-го вида продукции;

– искомые объёмы выпуска продукции j-го вида.

В этих обозначениях задача (2.1) – (2.3) примет вид задачи определения объёмов выпуска продукции ( при известных нормах затрат ресурсов ( так, что расход каждого вида ресурса не превышал бы имеющегося запаса ресурса (, и при этом суммарный объём выпуска продукции (Z) должен быть максимальным.

Двойственная задача примет вид задачи определения оценок единицы каждого вида ресурса , таких, что оценка ресурса на выпуск единицы каждого вида продукции должна быть не меньше цены единицы этого продукта (, а суммарная оценка всех ресурсов (W) была бы минимальной.

При такой постановке двойственные оценки приобретают определённый смысл и свойства. Сформулируем их.

Свойство 1. Оценка как мера влияния ограничения на оптимальное значение целевой функции.

В соответствии с этим свойством, оценка каждого вида ресурса в оптимальном плане показывает, на какую величину изменится оптимальное значение целевой функции, т.е. максимальный объём суммарного выпуска продукции, если объём соответствующего ресурса изменить на единицу. При этом надо иметь в виду, что данное свойство справедливо, если изменение ресурса не приведёт к изменению его оценки.

21

Известно, что оценки обладают определённой устойчивостью по отношению к изменению объёма ресурса. Например, если изменить объём i-го ресурса на k единиц, то объём выпуска продукции изменится на величину , если это изменение ресурса не вышло за границу устойчивости двойственной оценки. В противном случае придётся последствия такого изменения определять, пересчитывая задачу заново. Границы устойчивости двойственных оценок определяются по определённому алгоритму и выдаются при решении задачи ЛП любым пакетом программ.

Свойство 2. Оценка как мера дефицитности ресурса.

Это свойство вытекает из соотношений (2.8) и (2.9). Из (2.8) следует, что если в оптимальном плане ресурс израсходован полностью (слева этого соотношения показан суммарный расход ресурса, а справа – его запас, и знак равенства указывает на то, что расход равен запасу), то оценка такого ресурса в оптимальном плане положительна. В соответствии с первым свойством, чем больше оценка ресурса, тем будет большее увеличение оптимального объёма выпуска продукции при увеличении такого ресурса на единицу. Такой ресурс будем называть дефицитным.

Дефицитность здесь понимается в ином смысле, чем это обычно принято. Дефицитность здесь понимается с точки зрения вклада ресурса в увеличение выпуска продукции при его дополнительном увеличении.

А из соотношений (2.9) следует, что если ресурс в оптимальном плане не израсходован (расход меньше запаса), то его оценка равна нулю. Такой ресурс будем называть недефицитным – его увеличение не приведёт к увеличению выпуска продукции в оптимальном плане.

Таким образом, 2-е свойство можно сформулировать так: в оптимальном плане дефицитный ресурс имеет положительную оценку, и чем больше оценка, тем ресурс дефицитней. Недефицитный ресурс имеет нулевую оценку. Подчеркнём ещё раз, что под дефицитностью здесь понимается вклад ресурса в достижение поставленной цели.

Свойство 3. Оценка как мера эффективности выпускаемой продукции.

Это свойство следует из соотношений (2.10) и (2.11). В соответствии с (2.11) в оптимальном плане выпускается та продукция (выпуск больше нуля, т.е.

), оценка суммарных затрат ресурсов на выпуск единицы которой равна цене единицы этого продукта. Такую продукцию будем называть рентабельной. А в соответствии с (2.10) продукция в оптимальном плане не выпускается

22

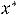
(), если оценка ресурсов на выпуск единицы такой продукции больше цены. Под рентабельностью здесь понимается равенство оценки ресурсов на выпуск единицы продукции цене единицы этой продукции.

Таким образом, это свойство можно сформулировать так: в оптимальный план включается выпуск только рентабельной продукции.

Свойство 4. Оценка как средство балансировки затрат и результатов в оптимальном плане.

Это свойство следует из теоремы 1. В соответствии с этой теоремой объём выпуска продукции в оптимальном плане (результат производства) равен оценке имеющихся ресурсов. Известно, что если план неоптимальный, то Z = W = , т.е. «затраты» превышают результат.

Проиллюстрируем эти свойства на конкретном примере.

При этом будем ориентироваться на решении задачи ЛП с помощью пакета прикладных задач QM for Windows. Как известно, задача ЛП решается симплексным методом, который представляет собой метод последовательного улучшения плана и реализуется в виде последовательных итераций. При необходимости эти итерации можно вывести на экран и распечатать.

В этом пакете программа (ЛП) позволяет решать задачи ЛП симплексным методом без каких-либо ограничений на их вид и размерностью до 90 х 90 (по числу ограничений и переменных). Если ограничения задачи заданы в виде неравенств, то кроме основных переменных для приведения задачи к основному виду программой предусмотрено введение балансовых переменных (с положительным знаком в случае неравенства вида и отрицательным – при знаке ). Обозначаются они в отчётах о решении задачи по-разному, в зависимости от того, с каким знаком вошли в ограничения. Если со знаком минус, то через “surplus” (излишек), а если со знаком плюс, то через “slack” (избыток), с соответствующими индексами. Если после введения балансовых переменных исходный базис неочевиден, то предусмотрено введение искусственных балансовых переменных. Искусственные переменные обозначаются через “artfcl”, с соответствующими индексами.

Необходимые сведения, нужные для анализа задачи, в дальнейшем будем приводить по мере необходимости.

При вводе исходной информации в диалоговом окне необходимо предварительно указать размерность задачи: число ограничений (Number of

23

Constraints) и число переменных (Number of variables), а также тип целевой функции (Objective) – на минимум или максимум.

Задания для выполнения лабораторной работы.

1.Составить модели исходной и двойственной задач.

2.Решить задачу и вывести окна об отчёте решения.

3.Проанализировать полученное решение на основе свойств двойственных оценок.

4.Проанализировать решение задачи в условиях изменения:

а) цен в границах их устойчивости; б) цен за пределами границ устойчивости;

и) запасов ресурсов а в границах устойчивости; г) запасов ресурсов за пределами границ устойчивости.

5.Проанализировать решение задачи в предположении выпуска нерентабельной продукции в объёме не менее 15 единиц.

6.Проанализировать решение задачи в условиях реализации недефицитного ресурса и приобретении наиболее дефицитного ресурса для дополнительного выпуска продукции (цена ресурса соответственно равна 5, 3, 6 и 4 у.е).

2.3. Ход выполнения работы

1. Пусть в производстве 4 видов продукции участвуют 4 вида ресурсов. Известны нормы расхода каждого вида ресурса на производство единицы каждого вида продукции, цены реализации единицы каждого вида продукции и запасы каждого вида ресурса. Требуется определить план производства продукции, максимизирующий суммарную выручку от реализации произведённой продукции.

Пусть А – матрица коэффициентов расхода ресурсов, В – запасы ресурсов и С – цены продукции.

Тогда модель сформулированной задачи примет вид: найти x1, x2, x3, x4, удовлетворяющие условиям:

24

0, (j=1,2,3,4),

и при которых функция

Z =

достигает максимума.

2. Введённая в модуль «линейное программирование» пакета QM for Windows эта задача примет вид, как на рисунке 2.1.

Рисунок 2.1 – Окно задачи с исходной информацией

Решение задачи с помощью пакета QM имеет нескольких окон. Приведём некоторые из них.

Рисунок 2.2 – Окно с исходной (Original Problem) и двойственной (Dual Problem) задачами

25

Итак, как указано в нижней части рисунка 2.2, двойственная задача заключается в нахождении двойственных оценок , (i = 1,2,3,4), удовлетворяющих условиям:

0, (i=1,2,3,4),

при которых целевая функция

W =

достигает минимума.

Окно с решением задачи имеет вид рисунка 2.3.

Рисунок 2.3 – Отчёт о решении прямой и двойственной задач

Это окно дублирует исходную задачу и приводит её решение (нижняя строка

– Solution), а также решение двойственной задачи (крайний правый столбец – Dual). Здесь же указано оптимальное значение прямой задачи (Optimal Z = 118), а, следовательно, и оптимальное значение двойственной задачи, т.к. в соответствии с торемой1 оптимальные значения прямой и двойственной задач совпадают.

Рисунок 2.4 – Подробный отчёт о решении прямой задачи

26

На рисунке 2.4 приведён подробный отчёт о решении прямой задачи. Как известно, симплексным методом можно решать канонические задачи ЛП, т.е. когда система ограничений приведена к базису, а правые части ограничений неотрицательны.

Чтобы привести нашу систему ограничений к такому виду, потребовалось в каждое неравенство ввести балансовую переменную. Обозначаются они через slack.

Таким образом, определяем, что оптимальное решение исходной (прямой) задачи равно = (0;8,3; 4; 3,7). Первая переменная в оптимальном плане равна нулю ( = 0), следовательно, не входит в базис в оптимальном решении, а остальные переменные не равны нулю, следовательно, являются базисными, что и указано в верхней части рисунка 2.4. В нижней части рисунка 2.4 указан статус балансовых переменных. Тот факт, что slack 2 = 29, означает, что в оптимальном решении левая часть второго ограничения меньше правой части на эту величину. А остальные ограничения выполняются как строгие равенства.

На рисунке 2.5 приведены границы устойчивости двойственных оценок прямой и двойственной задач. Известно, что двойственные оценки довольно устойчивы по отношению к небольшим изменениям правых частей задачи. В нашем случае для прямой задачи правые части ограничений – это запасы ресурсов, а для двойственной – цены продукции.

В силу симметричности прямой и двойственной задач переменные исходной задачи – это двойственные оценки двойственной задачи.

Итак, в верхней части таблицы 2.5 указаны границы устойчивости цен, а в нижней – запасов ресурсов.

Рисунок 2.5 – Границы устойчивости двойственных оценок

27

Структура таблицы на рисунке 2.5 следующая. Во втором столбце таблицы указаны значения переменных в оптимальном решении прямой и двойственной задач (Value/Dual Value), затем столбец значений балансовых переменных этих задач (Reduced Cost/Slack), затем столбец значений правых частей ограничений этих задач (соответственно – цены продукции и запасы ресурсов) и, наконец, нижняя и верхняя границы устойчивости этих величин. Пока цены продукции и запасы ресурсов, изменяясь, не выйдут за пределы этих границ, двойственные оценки прямой и двойственных задач меняться не будут.

3. Проанализируем решение нашей задачи, используя свойства двойственных оценок.

Всоответствии с первым свойством, если изменить объём первого ресурса на единицу, то оптимальное значение целевой функции (суммарный объём выпуска продукции) изменится на 3 единицы (на оценку единицы этого ресурса).

Изменение 2-го ресурса на единицу не приведёт к изменению выпуска продукции (его оценка равна нулю).

Соответственно, изменение 3-го и 4-го ресурсов на единицу приведёт к изменению объёма выпуска продукции на 0,4 единицы.

Всоответствии со вторым свойством дефицитными у нас являются 1-й, 3-й и 4-й ресурсы, т.к. их оценки в оптимальном плане положительны. Недефицитным является 2-й ресурс – его оценка равна нулю. Наиболее дефицитным является 1-

йресурс, т.к. его оценка наибольшая.

Проверим 2-е ограничение по недефицитному ресурсу, подставив в него значения переменных из оптимального плана:

.

Получим 7*0+5*8,333+3*4+2*3,667 = 61, что меньше 90 на 29 единиц, а это и есть значение балансовой переменной во втором ограничении в оптимальном решении (см. рисунок 2.5, 3-ю снизу строку в столбце slack). Если провести проверку других ограничений, то они выполнятся как строгие равенства.

В соответствии с 3-м свойством рентабельной является продукция 2-го, 3-го и 4-го видов (выпускается соответственно в объёмах 8,3 4 и 3,7 единиц), а продукция 1-го вида не выпускается, т.е. является нерентабельной.

Проверим это, подсчитав оценку ресурсов на выпуск единицы этой продукции. Для этого подставим в первое ограничение двойственной задачи значения оценок из оптимального плана:

.

28

Получим 1*3+7*0+3*0,4+1*0,4 = 4,6, что больше 4 на величину 0,6, а это и есть значение балансовой переменной в первом ограничении в оптимальном плане (см. рисунок 2.5 первая строка сверху). Если провести проверку других ограничений, то они выполнятся как строгие равенства.

В соответствии с 4-м свойством и теоремой 1. Zmax = Wmin. Проверим это, подставив оптимальные значения переменных прямой и двойственной задач в их целевые функции.

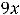
Z = Zmax = 4*0+5*8,333+9*4+11*3,666 = 118.

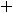
W = Wmin = 16*3+90*0+120*0,4+55*0.4 = 118.

Что и требовалось показать.

этом случае оценка ресурса не изменится и в соответствии с 1-м свойством будет показывать, насколько изменится целевая функция, если объём ресурса изменить в пределах границ устойчивости. Увеличим его запас на 3 ед., т.е. сделаем равным 16+3=19.

Решение задачи примет вид (рисунок 2.6).

Как видим, оценки ресурсов остались прежними, хотя объёмы выпуска продукции изменились. Кроме того, значение целевой функции стало равно 127, что можно было получить и не решая задачу. Изменение на единицу этого ресурса вызывает изменение Zmin на 3ед., а изменив объём ресурса на три единицы (в пределах границ устойчивости) Zmin изменится на 3*3=9 единиц, т.е. к 118 добавляется 9, чему и равна целевая функция в изменённой задаче (127).

Рисунок 2.6 – Решение задачи при изменении ресурса в границах устойчивости

29

Увеличим объём этого ресурса на 5 единиц, тем самым выйдем за пределы границ устойчивости. Получим (рисунок 2.7)

Рисунок 2.7 – Решение задачи при изменении ресурса за пределами границ устойчивости

Как и ожидалось, изменились оценки ресурсов и структура выпуска продукции (вместо первого продукта нерентабельным стал третий, а недефицитным стал первый ресурс).

Будем теперь менять цену продукции. В оптимальном плане исходной задачи нерентабельной была первая продукция. Увеличим её цену в пределах границы устойчивости, установив равной 4,5, решив задачу, получим (рисунок 2.8).

Рисунок 2.8 – Решение задачи при изменении цены в границах устойчивости

Как и ожидалось, ничего не изменилось. Первый продукт по-прежнему нерентабельный.

Изменим его цену за пределами границ устойчивости. Получим (рисунок

2.9).

30

Рисунок 2.9 – Решение задачи при изменении цены за пределами границ устойчивости

Теперь первый продукт стал рентабельным, нерентабельным – второй.

5. Предположим далее, что в условиях исходной задачи требуется выпустить нерентабельной продукции в объёме 3 единиц, не меняя её цену. Проверим, как это отразится на оптимальном плане.

У нас нерентабельная 1-я продукция, поэтому дополнительное ограничение будет иметь вид Введём дополнительную строку, в которой запишем, что х1 должен быть не менее трёх. Задача примет вид (рисунок 2.10).

Рисунок 2.10 – Условие задачи с дополнительным ограничением

Решим эту задачу (рисунок 2.11).

Как видим, первый вид продукции выпускается в объёме 3 единиц, как и было задано. Объёмы выпуска других видов продукции изменились: 2-го и 4-го видов уменьшились, а 3-го вида увеличился.

31

Рисунок 2.11 – Решение задачи с дополнительным ограничением

Оценка нового ограничения (-0,6) показывает, что выпуск единицы 1-й продукции уменьшает целевую функцию (объём выпуска продукции) на 0,6 единиц. И соответственно целевая функция уменьшилась на 3*0,6=1,8 единиц и стала равна 116,2.

6. Вернёмся к исходной задаче и зададимся целью увеличить выпуск продукции, реализовав остаток недефицитного ресурса и приобретя на полученную выручку наиболее дефицитный первый ресурс.

Пусть, например, цена первого ресурса равна 5, а второго – 3. Через x5 обозначим объём реализованного 2-го ресурса. Тогда второе ограничение примет вид

Т.е. этот ресурс расходуется на выпуск продукции плюс на продажу в объёме х5. Изменится и первое ограничение: продав второй ресурс по цене 3, выручим 3*х5. На эту сумму приобретём первый ресурс по цене 5. Объём приобретённого ресурса будет равен (3*х5)/5, т.е. 0,6х5. Таким образом, объём первого ресурса станет равным 16+0,6х5, и первое ограничение примет вид.

.

Перепишем его в виде

.

Добавим столбец для переменной х5, и задача примет вид (рисунок 2.12).

32

Рисунок 2.12 – Модель задачи с изменёнными условиями Решим её (рисунок 2.13).

этого увеличили выпуск 2-й и 4-й продукции, а выпуск 3-й продукции уменьшился, но общий объём выпуска увеличился и стал равным 1293478. Поскольку все двойственные оценки в новом плане положительны, то все ресурсы в нём израсходованы полностью (стали дефицитными).

2.4. Задания к выполнению лабораторной работы №2

Варианты заданий возьмите из этой таблицы

33

3. Лабораторная работа №3

Классическая транспортная задача и её модификации

Транспортная задача (ТЗ) является частным случаем задачи ЛП и может быть решена симплексным методом. Но, учитывая особенности модели ТЗ, разработаны специальные методы её решения. Один из таких методов, реализованный в рассматриваемой программе, называется методом потенциалов. Рассмотрим алгоритм решения ТЗ по этому методу.

Суть ТЗ состоит в нахождении плана перевозки однородного груза от поставщиков к потребителям, минимизирующего суммарные издержки по перевозке этого груза при условии вывоза его от поставщиков и удовлетворения спроса потребителей.

Математическая постановка ТЗ имеет вид:

найти совокупность переменных xij (i=1,2,...,m), (j=1,2,...n), минимизирующих целевую функцию

34

Z = i, j cij xij

при выполнении условий:

здесь xij – объёмы перевозок груза от i-го поставщика к j-му потребителю; cij – транспортные издержки по перевозке единицы груза;

задачи называется закрытой. Алгоритм решения ТЗ разработан для закрытых моделей, но при необходимости открытую модель легко привести к закрытой,

участия пользователя.

Решение ТЗ начинается с нахождения начального плана перевозок. Разработано несколько способов их нахождения. В программе QM реализовано три метода нахождения начального плана: метод северо-западного угла

(Northwest Corner Method), метод минимальной стоимости (Minimum Cost Method), приближенный метод Вогеля (Vogel`s Approximation Method), и, если при выборе метода нахождения начального решения указать процедуру “Any Starting Method”, то программой выбирается лучший из трёх перечисленных с точки зрения значения целевой функции (обычно это – метод Вогеля).

Каждый из перечисленных методов нахождения начального допустимого решения ТЗ имеет свои преимущества и недостатки, и выбор того или иного из них зависит от исходной информации. Не обсуждая подробно каждый из них, заметим, что метод северо-западного угла даёт начальное решение, расположенное в таблице транспортной задачи в направлении от левого верхнего угла к правому нижнему, и поэтому им рекомендуется пользоваться, если транспортные издержки минимальны в области этой диагонали таблицы.

35

Метод минимальной стоимости, как правило, даёт лучшее исходное решение, если клетки таблицы ТЗ, содержащие наименьшие транспортные тарифы, расположены вне пределов такой диагонали таблицы. Приближенный метод Вогеля основан на понятии вмененных издержек, и начальное решение, полученное на его основе, как правило, даёт решение, наиболее близкое к оптимальному.

Для проверки оптимальности плана в методе потенциалов используются характеристики свободных клеток таблицы ТЗ. Рассчитываются они как разность между тарифом клетки и суммой потенциалов соответствующих строк и столбцов:

Eij = cij – (ui + vj),

где Eij – характеристика свободной клетки (i,j); ui – потенциал i-й строки; vj – потенциал j-го столбца.

Потенциалы строк и столбцов находятся из системы уравнений: cij = ui + vj ,

составленной по занятым клеткам таблицы. Известно, что число занятых клеток

исоответственно уравнений равно m + n – 1, а число переменных ТЗ на единицу больше. Следовательно, данная система уравнений имеет одну степень свободы

идля нахождения её фиксированного решения одну из переменных необходимо зафиксировать на определённом уровне.

Характеристики свободных клеток не зависят от того, на каком уровне зафиксирована одна из таких переменных, поэтому в отчётах о решении задачи указываются только характеристики. Их смысл состоит в том, что они показывают, насколько изменится целевая функция, если в соответствующую свободную клетку перераспределить поставку, равную единице. Если характеристики свободных клеток неотрицательны, то соответствующий план ТЗ является оптимальным. В противном случае в клетку, имеющую наименьшую отрицательную характеристику, осуществляется перераспределение максимально возможной поставки по контуру, построенному для этой клетки.

Как уже указывалось, ТЗ имеет команду Step, позволяющую поэтапно проследить решение задачи от итерации к итерации. К тому же, если ТЗ имеет неединственное оптимальное решение, то все базисные оптимальные решения можно получить, лишь используя эту команду. Если задачу решить с помощью команды Solve, то в отчёте о решении будет указано последнее оптимальное решение, предыдущие, если они существуют, не отражаются.

36

Проиллюстрируем решение ТЗ с использованием предлагаемой программы. В диалоговом окне для создания нового файла необходимо кроме заголовка (Title) указать число источников (поставщиков) (Number of Sources) и число пунктов назначения (Number of Destinations). После ввода этой информации необходимо заполнить появившуюся таблицу исходных данных задачи. В клетки таблицы вносим тарифы, в последнюю строку (DEMAND) заносим спрос потребителей, а в последний столбец (SUPPLY) – запасы поставщиков.

3.1. Классическая транспортная задача

Пусть решается следующая задача (рисунок 3.1).

Рисунок 3.1 – Окно исходных данных ТЗ Центральная часть таблицы – это тарифы по перевозке единицы груза от

поставщика к потребителю. Последний столбец (SUPPLY) – запасы груза у поставщика, последняя строка (DEMAND) – спрос потребителя. Как видим, суммарный спрос равен 100, а суммарное предложение – 95 ед. груза. Начальный метод заполнения исходного решения – метод минимальной стоимости.

Решив задачу, можно вывести на экран и сохранить следующие окна:

Рисунок 3.2 – Оптимальный план перевозки груза

37

В этом окне (рисунок 3.2) отражены поставки груза в оптимальном решении ТЗ (от поставщиков к потребителям). В правом верхнем углу отчёта как примечание отмечено, что задача имеет несколько оптимальных решений. В заголовке таблицы указано значение целевой функции в оптимальном решении (Optimal solution value = $720) – это минимальная стоимость по перевозке . Кроме того, в верхней части отчёта указан метод нахождения начального решения.

Отметим, что, как видно из приведённого отчёта, алгоритм решения задачи ввёл в рассмотрение дополнительного поставщика (последняя строка Dummy) с предложением, равным 5, и поставка от этого поставщика 5-му потребителю означает его неудовлетворённый спрос.

Как отмечалось, алгоритм решения ТЗ предусматривает равенство суммарного предложения и суммарного спроса и в случае нарушения этого условия вводятся либо фиктивный поставщик (как в нашем случае), либо фиктивный потребитель (если суммарное предложение больше суммарного спроса) с нулевыми тарифами.

Следующее окно (рисунок 3.3) – это оценки свободных клеток таблицы ТЗ в оптимальном решении.

Рисунок 3.3 – Оценки свободных клеток

Эти оценки являются аналогом двойственных оценок задачи ЛП и показывают, насколько изменится целевая функция, если в соответствующую клетку таблицы перераспределить поставку, равную единице. Поскольку все оценки неотрицательны, то это и есть оптимальных план – любое его изменение не приведёт к уменьшению общих затрат по перевозке груза от поставщиков к потребителям. По этой же информации можно судить о числе оптимальных базисных решений – по числу нулевых оценок: в этом примере имеем три оптимальных базисных решения.

38

3.2. Транспортная задача с ограничениями

Предположим, что 3-й поставщик и 3-й потребитель не связаны между собой прямым маршрутом и поставка между ними не возможна. Для решения задачи в таком виде для запрета поставки между поставщиками и потребителями вводятся «запретительные» тарифы. По сути это «большие» тарифы и алгоритм ТЗ поставку в эту клетку не осуществит, т.к. он нацелен на минимизацию целевой функции. В нашем случае поставим равным 999. Тогда решение задачи с изменённым тарифом примет вид (рисунок 3.4).

Рисунок 3.4 – Решение ТЗ с запретом Как видим, клетка (3.3) пуста, т.е. поставка в эту клетку отсутствует, а

значение целевой функции увеличилось на 21 за счёт перераспределения поставок по менее выгодным маршрутам.

3.3. Двухэтапная транспортная задача

Предположим, что груз непосредственно между поставщиками и потребителями не может. Его сначала нужно завезти на склады, а затем со складов развезти потребителям. В этом случае имеем двухэтапную ТЗ – на первом этапе завезти груз на склады, а на втором – развезти груз со складов потребителям.

Не приводя теоретической модели такой задачи, покажем на примере метод её решения.

Пусть имеются три поставщика готовой продукции, которую нужно развезти четырём потребителям через два склада.

Затраты по перевозке продукции от поставщиков на склады и со складов

Будем считать, что запасы груза у поставщиков равны соответственно 50, 30 и 20 единиц, вместимость складов – 50 и 60 единиц, а потребности потребителей

– 20, 25, 30 и 25 единиц груза.

39

Тогда таблица двухэтапной ТЗ примет вид (рисунок 3.4)

Рисунок 3.4 – Исходная таблица двухэтапной ТЗ

Здесь структура модели следующая.

Первый блог коэффициентов (три источника и два пункта назначения – верхние левые три строки и два столбца) – это ТЗ по перевозке груза от поставщиков на склады, следующие 4 столбца (у первых трёх строк) – это как бы поставки груза со складов потребителям, клетки заполнены запретительными тарифами (эти поставки запрещены).

Следующие две строки таблицы (Source 4 и Source 5) – это связи складов самих с собой и с потребителями. Первые два столбца – это связи складов самих с собой. Между разными складами связи запрещены – стоят запретительные тарифы, связи складов самих с собой отмечены нулевыми тарифами – поставки не производятся. Это грузы, которые якобы остаются на складах, а на самом деле – мощности складов, не используемые в решении задачи. Диагональ с нулевыми тарифами называется фиктивной. Следующие 4 столбца в этих двух строках – это поставки груза со складов потребителям.

Решение данной задачи следующее (рисунок 3.5).

Рисунок 3.5 – Решение двухэтапной ТЗ Получили, что от поставщиков на склады груз развезли так: 50 ед. груза от

первого поставщика перевезли на первый склад, от 2-го и 3-го поставщиков грузы завезли на второй склад – это 50 ед. груза (30 – от 2-го поставщика и 20 – от 3-го)

40

Второй склад загружен не полностью, что отражено в фиктивной диагонали – 10 ед. груза на пересечении Source 5 и Destination 2 (это связь второго склада самого с собой).

В последних двух строках (начиная со столбца Destination 3) отражены перевозки груза со складов потребителям.

Суммарная оптимальная стоимость этих перевозок показана в заголовке таблицы – 1050.

3.4. Задания к выполнению лабораторной работы №3

41