502_KHramova_T._V._Diskretnaja_matematika_proektirovanie_konechnykh_avtomatov_v_primerakh_i_zadachakh_
.pdfФедеральное агентство связи Федеральное государственное образовательное бюджетное учреждение высшего профессионального образования «Сибирский государственный университет телекоммуникаций и информатики» (ФГОБУ ВПО «СибГУТИ»)
Т.В. Храмова
Дискретная математика: проектирование
конечных автоматов в примерах и задачах
Учебное пособие
Новосибирск
2014
УДК 519.1 ББК 22.1 Б516
Храмова Т. В. Дискретная математика: проектирование конечных автоматов в примерах и задачах: Учебное пособие. – Новосибирск: Изд-во СибГУТИ, 2014.
– 48с.
Учебное пособие сдержит краткие теоретические сведения, примеры и задания по теории конечных автоматов. Пособие предназначено для проведения практических занятий по дискретной математике при подготовке инженеров, а так же бакалавров и магистров (направление «Телекоммуникации»)
Кафедра высшей математики СибГУТИ
Рецензенты: д. ф.-м. н. Мальцев И.А.
к. ф.-м. н. Сибиряков Е.Б.
Для подготовки студентов по направлению 210700 «Инфокоммуникационные технологии и системы связи», квалификация (степень) бакалавра.
Утверждено редакционно-издательским советом СибГУТИ в качестве учебного пособия.
© Храмова Т.В. © Сибирский государственный университет телекоммуникаций информатики, 2014
|
|
|
Оглавление |
|
|
|
|
|
|||
Определение конечного детерминированного автомата Мили.............. |
4 |
||||||||||
Примеры построения к.д.а. Мили. |
.............................................................. |
|
|
|
|
|
5 |
||||
Пример 1. |
y(t) x(t)& x(1).......................................................................... |
|
|
|
|
|
|
|
|
5 |
|
Пример 2. |
y(t) x(t) x(2), |
y(1) . |
0 ....................................................... |
|
|
|
|
|
8 |
||
Пример 3. |
y(t) x(t) x(1) x(2), ............................................. |
y (1) 1 |
|
|
|
10 |
|||||
Пример 4. |
y(t) x(t) ~ x(t 1), |
y(1) . ...................................................1 |
|
|
|
|
|
14 |
|||
Пример 5. |
y(t) x(t) x(t 1) x . .....................................(1), |
y(1) 0 |
|
|
|
16 |
|||||
Пример 6. |
y(t) x(t) x(t 1) ~ x . ...............(t 2), |
y(1) 0, |
y(2) 0 |
20 |
|||||||
Пример 7. |
y(t) x(t) x(t 2), |
y . ...............................(1) 1, |
y(2) |
1 |
|
23 |
|||||
Пример 8. |
y(t) x(t) x(t 1) x(t ... . ...........................................2) |
x(1) |
|
|
|
25 |
|||||
|
x(1) x(3) x(5) ... |
x(t), |
t нечетный, |
|
|||||||
Пример 9. |
y(t) |
|
|
.............. |
|
|
|
|
|
|
26 |
|
x(1) x(3) x(5) ... |
x(t 1), |
t четный. |
|
|||||||
|
x(t) 1, |
t нечетный, |
|
|
|
|
|
||||
Пример 10. |
y(t) |
|
|
........................................ |
|
|
|
|
|
|
29 |
|
x(t) x(t 1), |
t четный . |
|
|
|
|
|||||
Пример 11. y(t) x1(t) x2(1) |
.................................................................... |
|
|
|
|
|
|
|
31 |
||
Пример 12. y(t) x1(t) x2(t 1), . .............................................. |
y (1) |
1 |
|
|
|
|
33 |
||||
Пример 13. y(t) x1(t) x2(1) x1(t . ......................................1), |
y(1) 0 |
|
|
|
35 |
||||||
Пример 14. |
y(t) x2(t) x1(t 2), |
y (1) x 2 (1), y (2) |
x2(2)...................37 |
||||||||
Примеры построения к.д.а. Мура.............................................................. |
|
|
|
|
|
|
40 |
||||
Пример 15. y(t) 1010101010.................................................................... |
|
|
|
|
|
|
|
40 |
|||
Пример 16. y(t) 1010001010001010001.................................................. |
|
|
|
|
40 |
||||||
Построение автоматов-распознавателей . .....................................языка |
|
|
|
42 |
|||||||
Пример 17. LV {ab,abab,...,ab... |
ab ....................................,...},V {a,b} |
|
|
42 |
|||||||
Пример 18. LV {ab,cca},V {a,b, ........................................................c} |
|
|
|
|
|
43 |
|||||
Пример 19. LV { | содержит подслова . ......ab или cca},V {a,b,c} |
43 |
||||||||||
Пример 20. LV { | содержит подслово ......................aba},V {a,b} |
45 |
||||||||||
Пример 21. LV { | |
четное число .........................},V {0,1,2,...,9} |
46 |
|||||||||
Пример 22. LV { | |
число, кратное ...................3},V {0,1,2,...,9} |
46 |
|||||||||
Пример 23. LV { | |
число, кратное ...................4},V {0,1,2,...,9} |
46 |
|||||||||
Задачи для самостоятельного решения. ................................................... |
|
|
|
|
|
47 |
|||||
СПИСОК ЛИТЕРАТУРЫ .......................................................................... |
|
|
|
|
|
|
|
|
47 |
||
3
Определение конечного детерминированного автомата Мили
Конечный детерминированный автомат Мили 
X,Y,S, ,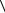 
(к.д.а.)
определяется входным алфавитом X {x1,x2,...xn}, выходным алфавитом
Y {y1,y2,...ym}, алфавитом |
состояний |
|
S {s0,s1,s2,...sk}, |
функцией |
переходов : X S S из |
состояния в состояние и функцией выхода |
|||
: X S Y . К.д.а. можно |
представить |
в |
виде диаграммы |
Мура (1), |
таблицы переходов-выходов (2), канонической таблицы (3) и канонических уравнений (4):
(1)
|
|
|
|
|
|
|
|
|
|
(2) |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
s1(t) |
… |
sm(t) |
x1(t) |
… |
xk (t) |
y1(t) |
… |
yl(t) |
s1(t 1) |
|
… |
sm(t 1) |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t ,x t ; |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||||
|
|
y t s |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
t 1,2,3.... |
(4) |
|
||||||
|
|
s t 1 s t ,x t . |
|
||||||||||||
Структуры (1) — (4) удобно задавать последовательно, друг за другом. Если функция выхода зависит только от состояния и не зависит от
входного символа, то к.д.а. называют автомат Мура.
Автомат-распознаватель языка — это автомат Мили без выходного алфавита и, следовательно, без функции выхода. В автомате распознавателе языка выделены несколько «заключительных» состояний, в которые он переходит, получив на входе «допустимое» слово.
4
Примерыпостроенияк.д.а.Мили.
Во всех задачах построить к.д.а., реализующий функцию: определить множества S,X,Y , построить таблицу и диаграмму Мура, построить каноническую таблицу, канонические уравнения.
Пример 1. y(t) x(t)& x(1).
Решение. Входной и выходной алфавиты автомата {0;1}. Кроме начального состояния S0 требуется еще два состояния S1 и S2, в которые автомат переходит в зависимости от символа, введенного на первом такте. Построим диаграмму Мура (рисунок 1).
Рисунок 1.
Следуя диаграмме Мура, составим таблицу переходов-выходов:
|
x(t) |
0 |
1 |
S |
|
||
|
S0 |
S1 |
S2 |
|
0 |
1 |
|
|
|
||
|
S1 |
S1 |
S1 |
|
0 |
0 |
|
|
|
||
|
S2 |
S2 |
S2 |
|
0 |
1 |
|
|
|
||
|
|
5 |
|
В соответствие состояниям поставим последовательности из «0» и «1. Поскольку состояний три, последовательности будут иметь длину 2:
S |
0 |
S1S2 |
00, |
S |
S1S2 |
01, |
S |
2 |
S1S2 |
10. |
|||
|
0 |
0 |
|
1 |
1 |
1 |
|
|
2 |
2 |
|
||
Последовательность «11» остается неиспользованной. Составим каноническую таблицу:
Si1(t) |
Si2(t) |
x(t) |
y(t) |
Si1(t 1) |
Si2(t 1) |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
— |
— |
— |
1 |
1 |
1 |
— |
— |
— |
Определение недостающих элементов в канонической таблице тесно связано с составлением канонических уравнений. Рассмотрим несколько вариантов.
Вариант 1. Запишем СДНФ для y(t), Si1(t 1) |
и Si2(t 1): |
|
|
|||||||||||||||||||||||||||||||||
y(t) |
|
|
|
|
|
|
|
|
|
x(t) S1(t) |
|
|
|
x(t), |
|
|
|
|
|
|
|
|
|
|||||||||||||
S1(t) |
S2(t) |
S2(t) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
i |
i |
|
|
|
i |
i |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Si1(t 1) Si1(t) Si2(t) x(t) Si1(t) Si2(t) x(t) Si1(t) Si2(t) x(t), (5) |
||||||||||||||||||||||||||||||||||||
S |
2 |
|
|
|
|
|
|
|
|
|
S2(t) |
|
|
|
|
S2 |
|
|||||||||||||||||||
(t 1) |
S1 |
(t) |
|
S2 |
(t) |
|
|
|
S1 |
(t) |
|
|
S1 |
(t) |
(t) x(t). |
|||||||||||||||||||||
x(t) |
x(t) |
|||||||||||||||||||||||||||||||||||
|
i |
|
|
|
|
i |
|
|
|
|
|
i |
|
|
|
|
|
i |
|
|
|
i |
|
|
|
i |
|
|
i |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По каноническим уравнениям (5) можно доопределить «недостающие» элементы канонической таблицы:
Si1(t) |
Si2(t) |
x(t) |
y(t) |
Si1(t 1) |
Si2(t 1) |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
Вариант 2. Запишем СДНФ для y(t), Si1(t 1), упростим их выше приведенным способом. Для составления уравнения Si2(t 1) используем тот факт, что значения в столбце, соответствующем Si2(t 1)
противоположны значениям в столбце, соответствующем Si1(t 1):
6
y(t)
1
Si (t
Si2(t
Si2(t) x(t), |
|
1) Si1(t) x(t) Si1(t) Si2(t), |
(6) |
1) Si1(t) x(t) Si1(t) Si2(t).
Тогда «недостающие» элементы доопределим в соответствии с (6):
|
Si1(t) |
Si2(t) |
x(t) |
y(t) |
Si1(t 1) |
Si2(t 1) |
|
|
|
0 |
0 |
0 |
0 |
0 |
1 |
|
|
|
0 |
0 |
1 |
1 |
1 |
0 |
|
|
|
0 |
1 |
0 |
0 |
0 |
1 |
|
|
|
0 |
1 |
1 |
0 |
0 |
1 |
|
|
|
1 |
0 |
0 |
0 |
1 |
0 |
|
|
|
1 |
0 |
1 |
1 |
1 |
0 |
|
|
|
1 |
1 |
0 |
0 |
0 |
1 |
|
|
|
1 |
1 |
1 |
0 |
0 |
1 |
|
|
Вариант 3. |
Запишем |
СДНФ |
для y(t |
) и СКНФ для Si1(t 1) |
и Si2(t 1): |
|||
y(t)
Si1(t
Si2(t
Si1(t) Si2(t) x(t) Si1(t) Si2(t) x(t),
1) Si1(t) Si2(t) x(t) Si1(t) Si2(t)
1) Si1(t) Si2(t) x(t) Si1(t) Si2(t)
x(t) Si1(t) Si2(t) x(t) , (7)
x(t) Si1(t) Si2(t) x(t) .
Тогда каноническая таблица, согласно (7) будет доопределена следующим образом:
Si1(t) |
Si2(t) |
x(t) |
y(t) |
Si1(t 1) |
Si2(t 1) |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
|
1 |
1 |
0 |
0 |
0 |
1 |
|||
0 |
1 |
0 |
0 |
0 |
1 |
|
|
|
0 |
0 |
1 |
0 |
1 |
1 |
|||
|
|
|
0 |
1 |
0 |
1 |
0 |
0 |
|||
|
|
|
1 |
1 |
0 |
1 |
0 |
1 |
|||
|
|
|
0 |
1 |
1 |
1 |
1 |
0 |
|||
|
|
|
0 |
1 |
1 |
1 |
1 |
1 |
Можно продолжить перечисление вариантов, комбинируя предложенные выше способы. Также можно сначала доопределить элементы таблицы, а затем составлять уравнения.
7
Пример 2. y(t) x(t) x(2), |
y(1) 0. |
Решение. Входной и выходной алфавиты автомата {0;1}. Выходное значение зависит от символа, введенного на втором такте и от символа, вводимого на текущем такте. Следовательно, кроме начального состояния S0 требуется состояние «ожидания» второго такта S1, определяющего последующую деятельность и еще два состояния S2 и S3, в которые автомат переходит в зависимости от символа, введенного на втором такте: S1 — «устройство ожидает второго такта»,
S2— «устройство зафиксировало, что x(2) 0 и далее вычисляет выходные значения по формуле y(t) x(t) 0 x(t) 0 x(t)»,
S3 — «устройство зафиксировало, что x(2) 1 и далее вычисляет выходные значения по формуле y(t) x(t) 1 1».
Построим диаграмму Мура (рисунок 2).
Рисунок 2.
Следуя диаграмме Мура, составим таблицу переходов-выходов:
8
|
x(t) |
|
|
S |
|
0 |
1 |
|
S0 |
S1 |
S1 |
|
0 |
0 |
|
|
|
||
|
S1 |
S2 |
S3 |
|
1 |
0 |
|
|
|
||
|
S2 |
S2 |
S2 |
|
1 |
0 |
|
|
|
||
|
S3 |
S3 |
S3 |
|
1 |
1 |
|
|
|
Закодируем состояния и составим каноническую таблицу:
S0 S01S02 00, S1 S11S12 01, S2 S21S22 10, S3 S31S32 11.
Si1(t) |
Si2(t) |
x(t) |
y(t) |
Si1(t 1) |
Si2(t 1) |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
|
0 |
0 |
1 |
0 |
0 |
1 |
|||
|
|
|
1 |
1 |
0 |
0 |
1 |
0 |
|||
|
|
|
0 |
1 |
1 |
0 |
1 |
1 |
|||
|
|
|
1 |
1 |
0 |
1 |
0 |
0 |
|||
|
|
|
0 |
1 |
0 |
1 |
0 |
1 |
|||
|
|
|
1 |
1 |
1 |
1 |
1 |
0 |
|||
|
|
|
1 |
1 |
1 |
1 |
1 |
1 |
Составим канонические уравнения. Для y(t) |
удобно использовать СДНФ: |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2(t) |
|
|
|
|
S1(t) |
|
|
|
|
|
|
|
|
S1(t) S2 |
|
|
|
S1(t) S |
2(t) x(t) |
|||||||||||||||||||
y(t) |
S1(t) S |
|
|
|
|
S2 |
(t) |
|
|
|
|
(t) |
|
|
||||||||||||||||||||||||||||||
x(t) |
x(t) |
x(t) |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
i |
i |
|
|
i |
|
|
|
i |
|
|
|
|
|
|
|
i |
|
|
i |
|
|
|
|
i |
i |
||||||||||||||||
|
|
Si2(t) Si1(t) |
|
|
|
|
|
|
|
Si1(t) Si2(t). |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Si1(t) |
Si2(t) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
x(t) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Для Si1(t 1) |
и Si2(t 1) удобно использовать СКНФ: |
|
||||||||||||||||||||||||||||||||||||||||||
Si1(t 1) Si1(t) Si2(t) x(t) Si1(t) Si2(t) |
|
|
Si1(t) Si2(t), |
|
||||||||||||||||||||||||||||||||||||||||
x(t) |
|
|||||||||||||||||||||||||||||||||||||||||||
Si2(t 1) Si1(t) |
|
|
x(t) |
|
Si2(t) x(t) |
|
Si2(t) |
|
) |
|||||||||||||||||||||||||||||||||||
Si2(t) |
Si1(t) |
Si1(t) |
||||||||||||||||||||||||||||||||||||||||||
x(t |
||||||||||||||||||||||||||||||||||||||||||||
Si1(t) |
|
x(t) |
|
|
Si2(t) . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Si2(t) |
Si1(t) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
Составим систему канонических уравнений: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
1 |
|
2 |
(t) |
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
y(t) Si |
(t) Si |
Si |
(t) Si (t) x(t) |
Si |
(t) Si (t), |
|
|||||||||||||||||||||||||||||||||
1 1 2
Si (t 1) Si (t) Si (t),
Si2(t 1) Si1(t) Si2(t) x(t) Si1(t) Si2(t) .
9
Пример 3. y(t) x(t) x(1) x(2), |
y(1) 1. |
Решение. Входной и выходной алфавиты автомата {0;1}. Выходное значение определяется символами, введенными на первом и втором такте и символом, вводимом на текущем такте. Кроме начального состояния S0 требуются состояния S1 (если x(1) 0) и S2 (если x(1) 1), определяющие действия устройства после первого такта и еще четыре состояния S3 (если x(1) 0,x(2) 0), S4 (x(1) 0,x(2) 1) и S5 (x(1) 1,x(2) 0), S6 (x(1) 1,x(2) 1): S1 : y(2) x(2) x(1) x(2) 0 0 0 0,
S2 : y(2) 1 0 1 1, S3 : y(t) x(t) 0 0 0,
S4 : y(t) x(t) 0 1 x(t), S5 : y(t) x(t) 1 0 0,
S6 : y(t) x(t) 1 1 x(t).
Построим диаграмму Мура (рисунок 3).
Рисунок 3.
Составим таблицу переходов-выходов:
10