
Дискретка / diskretochka (1)
.pdf
|
0 = , 1 |
= |
|
|
+ = , = − 2 , = 3 − , = + + 2 |
||
2 + 3 = |
1 |
2 |
|
|
|
||
Решение линейного рекуррентного соотношение второго порядка в случае равных
корней: |
= – |
два |
корня |
характеристического уравнения. |
Тогда + = |
|||||||
|
1 |
|
|
|
2 |
|
|
|
|
|
1 |
2 |
+ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
Покажем, что |
= – решение рекуррентного соотношения. |
|
||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
+ 2 = + 2 +2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
= −2, |
|
= 2 – корни по теореме Виетта. |
|
|
|
|
||||||
2 |
1 |
1 |
|
1 |
|
|
|
|
|
|
|
|
+ 2 = 2 + 1 − 2 ( ) |
|
|
|
|
||||||||
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
2 + 1 |
+1 |
− 2 |
= 2 +2 + 1 |
− 2+ |
= +2 |
2 + 2 − |
|
|||||
1 |
|
|
|
|
1 |
1 |
1 |
1 |
1 |
1 |
|
|
|
|
|
= +2( + 2) |
|
|
|
|
|
||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
= |
, |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
= |
+ – тоже решение |
|
|
|
|
||||||
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
0 |
= , |
|
1 |
= . |
|
|
|
|
|
|
|
|
Если у нас есть линейное рекуррентное соотношение второго порядка, то его решением является:
1. |
Выписывается характеристическое уравнение и находятся его корни. |
|||
|
≠ , то = + (а) |
|||
2. |
1 |
2 |
1 |
2 |
= , то = + (б) |
||||
|
1 |
2 |
1 |
1 |
17. Теорема об общем решении линейных рекуррентных соотношений с постоянными коэффициентами k- го порядка. Решение
рекуррентных соотношений с постоянными коэффициентами k- го порядка с помощью характеристического уравнения.
Теорема (об общем решении линейного рекуррентного соотношения k-ого
порядка) |
Пусть |
, |
, … , – |
действительные |
корни линейного |
рекуррентного |
|||||
|
|
|
|
1 |
2 |
|
|
|
|
|
|
соотношения |
k-ого |
|
порядка |
+ |
= 1 + − 1 + 2 + − 2 + + |
||||||
|
( ) и других корней нет. Тогда общее решение имеет вид = |
+ + |
|||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
= |
+ |
+ |
2 + + |
−1 |
−1 |
, где – корень кратности m. |
||||
|
0 |
1 |
|
2 |
|
|
|
|
|
|
|
= + |
|
|
|
|
|
|
|
|
|||
|
|
1 |
2 |
|
|
|
|
|
|
|
|
= + |
= ( + ) |
|
|
|
|
||||||
|
|
1 |
1 |
|
|
1 |
|
|
|
|
|
Метод решения Л.Р.С. k-го порядка с пост. коэф.
Записать и решить характеристическое уравнение для Л.Р.С. k-го порядка.
На основании т. об общем решении записать общее решение данного Р.С. (теорема выше)

Если заданы нач. условия, то найти значения констант, которые удовлетворяют нач. задан. условиям.
18.Производящая функция. Сумма производящих функций, операция подстановки.

19.Произведение и деление производящих функций.

20. Теорема о разложении функции.

21.Теорема о производящей функции для последовательности, задаваемой линейным рекуррентным соотношением. Теорема о
рациональной производящей функции.

22.Решение рекуррентных соотношений с помощью производящих функций.
23.Ориентированные и неориентированные графы.
Ориентированным графом называется пара  , где
, где  - конечное множество вершин, а
- конечное множество вершин, а  – отношение смежности, а матрица
– отношение смежности, а матрица  называется матрицей смежности. Пара (u,v) называется дугой орграфа, с началом u и концом v.
называется матрицей смежности. Пара (u,v) называется дугой орграфа, с началом u и концом v.
Неориентированным графом называется пара 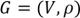 , где
, где  симметричное и антирефлексивное отношение.
симметричное и антирефлексивное отношение. 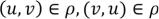 - симметричность.
- симметричность.  – антирефлексивность.
– антирефлексивность.
Симметризация орграфа (превращение в граф) – неориентированный граф (без дуг и петель)  , где
, где  тождественное отношение (исключение петли).
тождественное отношение (исключение петли).
Ворграфе степенью исхода вершины v называется число  - равное количеству дуг, исходных из v.
- равное количеству дуг, исходных из v.  .
.
Ворграфе степенью захода вершины v называется число 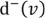 - равное количеству
- равное количеству
дуг, входящих в v. |
. |
Спецификацией |
орграфа называется последовательность такого вида: если |
 , то спецификация:
, то спецификация:  , где
, где  и
и  . Если неориентированный граф, то
. Если неориентированный граф, то 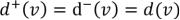 .
.
Если вершина не имеет ребер (в графе), или дуг (в орграфе), то она называется
изолированной. 
Для неориентированного графа:
1)Степенное множество графа – набор степеней его вершин. {1,2,…,n}

2)Вектор степеней графа – вектор, компонентами которого являются степени всех вершин графа, записанных по убыванию. (3,3,2,1)
24.Полный граф, дополнение, объединение, соединение графов.
Полный граф – граф, в котором любые две вершины соединены ребром  .
.
Дополнение графа -  . Объединение графов -
. Объединение графов - 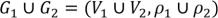 Соединение графов -
Соединение графов - 
25.Теорема о степенном множестве.
Теорема о степенном множестве. Для любого множества натуральных чисел
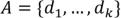 , где
, где  , найдется граф, число вершин которого равно
, найдется граф, число вершин которого равно  и для которого множество
и для которого множество 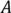 является степенным множеством.
является степенным множеством.
Доказательство.
По индукции.
Рассмотрим в качестве искомого графа – верно. |
|
||
Рассмотрим в качестве искомого графа |
(то есть |
) |
|
|
. Где – число вершин 1-ого графа, |
– число |
|
вершин 2-го графа, соответственно |
максимальная степень |
вершины 1-ого |
|
графа, |
– максимальная степень вершины 2-го графа. |
|
|
Для и теорема справедлива. |
|
|
|
Предположим, что она справедлива для чисел  . Докажем, что теорема справедлива для чисел
. Докажем, что теорема справедлива для чисел 
.
Найдется граф, у которого число вершин будет  , и у которого это множество будет степенным множеством.
, и у которого это множество будет степенным множеством.
Рассмотрим множество натуральных чисел:
, где 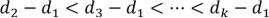 . Число чисел <k , то есть найдется граф, у которого число вершин равно
. Число чисел <k , то есть найдется граф, у которого число вершин равно  и оно является степенным множеством.
и оно является степенным множеством.  число вершин равно
число вершин равно 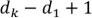 .
.
Рассмотрим граф, построенный следующим образом: . Посчитаем число вершин
. Посчитаем число вершин  . Покажем, что это действительно степенное множество этого графа
. Покажем, что это действительно степенное множество этого графа
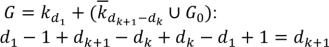 . Такое число есть в множестве.
. Такое число есть в множестве.

 – это степень вершины из
– это степень вершины из  . Граф
. Граф  может иметь любое число вершин из
может иметь любое число вершин из 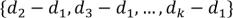 .
.
Предположим, оно равно  , тогда
, тогда  , такое число есть.
, такое число есть.
=>Для любого натурального множества  найдется граф, у которого это множество будет степенным, и т.д.
найдется граф, у которого это множество будет степенным, и т.д.
26.Теорема о соотношении суммы степеней вершин и числа ребер
(лемма о рукопожатии.)
Теорема. Лемма о рукопожатии.
В графе справедливы утверждения:
1)сумма степеней всех вершин равна удвоенному числу ребер (число ребер-m).
2)количество нечетных вершин четно.
3)если в графе  вершин
вершин  , то мощность степенного множества не превышает
, то мощность степенного множества не превышает  , (то есть, по крайней мере, 2 вершины имеют одинаковую степень)
, (то есть, по крайней мере, 2 вершины имеют одинаковую степень)
Четная вершина графа – вершина с четной степенью.
Нечетная вершина графа – вершина с нечетной степенью.
Доказательство.
1)Очевидно.
2)
3)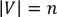
Возможные степени вершин:  у графа всего
у графа всего  чисел, числа 0 и
чисел, числа 0 и 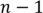 встретиться одновременно не могут => есть изолированная вершина => степень не может быть
встретиться одновременно не могут => есть изолированная вершина => степень не может быть  .
.
27.Алгоритм построения графа, по вектору степеней.
Пусть  – вектор степеней какого-то графа. Алгоритм построения:
– вектор степеней какого-то графа. Алгоритм построения:
1)Изображается n точек, и им присваиваются метки:  . В качестве начальной точки, выбирается 1-вая и ей присваивается значение
. В качестве начальной точки, выбирается 1-вая и ей присваивается значение  2)Начальная точка соединяется линиями с другими точками, в порядке убывания их меток.
2)Начальная точка соединяется линиями с другими точками, в порядке убывания их меток.
3)Метка начальной точки кладется равной 0, метки всех точек, соединенных с начальной уменьшаются на 1.

4)Если метки всех точек равны 0, то конец алгоритма. Иначе, в качестве начальной точки, выбрать точку с максимальной меткой (одну из них),  положить равной метке точки, выбранной в качестве начальной.
положить равной метке точки, выбранной в качестве начальной.
28.Изоморфизм графов. Теорема об изоморфизме графов.
Пусть даны графы:  .
.
Взаимно-однозначное соответствие  называется изоморфизмом, если оно сохраняет отношение смежности:
называется изоморфизмом, если оно сохраняет отношение смежности:
Доказательство.
Надо доказать:  - это означает, что:
- это означает, что:

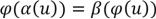 (*)
(*)
Необходимость.
29.Проверка на изоморфизм 2-х графов по их матрицам смежности.
1)Выписывается матрица  предполагаемого изоморфизма
предполагаемого изоморфизма  , как матрица с неопределенными коэффициентами.
, как матрица с неопределенными коэффициентами. 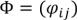 .
.
2)Составляем матричное уравнение . Решаем систему, находим
. Решаем систему, находим  . 3)Если в каждом столбце и строке ровно одна 1, то изоморфизм есть, иначе – нет.
. 3)Если в каждом столбце и строке ровно одна 1, то изоморфизм есть, иначе – нет.

4)Если вершина 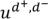 может перейти в вершину
может перейти в вершину 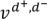 (равные степени исхода и захода) то в матрице пишем 1(если из вершины 1-ого орграфа можно лишь единожды попасть в вершину 2-го орграфа, а если не единожды – пишем:
(равные степени исхода и захода) то в матрице пишем 1(если из вершины 1-ого орграфа можно лишь единожды попасть в вершину 2-го орграфа, а если не единожды – пишем: , где
, где  – номер столбца,
– номер столбца,  – номер строки), иначе – 0.
– номер строки), иначе – 0.
30.Часть графа, подграфы. Путь, цикл, цепь, длина пути и расстояние между вершинами. Достаточное условие связности нечетных
вершин.
Подграф – часть орграфа.
Максимальный подграф орграфа – подграф, полученный удалением одной вершины из орграфа.
Путь – последовательность ребер, в которой 2 соседних ребра имеют общую вершину и ни одно ребро не встречается более 1 раза.
Простой путь – путь, котором каждая вершина принадлежит не более, чем 2 ребрам. Циклический путь – путь, в котором начальная вершина совпадает с конечной. Цикл – циклический простой путь.
Цепь - нециклический простой путь.
Длина пути – кол-во ребер, входящих в путь.
Вершины связаны, если существует путь, проходящий через них. Если вершины связаны, то найдется цепь.
По определению считают, что каждая вершина связана сама с собой, тогда отношение связности – это отношение эквивалентности. Классы отношения связности называются компонентами связности (компонентами).
Теорема. Достаточное условие связности 2 нечетных вершин.
Если 2 нечетные вершины  и
и  в графе – единственные нечетные вершины, то они связаны в графе.
в графе – единственные нечетные вершины, то они связаны в графе.
Доказательство.
От противного: пусть они лежат в разных компонентах связности, тогда в каждом подграфе (компоненте связности) есть лишь одна единственная нечетная вершина – противоречие, так как по лемме о рукопожатии: число нечетных вершин четно.
31.Достаточное условие связности графа.
Граф с универсальным отношением связности называется связным. Любые 2 вершины соединены ребром. Каждый граф является объединением своих компонентов связности.
Связный граф – граф, в котором любые 2 вершины соединены цепью.
Теорема. Достаточное условие связности.
Если в n–вершинном графе число ребер  , то граф связный.
, то граф связный.
Доказательство.
