АИГ / ALGEM_EKZ
.docx1. Алгебраические структуры
1. Бинарные отношения.
Свойство однородных бинарных отношений.
Отношение эквивалентности.
Свойство классов эквивалентности.
Пусть А и В - непустые множества.
Декартовым
произведением множества А на
множество В называется
множество
,
элементами которого являются всевозможные
пары (a, b),
где первый элемент берется из множества
А, а второй - из множества B:
.
Бинарным
отношением между
множествами А и В называется
всякое подмножество ρ декартова
произведения
:
Для
упорядоченной пары
используют
обозначение
и
говорят, что элемент a находится
с элементом b в
отношении ρ.
Если A=B, то бинарное отношение называется однородным.
Две такие пары считаются равными, если у них совпадают и первые, и вторые элементы:
Однородное бинарное отношение R на множестве А называется отношением эквивалентности, оно рефлексивно, симметрично и транзитивно.
Отношение
эквивалентности записывается как
или
.
Классом
эквивалентности соответствующим
отношению эквивалентности R на
множестве А называется
подмножество
Отношение
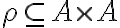называется рефлексивным,
если каждый элемент
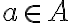находится
в этом
отношении сам с собой, т.е.
ρ
рефлексивно
Отношение называется симметричным, если пары (a, b) и (b, a) при
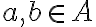одновременно
принадлежат или не принадлежат
отношению ρ:
ρ
симметрично
Отношение называется транзитивным, если ρ транзитивно
.
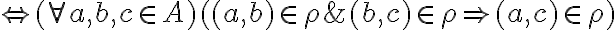Свойство классов эквивалентности
1. Каждый класс эквивалентности содержит хотя бы один элемент.
2.
Если
, то
R(b) = R(a).
3. Различные классы эквивалентности не пересекаются.
4. Объединение всех классов эквивалентности есть множество А.
2. ТЕОРЕМА О РАЗБИЕНИИ МНОЖЕСТВА С ЗАДАННЫМ ОТНОШЕНИЕМ ЭКВИВАЛЕНТНОСТИ.
Разбиением множества А на классы эквивалентности называется такое множество подмножеств данного множества, которое обладает следующими свойствами:
1. классы не пустые;
2. различные подмножества или классы не пересекаются;
3. объединение всех подмножеств дает множество А.
Теорема. Любое отношение эквивалентности порождает на множестве разбиение на классы эквивалентности.
(док-во из свойств)
ОСНОВНЫЕ ПРИМЕРЫ ОТНОШЕНИЙ ЭКВИВАЛЕНТНОСТИ (СВОБОДНЫЙ ВЕКТОР КАК КЛАСС ЭКВИВАЛЕНТНОСТИ, ОТНОШЕНИЯ КОНГРУЭНТНОСТИ НА МНОЖЕСТВЕ СВЯЗАННЫХ ВЕКТОРОВ ЕВКЛИДОВА ПРОСТРАНСТВА; ВЫЧЕТ КАК КЛАСС ЭКВИВАЛЕНТНОСТИ, ОТНОШЕНИЯ СРАВНИМОСТИ ПО MOD N НА МНОЖЕСТВЕ ЦЕЛЫХ ЧИСЕЛ).
Свободный вектор – это мн-во связанных векторов одинаковой длины и одинак. направления.
Связанные векторы AB и CD (ненулевые) называются конгруентными, если их длины и направления совпадают (когерентные)
ПОНЯТИЕ СОГЛАСОВАННОСТИ АЛГЕБРАИЧЕСКОЙ ОПЕРАЦИИ С ОТНОШЕНИЕМ ЭКВИВАЛЕНТНОСТИ.
ОСНОВНЫЕ ПРИМЕРЫ: СОГЛАСОВАННОСТЬ ОПЕРАЦИЙ СЛОЖЕНИЯ И УМНОЖЕНИЯ С ОТНОШЕНИЕМ КОНГРУЭНТНОСТИ НА МНОЖЕСТВЕ СВЯЗАННЫХ ВЕКТОРОВ.
В КУРСЕ ГЕОМЕТРИИ СВОБОДНЫЙ ВЕКТОР ОПРЕДЕЛЯЕТСЯ КАК ЭЛЕМЕНТ ФАКТОР-МНОЖЕСТВА ПО ОТНОШЕНИЮ ЭКВИВАЛЕНТНОСТИ НАПРАВЛЕНИЙ
Свободным вектором называется элемент фактор-множества V=W, т.е. элемент фактор-множества множества направленных отрезков по отношению к отношению эквивалентности .
3. ОПРЕДЕЛЕНИЕ ГРУППЫ.
Простейшие следствия из аксиом групп.
Абелевы группы.
Основные примеры: числовые множества относительно операций умножения и сложения, группа свободных векторов по сложению, матричные группы (полная линейная группа, специальная линейная группа), симметрическая группа (группа подстановок).
Определение. Группой называется множество G с операцией умножения, обладающей следующими свойствами:
1) (ab)c = a(bc), ∀a, b, c ∈ G (ассоциативность);
2) существует такой элемент e ∈ G (единица), что ae = ea = a для любого a ∈ G;
3) для всякого элемента a ∈ G существует такой элемент a^ −1 ∈ G (обрат- ный элемент), a*a^−1 = a^ −1*a = e.
Группа называется абелевой или коммутативной, если ab = ba, ∀a, b ∈ G.
Доказать, что пары (a, b) вещественных чисел, a <> 0, составляют груп- пу относительно операции (a, b)(c, d) = (ac, ad + b).
Доказательство.
1. Замкнутость операции выполняется, т.к. (a, b)(c, d) = (ac, ad+b) - пара вещественных чисел.
2. Ассоциативность: [(a, b)(c, d)](g, f) = (a, b)[(c, d)(g, f)]. Упростим левую и правую части последнего равенства: [(a, b)(c, d)](g, f) = (ac, ad + b)(g, f) = (acg, acf + ad + b) (a, b)[(c, d)(g, f)] = (a, b)(cg, cf +d) = (acg, a(cf +d)+b) = (acg, acf +ad+b). Ассоциативность операции выполняется.
3. Единичный (нейтральный) элемент данного множества - это такая пара действительных чисел (c, d), что (a, b)(c, d) = (c, d)(a, b) = (a, b). (ac, ad + b) = (ca, cb + d) = (a, b). Эти равенства выполняются при c = 1, d = 0. Значит, единичный элемент e = (1, 0).
4. Обратный элемент: (a, b)(a, b) − 1 = (a, b) − 1(a, b) = (1, 0). (a, b)(c, d) = (c, d)(a, b) = (1, 0). (ac, ad + b) = (ca, cb + d) = (1, 0). Эти равенства выполняются при c = 1 / a , d = − b/ a . Значит, обратный элемент имеет вид (a, b) ^−1 = 1 / a , − b/ a .
Вывод, пары (a, b) вещественных чисел, a <> 0, составляют группу отно- сительно операции (a, b)(c, d) = (ac, ad + b).
Полная линейная группа векторного пространства V — это группа обратимых линейных операторов вида C: V → V[1]. Роль групповой операции играет обычная композиция линейных операторов.
В полной линейной группе GL(n, K) можно выделить подгруппу SL(n, K), состоящую из всех матриц порядка n с определителем, равным 1. Это — специальная линейная группа, обозначаемая SL(n, K).
Симметрической группой множества {\displaystyle X} называется группа всех перестановок {\displaystyle X} (то есть биекций {\displaystyle X\to X}) относительно операции композиции.
Подгруппа симметрической группы S(X) называется группой подстановок X.
4. Векторная алгебра.
Линейно зависимые и линейно независимые векторы.
Ненулевые
векторы 
называются линейно
независимыми,
если только тривиальная линейная
комбинация этих векторов равна нулевому
вектору.
Признаки коллинеарности и компланарности геометрических векторов. Разложение вектора на плоскости и в пространстве.
Базис на плоскости, в пространстве.
Координаты, действия с векторами в координатах.
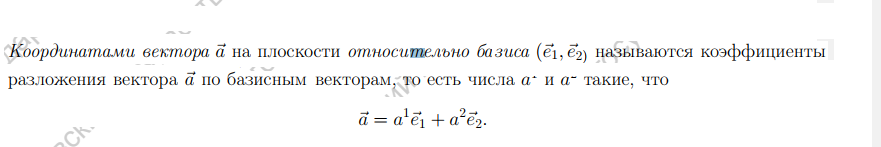
В
силу свойств
операций над векторами,
справедливы следующие равенства
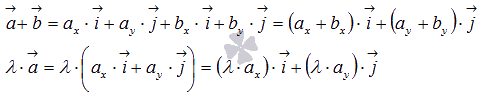
Правые
части этих равенств представляют собой
разложение векторов 
и 
по
координатным векторам 
и 
,
следовательно, векторы
и
имеют
координаты 
и 
соответственно.
Аналогично
для векторов 
и 
,
заданных в прямоугольной системе
координат Oxyz
Признаки коллинеарности и компланарности векторов в координатах.
Два вектора коллинеарны, если отношения их координат равны.
Вектора компланарны если среди них не более двух линейно независимых векторов.
Вектора компланарны, тогда и только тогда, когда их смешанное произведение равно нулю:
Радиус-вектор точки.
Деление отрезка в данном отношении.
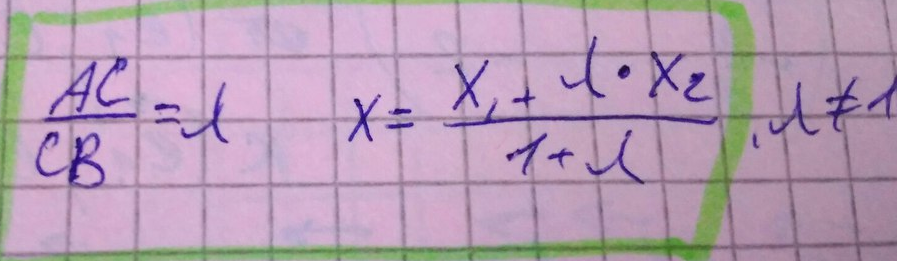
Численное значение проекции вектора на вектор.
Для вычисления проекции вектора a на направление вектора b из определения скалярного произведения получена формула:
Пр ba = |
a · b |
|b| |
(вектор а* вектор б(скаляр умн.)/длину вектора б)
Скалярное произведение векторов и его свойства.
Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов умноженного на косинус угла между ними:
a · b = |a| · |b| cos α (геом.)
Скалярным произведением двух векторов a и b будет скалярная величина, равная сумме попарного произведения координат векторов a и b. (алг.)
Выражение скалярного произведения в координатах.
В случае пространственной задачи скалярное произведение векторов a = {ax ; ay ; az} и b = {bx ; by ; bz} можно найти воспользовавшись следующей формулой:
Вект(a) · вект(b) = ax · bx + ay · by + az · bz
или
a · b = ax · bx + ay · by
Применение скалярного произведения в геометрии.
Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов умноженного на косинус угла между ними:
a · b = |a| · |b| cos α
Отношение одинаковой ориентированности на множестве базисов плоскости/пространства геометрических векторов.
Базис ( 1,2,3) называется одинаково ориентированным (1,2,3) если матрица перехода имеет положительный определитель.
Отношение одинаковой ориентированности называется отношением эквивалентности
Ориентированная плоскость и ориентированное пространство.
Чтобы задать ориентацию на плоскости (в пространстве) надо зафиксировать какой-нибудь базис , при этом зафиксированный базис называется положительным
Операции векторного и смешанного умножения в ориентированном пространстве и их свойства.
5. Кольца и поля.
Основные определения.
Кольцо вычетов по модулю n.
Условия, при которых кольцо вычетов является полем.
Характеристика поля.
Понятие изоморфизма алгебраических структур, основные примеры. Подкольца и подполя.
Отображение
(функция) 
называется
сюръективным (или сюръекцией, или
отображением на 
),
если каждый элемент множества
является
образом хотя бы одного элемента
множества 
,
то есть 
.
Отображение
(функция) 
множества
в
множество 
называется
инъекцией (или вложением, или взаимно
однозначным отображением множества
в
множество
),
если разные элементы множества
переводятся
в разные элементы множества
, 
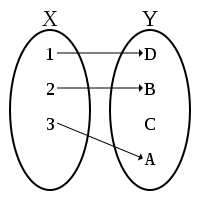Биекция
— это отображение (функция), которое
является одновременно и сюръективным,
и инъективным.
Поле комплексных чисел.
Теорема о существовании и единственности поля комплексных чисел.
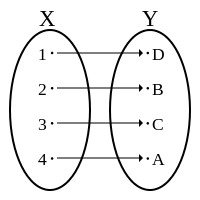
Тригонометрическая форма представления комплексного числа.
Формула Муавра.
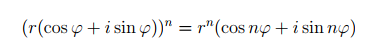
Извлечение корней из комплексного числа.
Определение алгебры над произвольным полем.
Основные примеры: алгебра геометрических векторов, алгебра матриц, алгебра кватернионов.
Кватернио́ны (от лат. quaterni, по четыре) — система гиперкомплексных чисел, образующая векторное пространство размерностьючетыре над полем вещественных чисел
2. Аналитический метод
6. Системы координат.
Векторные и арифметические системы координат: векторная система координат с данным полюсом, аффинные и декартовы системы координат, полярная, сферическая и цилиндрическая системы координат.
Аффинная система координат (косоугольнаясистема координат) — прямолинейная система координат в аффинном пространстве.
пара перпендикулярных прямых задает на плоскости декартову систему координат.
Сферическими
координатами называют систему
координат для
отображения геометрических свойств
фигуры в трёх измерениях посредством
задания трёх координат
Цилиндрической системой координат называют трёхмерную систему координат, являющуюся расширением полярной системы координат путём добавления третьей координаты
Полярная система координат — двухмерная система координат, в которой каждая точка на плоскости однозначно определяется двумя числами — полярным углом иполярным радиусом
Формулы преобразования систем координат.
7. Аналитическое решение простейших геометрических задач.
Вектор, определяемый двумя точками.
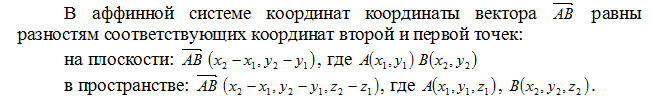
Расстояние между двумя точками.
Деление отрезка в данном отношении.
Площадь треугольника.
Объем тетраэдра.
8. Прямая на плоскости.
Основная теорема о прямой на плоскости.
Основные виды уравнений прямой на плоскости.
Взаимное расположение прямых на плоскости.
Угловой коэффициент прямой на плоскости.
Угол между прямыми на плоскости.
Расстояние от точки до прямой на плоскости. Пучок прямых на плоскости.
9. Плоскость и прямая в пространстве.
1) Основная теорема о плоскости в пространстве.
2) Исследование общего уравнения плоскости.
3) Взаимное расположение плоскостей в пространстве.
4) Расположение точек относительно плоскости в пространстве.
5) Основные виды уравнений плоскости в пространстве в аффинных и декартовых координатах.
6) Основная теорема о прямой в пространстве.
7) Условие параллельности вектора и прямой в пространстве.
Основные виды уравнений прямой в пространстве в аффинных и декартовых координатах.
Взаимное расположение двух прямых, прямой и плоскости в пространстве.
Угол между прямыми в пространстве, между плоскостями и между прямой и плоскостью.
Расстояние от точки до плоскости и прямой в пространстве.
Кратчайшее расстояние между скрещивающимися прямыми.
