ФГБОУ ВПО «Воронежский государственный технический университет»

А.Г. Остапенко А.В. Ряжских

А.Н. Шелковой Н.А. Ююкин

Основы теории графов

Утверждено Редакционно-издательским советом университета в качестве учебного пособия

Воронеж 2013

УДК 519.617 (075.8)

Основы теории графов: учеб. пособие [Электронный ресурс]. – Электрон. текстовые, граф. данные (6,3 Мб) / А.Г. Остапенко, А.В. Ряжских, А.Н. Шелковой, Н.А. Ююкин. – Воронеж : ФГБОУ ВПО «Воронежский государственный технический университет», 2013. – 1 электрон. опт. диск (CD-ROM). – Систем. требования: ПК 500 и выше ; 256 Мб ОЗУ ; Windows XP ; MS Word 2007 или более поздняя версия ; 1024x768 ; CD-ROM ; мышь. – Загл. с экрана. – Диск и сопровод. материал помещены в контейнер 12x14 см.

Настоящее учебное пособие состоит из пяти глав: первая глава посвящена способам задания графов, операциям над графами, метрическим характеристикам графов, во второй главе рассматриваются методы нахождения минимальных и максимальных путей на орграфах, в третьей главе – остовы графов, фундаментальные циклы, эйлеровы и гамильтоновы графы, доминирующие множества и клики, в четвёртой и пятой главах рассматриваются планарные графы и потоки в сетях.

Издание соответствует требованиям Федерального государственного образовательного стандарта высшего профессионального образования по специальности 090303 «Информационная безопасность автоматизированных систем», дисциплине «Теория графов и её приложения».

Табл. 3. Ил. 72. Библиогр.: 23 назв.

Рецензенты: кафедра высшей математики Воронежского

института МВД России (начальник кафедры

д-р физ.-мат. наук, проф. В.В. Меньших);

канд. техн. наук, доц. М.И. Бочаров

 Остапенко А.Г., Ряжских А.В., Шелковой А.Н.,

Ююкин Н.А., 2013

 Оформление. ФГБОУ ВПО «Воронежский

государственный технический университет», 2013

Введение

Это учебное пособие написано на основе лекций, читаемых авторами на факультете информационных технологий и компьютерной безопасности ВГТУ по курсам «Теория графов и её приложения» и «Дискретная математика».

В пособии изложены необходимые основы математического аппарата и примеры его использования: способы задания графов, операции над графами, метрические характеристики графов, упорядочивание элементов орграфов, нахождение минимальных и максимальных путей на орграфах, остовы графов, фундаментальные циклы, эйлеровы и гамильтоновы графы, доминирующие множества и клики, планарные графы, потоки в сетях. Такой объём знаний актуален сегодня для студентов, получающих образование по специальностям в области защиты информации, и соответствует требованиям государственных стандартов по этим специальностям.

Изложение материала проведено почти без доказательств – основной упор сделан на приобретение навыков использования математического аппарата. Каждый раздел сопровождается решением характерных задач. Пособие содержит также подборку вопросов для повторения, задач и упражнений для самостоятельного решения по каждой теме.

Глава 1. Способы задания графов. Операции над графами. Метрические характеристики графов. Упорядочивание элементов орграфов

1. Способы задания графов. Операции над графами. Метрические характеристики графов

1. Основные понятия и определения

Пусть S – непустое множество, V² – множество всех его двухэлементных подмножеств, U лежит в V². Тогда G=(S,U) называется неориентированным графом. Элементы множества S вершинами графа, а элементы множества U – рёбрами.

Если в паре вершин x_i и x_j указано направление связи, т.е. какая из вершин является первой, то соединяющий их отрезок U_k называется дугой, а вершины, определяющие дугу U_k – концевыми вершинами. Если концевые вершины совпадают то дуга называется петлёй. В графе G могут существовать дуги (рёбра) с одинаковыми концевыми вершинами. Такие дуги называются параллельными или кратными.

Если в графе G=(S,U) все элементы множества U изображаются дугами, то граф называется ориентированным или орграфом. Два ребра называются смежными, если они имеют общую концевую вершину. Вершины называются смежными или соседними, если есть ребро, их соединяющее.

Вершины x_i и ребро u_i называются инцидентными, если x_i является концевой вершиной ребра u_i, и неинцидентным в противном случае.

Число вершин графа называется его порядком. Число дуг (рёбер) графа G, инцидентных данной вершине, называется степенью P(x_i) вершины x_i. Если степень равна 0, то вершина называется изолированной, а если 1- то висячей или тупиковой.

Пример неориентированного графа.

X₇

Рис. 1

Множество вершин S={ x₁;x₂;x₃;x₄;x₅;x₆;x₇}.

Множество ребер U={ (x₁ x₁);(x₁x₂);(x₂x₃);(x₃x₄);(x₃x₅); (x₄x₅);(x₅x₆)}.

(x₁ x₁) – петля, x₇ - изолированная вершина, P(x₇)=0;

x₆ – висячая вершина, P(x₆)=1; P(x₂)=2; P(x₃)=3; P(x₄)=2; P(x₅)=3; P(x₁)=3; (ребро (x₁ x₁) учитывается дважды).

Граф G называется простым, если он не содержит дуг и параллельных дуг. Простой граф, в котором каждая пара вершин смежная, называется полным. Граф, содержащий хотя бы две параллельные дуги называется - мультиграфом; граф содержащий петли – псевдографом.

Граф называется двудольным, если существует такое множество разбиение его вершин на две части, что концы каждого ребра принадлежат разным частям. Если при этом любые две вершины, входящие в разные доли, смежны, то граф называется полным двудольным. Полный двудольный граф, доли которого состоят из p и q вершин, обозначается K_p,q. Полный граф порядка n обозначается K_n.

K₁

K₂

K₃

K₄

K_1,4

K_3,3

Рис. 2

Число рёбер в полном графе порядка n равно .

Два графа называются изоморфными, если между множествами их вершин существует такое взаимно – однозначное свойство, в котором в одном из графов ребрами соединены в том и только в том случае, если в другом графе ребрами соединены те же вершины. Для изоморфных орграфов ориентация также должна быть одинакова.

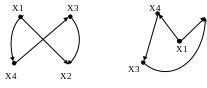
Рис. 3

Г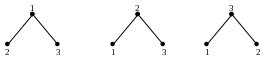 раф называется помеченным, если его вершинам присвоены некоторые метки, например 1, 2, 3, … .

Рис. 4

Число q_n непомеченных графов порядка n определяется формулой Пойа.

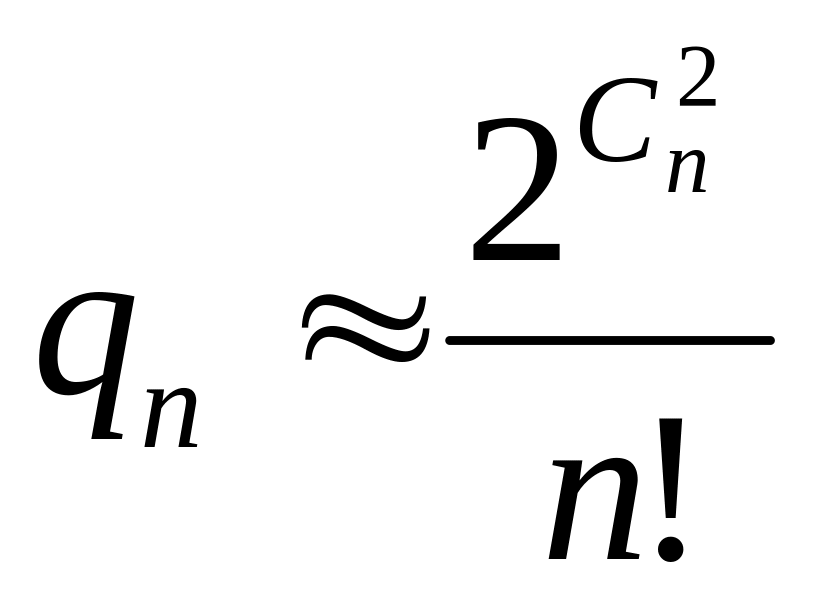
Она определяет лишь асимптотику числа q_n , т.е.

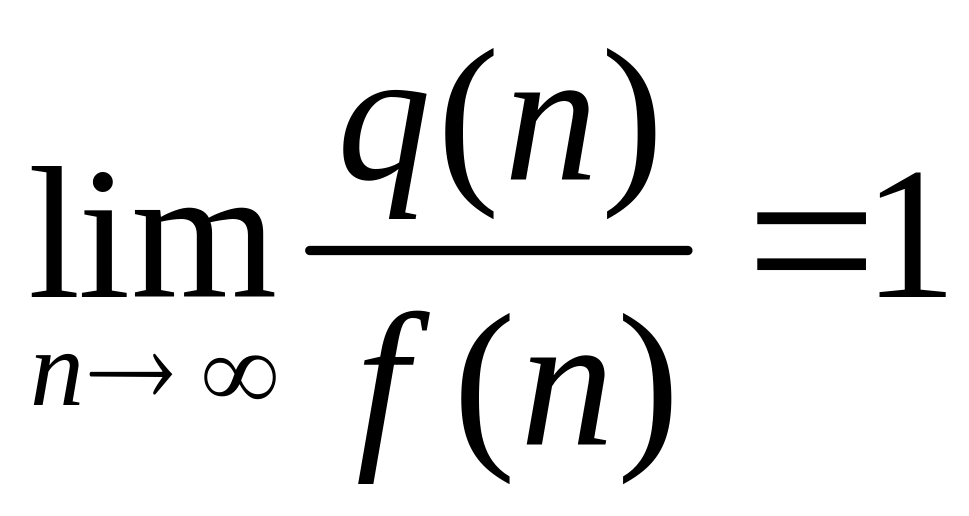, где q(n)=q_n, f(n)= .

Граф называется плоским, если он может быть изображён на плоскости так, что все пересечения его рёбер являются вершинами.

Дополнительным графом G’=(S,U’) к произвольному графу G=(S,U) называется граф, у которого вершин столько же сколько в графе G, причем любые две несовпадающие вершины смежны тогда и только тогда, когда они не смежны в G.

Рис. 5

Граф, изоморфный своему дополнению называется самодополнительным.

Граф называется подграфом графа G=(S,U) если и .